一类具有垂直传播的疟疾模型的渐近性态

葛 静

(淮阴师范学院 数学与统计学院，江苏 淮安 223300)

0 引言

疟疾是经受感染的雌性按蚊叮咬或输入带疟原虫者的血液而感染疟原虫所引起在人群中传播的虫媒传染病。雌性按蚊为了产卵的需要，它需要通过叮咬人类获得血液.在获得血的过程中，雌性按蚊可能获得从感染人类向蚊子传递的寄生虫，或者获得从蚊子向易感的或者已经感染的人群传递的寄生虫.所以，疟原虫的寄生虫有一个复杂的传播过程，涉及到人和蚊子，是一种媒介传染病.根据《 2018年世界疟疾报告》，自2001年以来，大规模的疟疾干预措施已帮助挽救了约700万人的生命。但是，估计仍有32亿人处于危险之中，仅2018年，全世界估计发生了2.28亿疟疾病例，有405 000人死亡，其中大多数是撒哈拉以南非洲5岁以下的儿童死亡。因此有必要采取有效的防控措施抑制疟疾的流行，使得疾病的危害和损失降到最低.数学上对传染病的研究主要通过建立反映传染病动力学特征的模型，并对模型动力学性态进行定性、定量分析来揭示疾病的发展过程、流行规律，从而预测其发展流行趋势，寻求预防和控制的最优策略.

最早用来进行疟疾研究的数学模型是Ross-MacDonald数学模型仅仅包含感染宿主人群和感染媒介蚊子之间的相互影响[1-4].近些年，在Ross-MacDonald的工作基础上，越来越多的科研工作者考虑了不同的因素，构建了多种形式的疟疾模型,从不同角度探讨疾病的动力学性态[5-8].

在文[9]中，作者探讨蚊帐和喷洒农药对疟疾传播的影响，研究了如下的疟疾模型:

(1)

其中在t时刻处的人总量为Nh(t)，即Nh(t)=Sh(t)+Ih(t)+Rh(t).同样，在t时刻处蚊子总量为Nm(t)，其被分为易感蚊子类Sm(t)和感染蚊子类Im(t)，即Nm(t)=Sm(t)+Im(t).模型(1)以及下文中所涉及的变量和系数的解释参见表1.

表1 数学模型中变量和系数的生物学定义

1 模型的建立

本文忽略外在防蚊工具和药物的影响，主要考虑垂直传播的影响，研究如下疟疾传播系统:

(2)

其中q表示病毒在蚊子中的垂直传播率，rm表示成熟蚊子的再生率，先进行无量纲化,设

假设成熟蚊子的再生率和新增率相同，即rm=λm.易知闭集:

D={(sh,ih,rh,sm,im)∈R5:0sh,ih,rh,sv,iv1,sh+ih+rh=1,sm+im=1},

是问题(2)的正不变集.注意到sh+ih+rh=1，sv+iv=1，则模型(2)可以简化成如下形式:

(3)

其中α=bmαhm,γ=bmαmh.

利用下一代矩阵的方法[10]，可以计算出模型(3)的基本再生数R0为:

注：从基本再生数R0的表达式可知垂直传播率越高，R0就越大，疾病传播的风险越高.

2 稳定性分析

易知系统(3)有无病平衡点E0=(1,0,0)，先讨论无病平衡点的局部稳定性.

定理1 当R0<1时，系统(3)的无病平衡点E0=(1,0,0)是局部稳定的；当R0>1时，系统(3)的无病平衡点E0=(1,0,0)是不稳定的.

证明在E0=(1,0,0)处对系统(3)进行线性化得相应的线性系统的系数矩阵为:

其相应的特征方程为:

所以两个特征根的实部Re(λ)<0，故由Routh-Hurwitz法则可知：当R0<1时系统(3)在E0处是局部渐近稳定的，当R0>1时，系统(3)的无病平衡点E0是不稳定的[11].

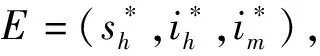
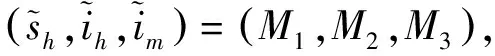
(4)

(5)

当ε充分小时，为使式(5)成立，只要下式成立，

(6)

整理得:

(7)

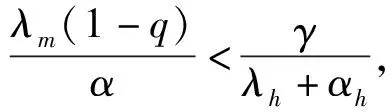
K1=λh+2βh+γ，K2=γ+λh+αh，K3=α+λm(1-q)，

再以

作为初始值，通过以下迭代过程

再由单调有界定理得极限

存在，且满足

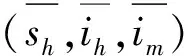
(8)

因此由单调迭代动力系统理论[12]可知，对于任意给定的初值(sh(0),ih(0),im(0))，如果(0，0，0)≤(sh(0),ih(0),im(0))≤(1,1,1)，则系统(3)的解(sh(t),ih(t),im(t))满足

3 结论

通过建立一种具垂直传播的疟疾模型并进行理论分析，得到如下结论：当垂直传播率足够高使得基本再生数大于1时，疟疾病毒仍将持续蔓延，导致地方病的出现；当垂直传播率较小且基本再生数小于1时，疟疾病毒将逐渐消失，疾病得以控制.为此一些国家和地区(例如广州)目前采取的方法是释放携带沃尔巴克体的雄蚊，让白纹伊蚊“绝育”，达到减少垂直传播的概率，有利于降低疟疾传播的基本再生数，从而达到控制疟疾病毒蔓延的目的.