开放、探索问题

一、填空题

1.（2019年盐城部分学校联考）设α∈，则使函数y=xα的定义域为R且为奇函数的所有α的值为________________.

3.如图，A，B，C，D为空间四点，在△ABC中，.正三角形ADB以AB为轴运动.当CD=_______时，CD⊥平面ABC.

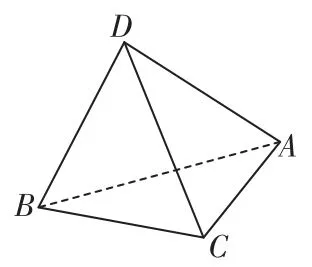
（第3题）

4.（2020年连云港市模拟卷）在△ABC中，已知则cosC的最小值是________.

5.若用长度分别为1，1，1，1，x，x的六根笔直的铁棒，通过焊接其端点（不计损耗）可以得到两种不同形状的三棱锥形的铁架，则实数x的取值范围是________.

6.对于数列｛an｝，定义数列｛Δan｝满足：Δan=an+1-an（n∈N*），定义数列｛Δ2an｝满足：Δ2an=Δan+1-Δan（n∈N*），若数列｛Δ2an｝中各项均为1，且a21=a2010=0，则a1=________.

7.设无穷数列｛an｝具有以下性质：①a1=1；②当n∈N*时，an≤an+1.请给出一个具有这种性质的无穷数列｛an｝，使得不等式对于任意的n∈N*都成立：_______.

9.在△ABC中，AC=6，BC=7，cosA=，0是△ABC的内心，若，其中0≤x≤1，0≤y≤1，动点P的轨迹所覆盖的面积为________.

10.（2020年常州市模拟卷）设数列｛an｝的前n项和为Sn，且，若对于任意的n∈N*都有1≤x（Sn-4n）≤3恒成立，则实数x的取值范围是________.

二、解答题

11.已知抛物线C：y2=2px（p＞0）上任意一点到其焦点F的距离比到y轴的距离大1.

（1）求抛物线C的方程；

（2）若过点F的直线交抛物线于M，N两点，M在第一象限，且|MF|=2|NF|，求直线MN的方程；

（3）求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题.例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”.求出体积为后，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体积为，求该正四棱锥的侧棱长”；也可以是“若正四棱锥的体积为，求其所有侧面面积之和的最小值”.

12.（2020年西安市模拟卷）在平面直角坐标系x0y中，已知椭圆T的方程为y2=1.设A，B，M是椭圆T上的三点（异于椭圆顶点），且存在锐角θ，使.

试探究下列各个量是否为定值；若是，请求出定值，否则，请说明理由：

（1）直线0A与0B的斜率之积；

（2）0A2+0B2.

13.设｛an｝是各项均为正整数的无穷数列.记a1，a2，…，ak（k∈N*）中的最大项为Mk，ak+1，ak+2，…中的最小项为mk.

（1）若mk-Mk=1，问：｛an｝是否为等差数列？若是，请给出证明；若不是，请说明理由；

（2）若｛an｝是等比数列，且公比q≠1，求mk-Mk的最小值.