平面几何中的平面向量数量帜问题
2020-07-16
一、填空题
1.(2019年嘉兴模拟题)已知单位向量e1与e2的夹角为α,且,向量a=3e1-2e2与b=3e1-e2的夹角为β,则cosβ=________.
2.△A0B为等腰直角三角形,0A=1,0C为斜边AB的高,点P在射线0C上,则的最小值为________.
3.已知a,b为平面向量,若a+b与a的夹角为,a+b与b的夹角为,则________.
4.(2019年扬州中学模拟题)设四边形ABCD为平行四边形,若点M,N满足,则=________.
6.已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则的值为________.
7.(2020年济南市模拟题)已知点0是△ABC的外心,AB=AC=2,若,且x+2y=1,则△ABC的面积等于________.
8.(2020年合肥市模拟题)在矩形ABCD中,,点F是CD的中点,点P在边AD上,则的最小值是________.
9.设向量a,b,c满足|a|=|b|=1,a·,则|c|的最大值为________.
10.(2020年上海杨浦区期末卷)设平面内的向量(2,1),点P是直线0M上的一个动点,求当取最小值时,∠APB的余弦值为________.
二、解答题
11.如图,在四边形ABCD中,E为AC的中点.
(1)若cos∠ABC,求△ABC的面积S△ABC;

(第11题)

12.(2019年常州中学月考题)在矩形ABCD中,,N是CD的中点,M是线段AB上的点,|a|=2,|b|=1,
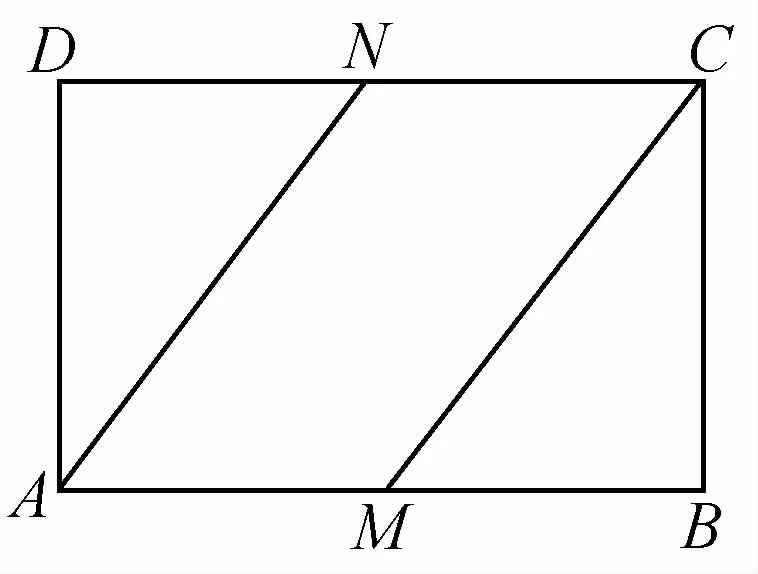
(第12题)
(1)若M是AB的中点,求证:与共线;
(2)在线段AB上是否存在点M,使得与垂直?若不存在,请说明理由,若存在,请求出M点的位置;
(3)若动点P在矩形ABCD上运动,试求的最大值及取得最大值时P点的位置.

13.如图,正方形ABCD边长为2,内切圆为⊙0,点P是⊙0上任意一点.
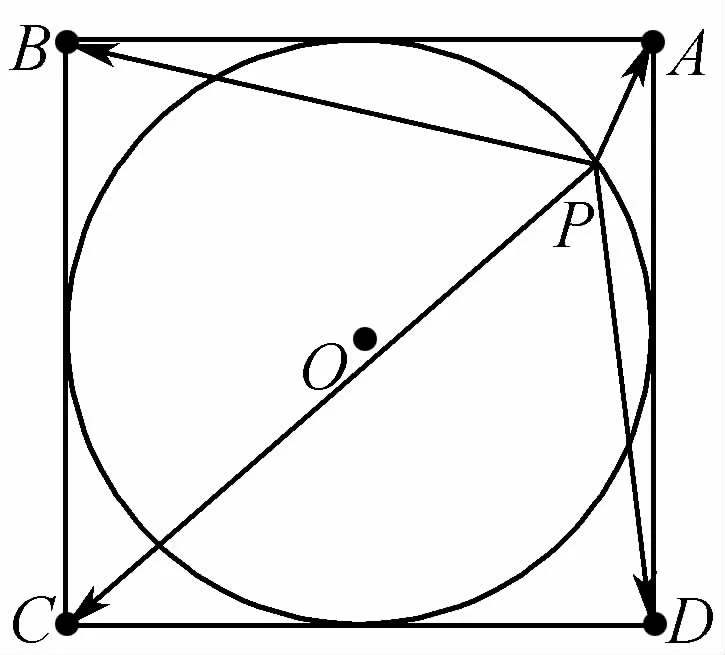
(第13题)

14.在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°.动点E和F分别在线段BC和DC上,且,求的最小值.

