可控中子源密度测井仪的密度响应特性与算法研究

岳爱忠，陈海铮，张清民,*，高可庆，张晓蕾，孙培伟,，王树声，赵媛媛，王 虎

(1.中国石油集团测井有限公司 技术中心，陕西 西安 710077；2.西安交通大学 核科学与技术学院，陕西 西安 710049；3.西安交通大学 核电厂与火电厂系统国家级虚拟仿真实验教学中心，陕西 西安 710049)

在石油勘探与开发过程中，密度测井是一种普遍又非常重要的测井方式，它主要是利用γ射线与地层物质发生的康普顿效应来测量地层密度。传统密度测井利用137Cs源作为γ源，利用其放出的能量为0.662 MeV的γ射线在地层中与地层物质发生康普顿效应，再通过测井仪器上的γ探测器对衰减后的γ射线强度进行测量，从而得到地层密度相关信息。

传统密度测井中放射性γ源的危害[1]一直受到人们的关注。传统的密度测井仪不仅采用有安全隐患的放射性同位素源，而且，其功能也较单一，因此在多重评价体系的地层勘探开发过程中需采用多个测井仪分别进行检测，大幅降低了测井效率。利用可控中子源代替放射性同位素源，既可减小辐射风险，又可增加测量的可靠性。随着健康、安全、环保(HSE)测井理念的提出，可控脉冲中子源替代传统化学源已是核测井的发展趋势。

20世纪90年代以来，脉冲中子测井得到飞速发展，主要是在油田生产开发过程中，用于在套管井内确定储层饱和度、监测储层，近年来开始应用于地层元素[2]和地层密度[3]测井。如康普乐公司发布的脉冲中子衰减能谱测井仪(PND-S)提供了利用快中子非弹性散射产生的γ射线求取密度孔隙度的简化方法[4-5]；哈里伯顿公司推出的脉冲中子俘获测井仪(PNC)利用非弹性计数率(RINC)校正法结合回归技术预测地层密度，之后又开发了利用神经网络群(NNE)将PNC测量结果直接转换成地层密度的NNE方法[6-7]；斯伦贝谢公司推出了包括脉冲中子密度测井在内的随钻测井平台EcoScope，利用测量快中子的衰减来对次生γ源的强度进行校正，然后通过同时测量超热中子和γ射线的强度来确定地层的密度[8-9]。而国内的相关研究起步晚，其中于华伟等[10-11]对非弹性散射扩散长度法进行了改进，并研究了其在随钻环境中的测量效果，之后还对核测井模拟所采用的MCNP程序进行了优化，改进了模拟精度，并建立了使用超热中子计数校正γ源分布对远探测器非弹性散射计数率影响的密度测井模型。

目前，中国石油集团测井有限公司正在研究制造一种可控中子源一体化测井仪，以完成对多个地层参数的有效测量，如地层元素含量、地层密度、孔隙度以及地层水矿化度等信息。由于脉冲中子源的中子产额存在波动，采用探测器绝对计数的密度算法受地层环境、测量条件的影响较大，导致密度算法的精度较差[12]。为对这种新型测井装备研制提供理论指导，本文在对新型一体化测井仪进行蒙特卡罗建模分析的基础上，研究近、远γ探测器的非弹性散射γ计数和俘获γ计数，中子探测器的近热中子及近超热中子计数与地层密度之间的响应关系，建立一种适合该测井仪的密度算法。

1 一体化测井仪及MCNP建模

1.1 可控中子源测井原理

在可控中子源测井中，测井时氘-氚(D-T)中子发生器产生能量为14.1 MeV的快中子。当高能中子射入地层后，依次与地层元素发生非弹性散射、弹性散射及俘获反应，其中快中子的非弹性散射和热中子的俘获都会释放出γ射线，这些γ射线相当于γ-γ密度测井中的γ源。传统的同位素γ源的能量单一，且与探测器的距离基本固定，而可控中子源产生的次生γ源与之不同：首先，次生γ射线来源于中子与地层所有元素(如碳、氧、硅等)的相互作用，因此，次生γ源的能量不是单一的，会随地层元素组成而变化；其次，次生γ源也不是一个点源，而是一个空间分布源，其分布会随地层的原子密度及含氢指数等性质而变化，因此，次生γ源到探测器的距离(即源距)是不固定的。

在探测γ射线时，γ探测器所探测到的γ信号主要受2个因素影响：1) 快中子输运，其决定次生γ源的产生及分布；2) 次生γ射线的输运，与γ-γ测井相同，在输运中要经过康普顿散射、光电反应和电子对效应等[13]，强度逐步衰减。因此，探测器接收的γ计数对3个过程敏感：快中子衰减、γ射线产生和γ射线衰减。快中子衰减主导次生γ源最初的空间分布；对于γ射线的产生，介质的组成和密度决定产生γ射线的数量和能量；γ射线的衰减反映能到达探测器的γ射线产生范围。由于中子输运和γ射线输运的共同作用，使可控中子源密度测井测量地层密度的方法不同于传统的γ-γ密度测井。因此在新的密度算法中，需考虑使用能反映中子衰减的热中子计数、超热中子计数和由非弹性散射、辐射俘获产生的非弹性散射、俘获γ计数，从而得到准确的地层密度。

1.2 模型建立

可控中子源测井仪在MCNP中建模后得到的可视化剖面图如图1所示，该测井仪主要结构包括：脉冲中子源、近γ探测器、远γ探测器、近超热中子探测器、近热中子探测器、远热中子探测器和屏蔽体等。仪器模型的具体参数如下。

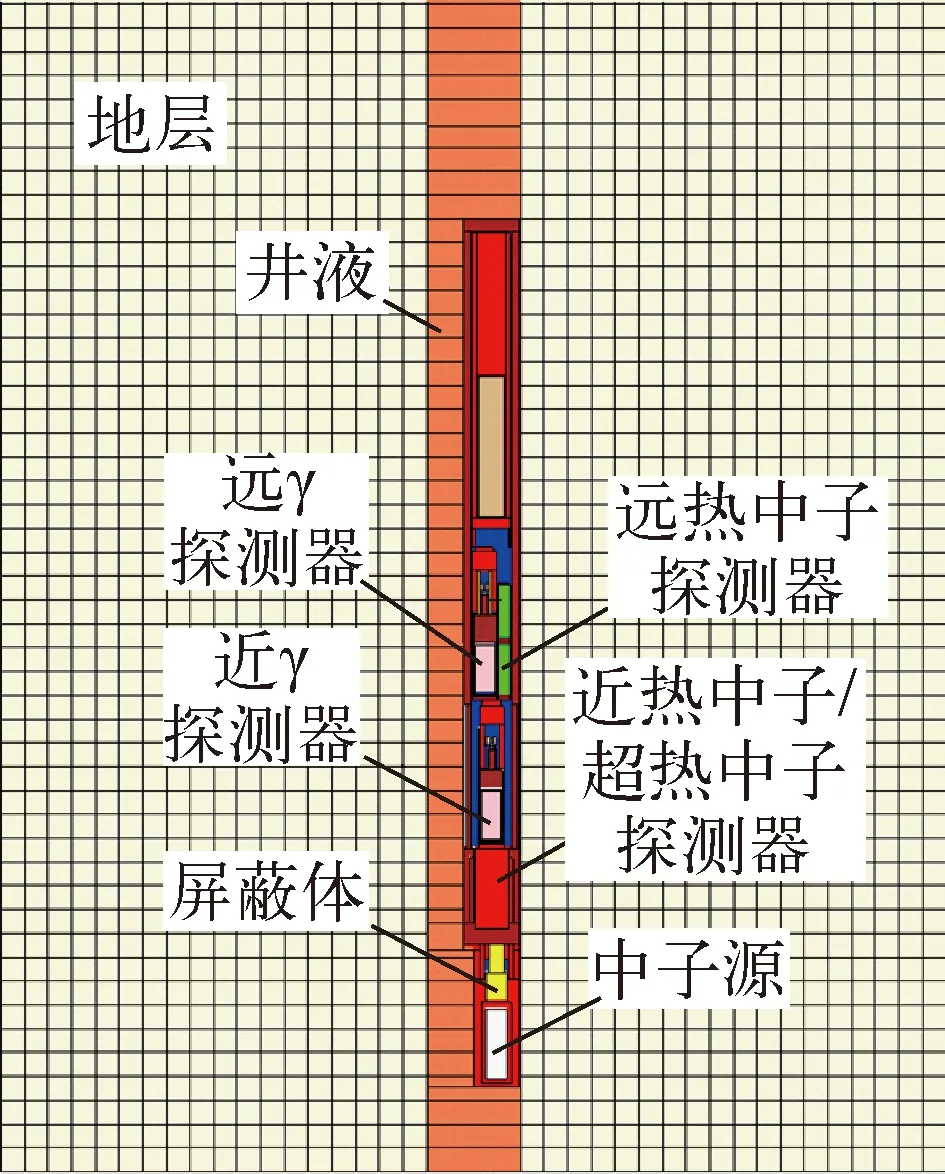
图1 可控源测井仪在MCNP中的可视化剖面图

1) 地层栅元划分及材料设置

根据模型井实际情况，建立圆柱型地层模型，其中，地层外径为180 cm，内径(井眼直径)为20 cm，井眼中包含井液和仪器，同时地层厚度为250 cm。为方便调试，地层模型在径向上分成18个同心圆柱环，在轴向上细化为50段，采用均匀划分。地层材料选取灰岩、白云岩和砂岩3种岩性的地层条件，并在每种岩性条件下从20%至100%每间隔5%选取21个不同孔隙度下的密度点，所获得的密度范围分别为：灰岩，1～2.703 g/cm3；白云岩，1～2.860 g/cm3；砂岩，1～2.641 g/cm3。

2) 井液

测井仪外壳与井壁之间是井液，测井仪靠井壁放置，井眼中充满水，并将井液也在轴向上分为50个部分。

3) 测井仪结构参数

中子源为半径11.5 mm的平面D-T源，各向同性均匀发射14.1 MeV快中子。为使可控中子源发射的高能中子尽可能不直接进入测井仪，在可控中子源正上方采用12.2 cm厚的镍钨铁合金屏蔽。

测井仪所用探测器的材料及尺寸列于表1。

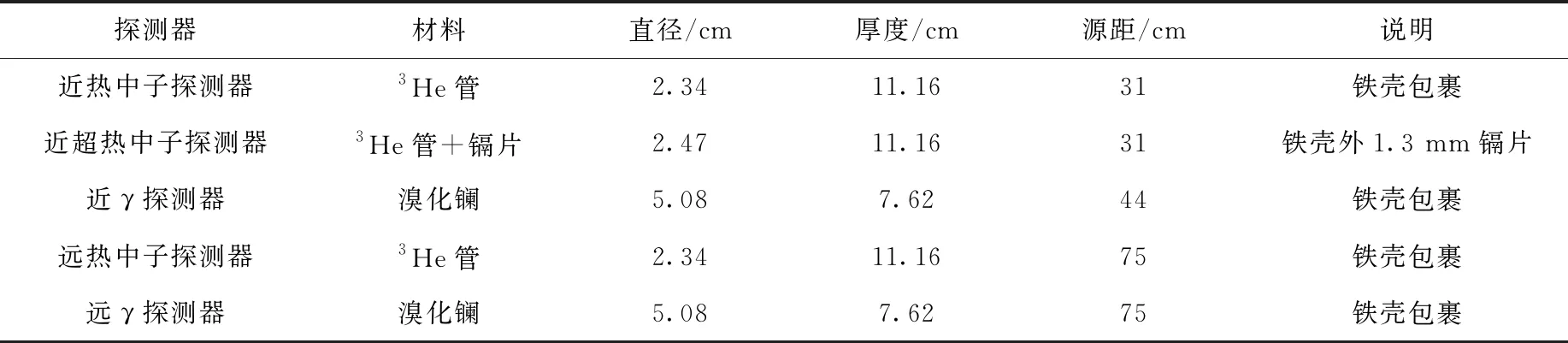
表1 测井仪所用探测器的材料及尺寸

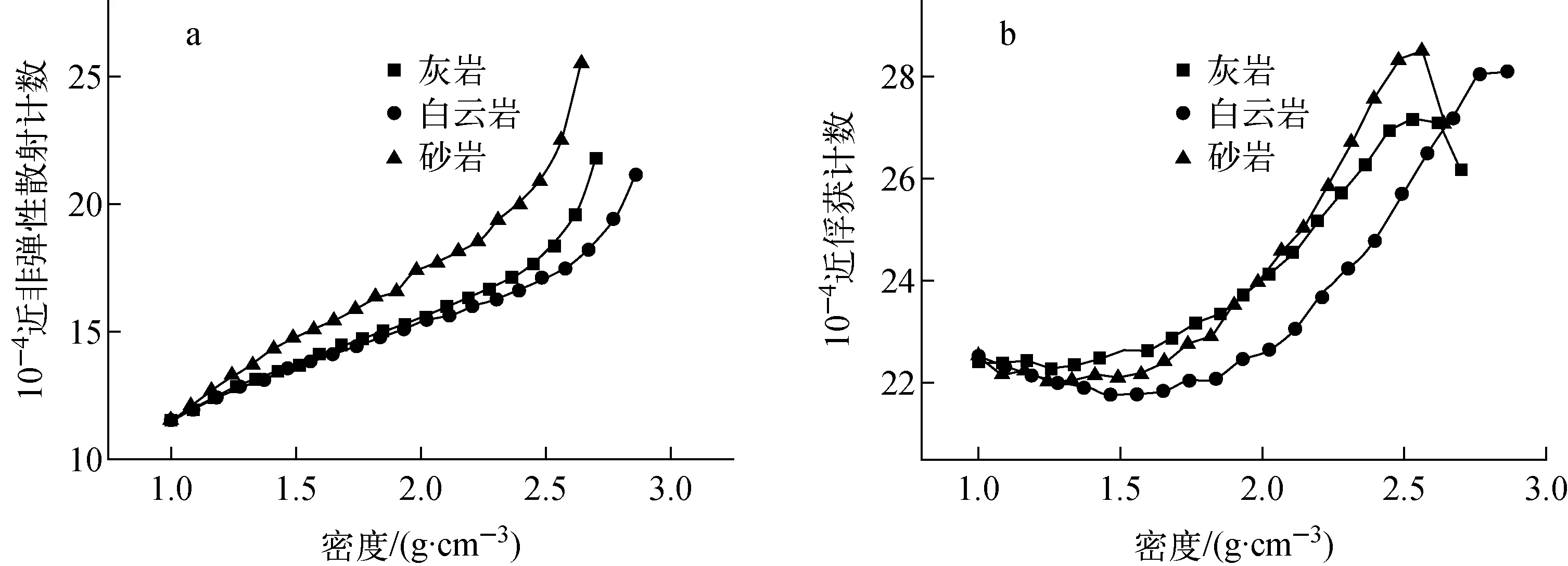
图2 近γ探测器非弹性散射γ计数和俘获γ计数的密度响应特性曲线

1.3 时间截断

由于地层中的γ射线主要有2个来源，因此需区分非弹性散射γ计数和俘获γ计数。脉冲中子源的脉冲宽度为40 μs，因为非弹性散射发生在中子发射之后的几十ns，所以使用MCNP程序中自带的cut：p卡片截断反应时间能实现非弹性散射和俘获γ射线的区分。计算俘获γ计数时截取时间间隔为50 μs～∞的能谱，计算非弹性散射γ计数时截取时间间隔为10～40 μs和50～80 μs的能谱，具体的计算表达式如下：

t俘获=t∞-t50

(1)

t非弹=t40-t10-m(t80-t50)

(2)

式中：不同下标的t表示不同的时刻；m为俘获组分在非弹性散射-俘获复合谱中的占比。因为截取时间间隔为10～40 μs的能谱中既有非弹性散射γ射线也有部分俘获γ射线，因此可通过减去相同时间宽度下仅包含俘获γ射线的50～80 μs时间段的能谱来得到纯净的非弹性散射谱。

2 数值模拟结果及分析

基于上述模型和时间截断方法得到的模拟结果，可绘制密度响应曲线。

1) 近γ探测器密度响应特性曲线

近γ探测器非弹性散射γ计数和俘获γ计数的密度响应特性曲线示于图2。从图2a可看出，在3种岩性条件下，近γ探测器的非弹性散射γ计数均随密度的减小呈下降趋势，这是因为随着地层密度的降低，地层孔隙度增大，其含氢量也增大。由于氢是良好的中子慢化剂，含氢量越高，中子减速越快，能量衰减也越快，而非弹性散射反应发生在中子辐射后的很短时间内，所以随着地层密度的减小，中子辐射瞬间更多的中子被慢化到非弹性散射的阈能之下，相应的发生非弹性散射反应的中子减少，所以在低密度情况下近γ探测器的非弹性散射γ计数较低，高密度时非弹性散射γ计数较高。但这种增长规律还与具体的岩性有关，在相同密度下砂岩的计数率高于灰岩和白云岩。由于γ射线在整个过程中所经历的已不是单一的γ输运过程，简单来说，至少要经历2个过程，即中子输运和非弹性散射γ输运，而这2个输运过程都受到具体介质性质的影响，即岩性的影响。

从图2b可看出，俘获γ计数的密度响应规律较非弹性散射γ计数的复杂，俘获γ计数基本是随密度的增加先减少后增加再减少。为定性分析俘获γ计数的密度响应规律，将俘获γ计数随密度的变化分为低密度和高密度2个阶段。在低密度段，地层的含氢量很高，地层中的水能在较短的距离内将足够多的快中子慢化为热中子，中子慢化长度随密度的变化较小[14]。同时地层中的矿物含量相对较少，而热中子主要与矿物元素发生反应产生俘获γ射线，所以在低密度段，随着密度的增加，含氢量减少，快中子的慢化迅速减弱，而地层矿物元素含量的增加并不显著，这就导致低密度段密度响应曲线下降。密度增加到一定程度后，矿物元素含量显著增加，快中子和矿物元素的弹性散射的反应概率也随之增大，一定程度上也会导致热中子含量的增加，再加上此时地层中矿物元素的含量很高，发生俘获反应的概率也会非常高，所以密度响应曲线会显著增高。在高密度段，地层含氢量大幅度下降，中子慢化长度随密度迅速增加，热中子与地层元素发生反应形成次生γ源的源距成为影响近γ探测器俘获计数的主要因素。次生γ源的源距大幅度上升导致探测器有效探测立体角减小，所以密度响应曲线在高密度段有下降的趋势。这与文献[14]是相符的。

2) 远γ探测器的密度响应特性曲线

远γ探测器的密度响应特性曲线示于图3。对比图3a与图2a可见，远γ探测器非弹性散射计数的密度响应曲线与近γ探测器的相似，同样是非弹性散射γ计数随密度的增大呈增长趋势，且密度响应也受到岩性的影响。但远γ探测器的响应曲线增长趋势在低密度区更加平缓，曲线上的小幅波动是因为所用测井仪中，近、远探测器的源距分别为44 cm和75 cm，在地层密度较低时，远探测器源距很大，因此远γ探测器的非弹性散射γ计数明显较少。

同样对比图3b与图2b可见，远γ探测器的俘获γ计数密度响应曲线与近γ探测器的差异不大，远γ探测器的曲线先降后升，这是因为对于远γ探测器，其次生γ源到探测器的源距很大，因此中子慢化长度的变化对探测器计数的影响不再重要，而导致远γ探测器俘获计数密度响应的主要影响因素与近γ探测器俘获计数密度响应的第1阶段一致。

3) 近热中子和近超热中子探测器计数的密度响应特性曲线

近热中子计数和近超热中子计数的密度响应特性曲线如图4所示，可见近热中子和近超热中子计数随密度的响应曲线较简单，基本符合中子输运的指数规律。

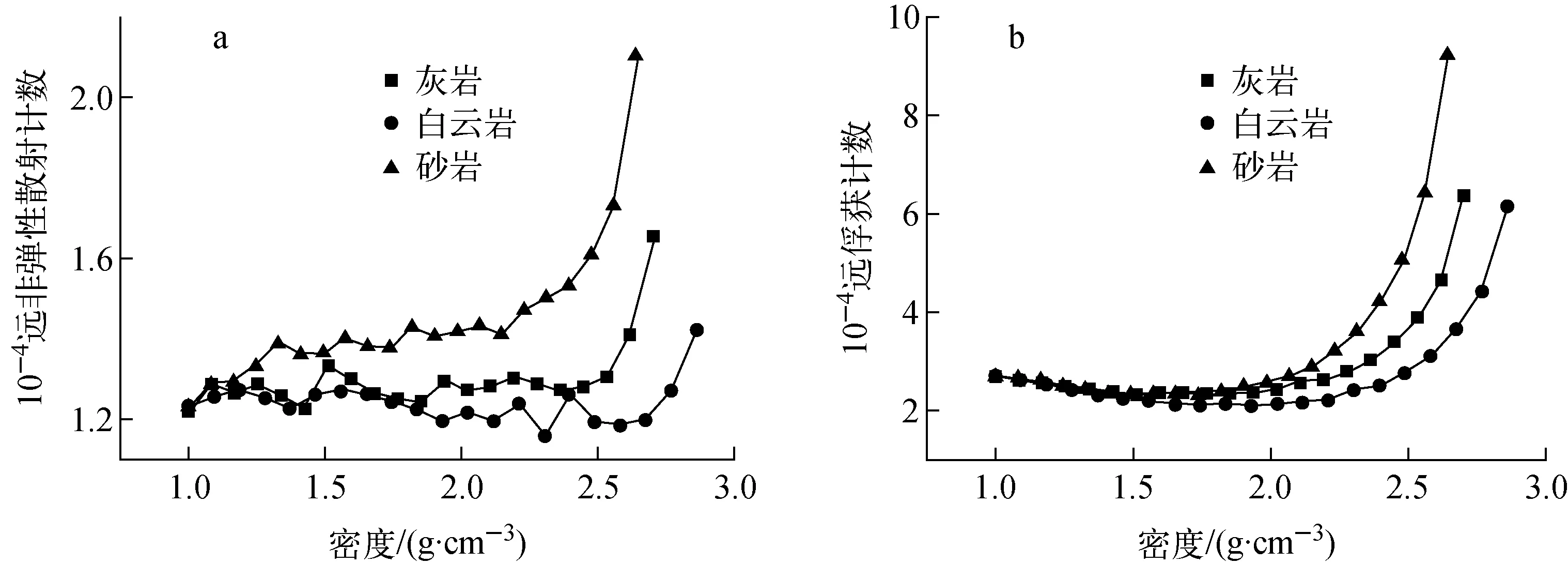
图3 远γ探测器非弹性散射γ计数和俘获γ计数的密度响应特性曲线

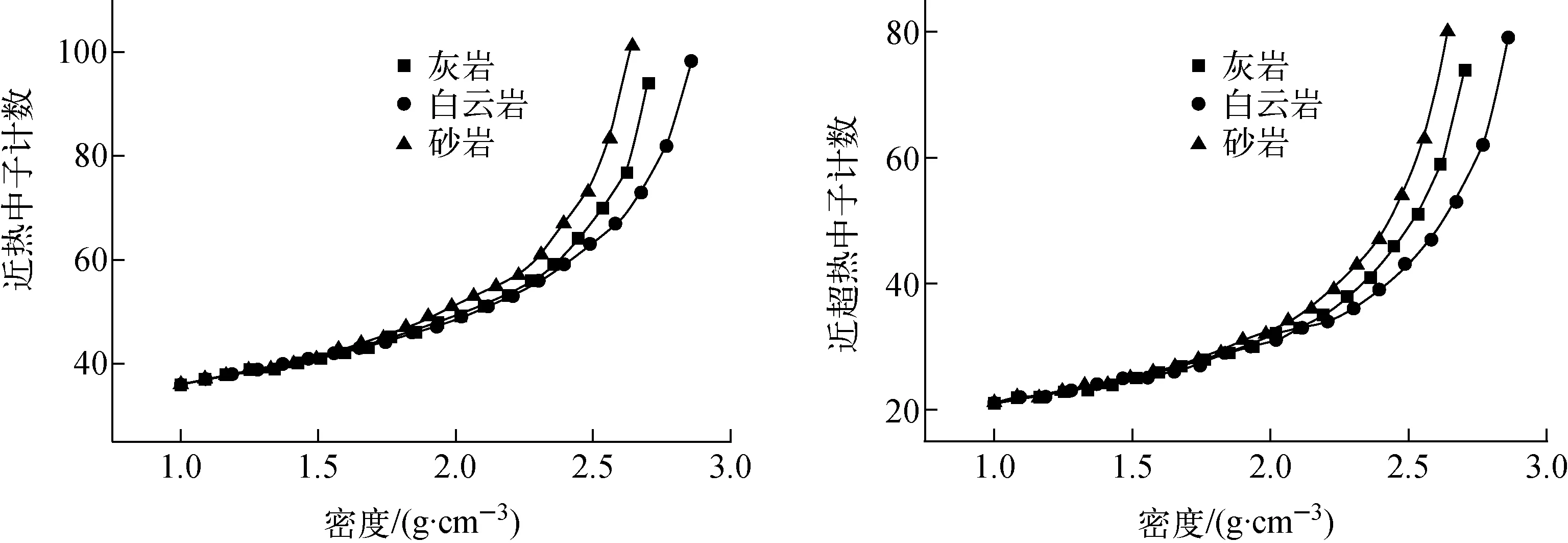
图4 近热中子和近超热中子探测器计数的密度响应特性曲线

3 密度公式拟合

通过前文关于利用可控中子源的γ密度测井原理以及响应特性可知，地层密度与γ计数、热中子以及超热中子计数的关系受诸多因素影响，这些因素限制了地层密度的测量，只有将相关因素予以校正，才能使密度测量关系变得简单。因此对MCNP的数值模拟结果进行了进一步分析，发现近俘获曲线对密度的响应不是单调的，所以设计算法时需规避俘获的影响。通过用近超热中子计数(Nepi)校正近远γ探测器非弹性散射γ计数比(Rine)发现，Rine与Nepi的比值取对数后与地层密度存在较好的线性响应关系，如图5所示。

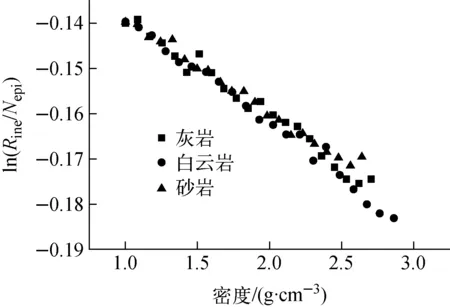
图5 ln(Rine/Nepi)密度响应曲线

从图5可看出，由近超热中子计数校正后的近远γ探测器的非弹性散射γ计数比与地层密度存在一定的线性响应关系，岩性的影响明显变小。同时在可控中子源密度测井中使用的脉冲中子源在不同脉冲下中子产额存在波动，会导致实际测井仪中探测器的绝对计数受测量条件影响很大。因此，选取近热中子计数Nth、近超热中子计数Nepi以及近远γ探测器非弹性散射γ计数比Rine作为密度拟合公式参数，可消除绝对计数带来的系统误差。利用模拟时设置的密度真值和模拟得到的上述探测器计数，采用式(3)进行曲线拟合可得到密度计算公式中的参数a=3.307 7、b=15.755 3和c=5.082 1。

(3)

利用模拟数据和式(3)可得到密度的计算值及误差。为便于分析比较，将真实密度和计算密度分别作为横、纵坐标绘图，如图6a所示，计算结果的相对误差如图6b所示。

从图6可看出，3种岩性下计算密度与真实密度非常接近，其相对误差均小于6%，这说明计算公式不依赖于岩性，已实现了岩性校正。且计算密度值和真实密度的相关性很高，R=0.997，说明计算公式达到了很高的精度。

为对比本文提出的密度算法与同行算法的差异，基于本模型模拟数据使用哈里伯顿以及斯伦贝谢的密度算法进行了计算，按哈里伯顿算法拟合的密度计算公式[12]为：

ρ=2.845 9×

ln(RIN-0.264 5×RNF-4.509 6)

(4)

其中：RIN为近远γ探测器非弹性散射γ计数比；RNF为近远γ探测器俘获计数比。

按斯伦贝谢算法拟合的密度计算公式[12]为：

(5)

其中，N远γ非弹为远γ探测器非弹性散射γ计数；N超热为近超热中子探测器计数。

由哈里伯顿算法和斯伦贝谢算法得到的密度与真实密度的关系如图7、8所示。

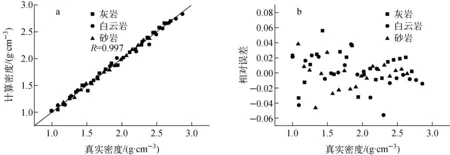
图6 本文算法的计算密度和真实密度的关系

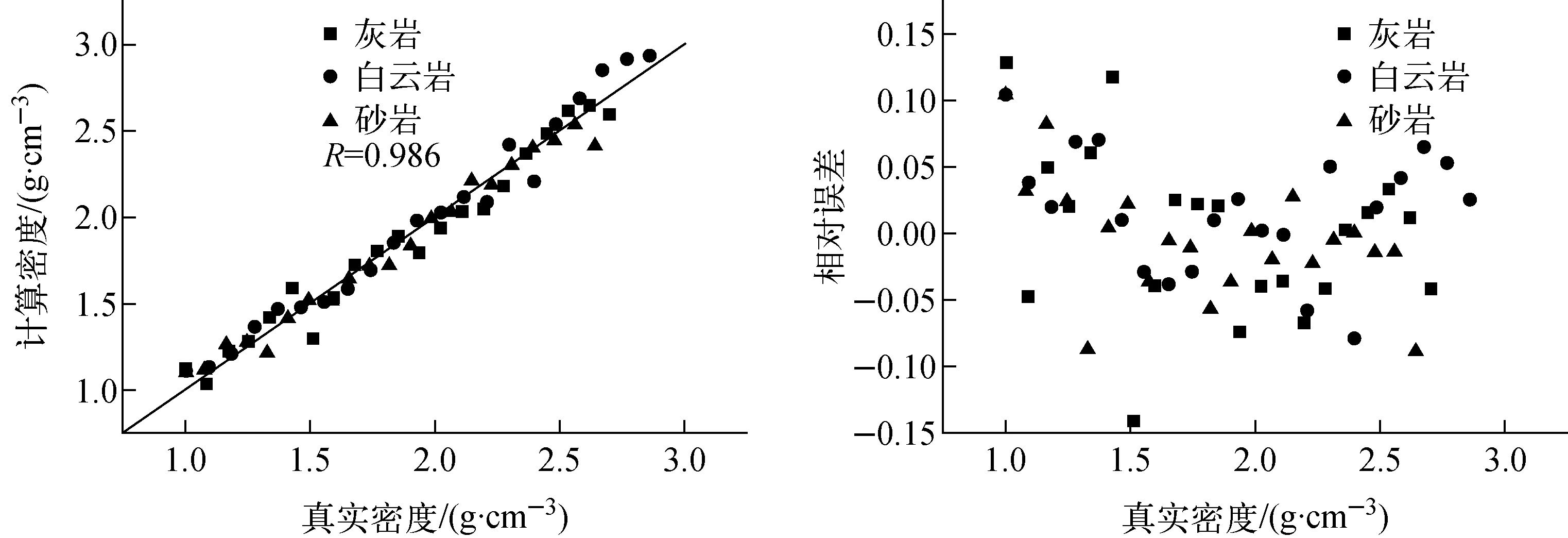
图7 哈里伯顿算法的计算密度与真实密度的关系

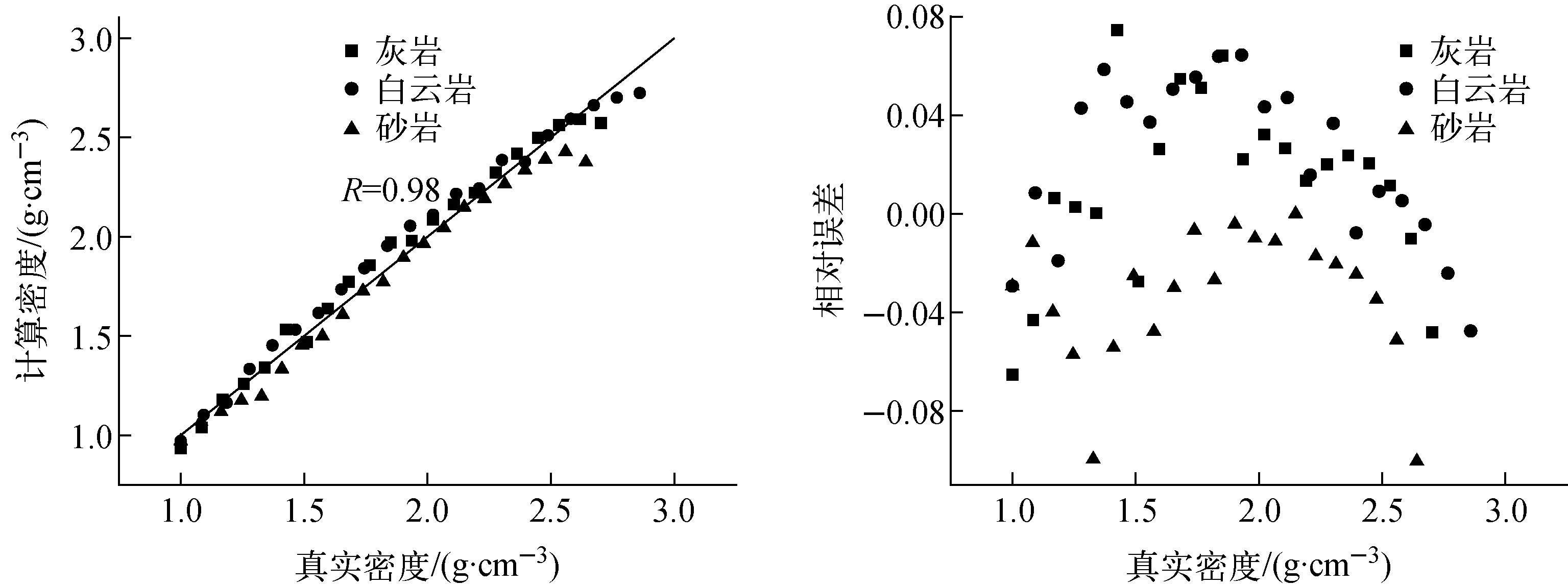
图8 斯伦贝谢算法的计算密度与真实密度的关系

通过对比图6～8可知，本文算法明显优于其他2种算法。尽管哈里伯顿算法对岩性校正已达到较好的程度，但其计算相对误差是本文算法的2倍左右，这表明本文算法在对非弹性散射γ计数和俘获γ计数以时间卡段进行区分后，再选择近热中子以及近超热中子计数对非弹性γ计数进行校正的效果更好。分析斯伦贝谢算法的计算结果可知，该算法对岩性校正的能力较弱，不能取得良好效果，同时计算精度也略低于本文算法。

4 结论

本文采用MCNP模拟软件，通过建立可控中子源新型一体化测井仪以及相关的地层模拟模型，研究了地层密度与探测器接收到的与地层发生相互作用后的γ计数、中子计数的响应关系，分析了不同岩性地层下的密度计算结果，最终建立了一种在岩性校正方面优于斯伦贝谢密度算法、在计算精度方面优于哈里伯顿密度算法的新型密度算法。综上所述，本文所建密度算法更适合于现有仪器，且由于不依赖探测器绝对计数具有更高的测量稳定性。

研究中发现，在本文密度算法和哈里伯顿密度算法中，计算误差会在某些特定孔隙度下明显变大，而斯伦贝谢算法的计算误差依旧对岩性较敏感，且在3种岩性条件下，计算误差均存在随密度的增大先减少后增大的变化趋势，这些问题目前还没有找到合理的解释，有待进一步研究。