束流漂移对硅条探测器阵列测量的影响

孙浩瀚，林承键,3,*，马南茹，王东玺，贾会明，杨 磊，杨 峰，钟福鹏,3，温培威，姚永进,4

(1.中国原子能科学研究院，北京 102413；2.国防科技工业抗辐照应用技术创新中心，北京 102413；3.广西师范大学，广西 桂林 541004；4.北京航空航天大学，北京 100083)

随着对重离子核反应机制研究的不断深入，需对多种出射产物进行运动学完全的符合测量。如在研究库仑势垒能区弱束缚核体系的6Li+209Bi破裂反应中，出射产物包括p、d、t、α、6Li等多种不同质量和不同角分布的带电粒子[1]。这不仅要求探测器阵列具备强的ΔE-E粒子鉴别能力，也要求探测器阵列覆盖较大的立体角，才能有较大的几何探测效率，以得到反应Q值谱、破裂产物的相对能量、动量和角关联谱等，从而重构破裂过程中靶核和破裂母核所处的激发态，得到各核态的破裂分支比等关键的物理信息。另一方面，在有效的测量时间和束流强度一定的情况下，实验探测到的各角度粒子数必须达到足够进行后续物理分析的统计量，这同样要求探测器阵列具有足够大的立体角和足够高的探测效率。近年来，随着半导体探测器技术的不断发展，多个平面硅工艺的难题得到了解决。氧化钝化、离子注入、光刻等技术的使用使得半导体探测器的性能大幅提高。借用这些新的设计和工艺研制出了大面积双面硅条探测器(DSSD)[2]。

DSSD是一种PIN型半导体探测器，其正、背面均由多条电极构成，电极相互垂直，可同时给出两个方向的位置信号，具有位置和能量分辨率高、线性范围宽、响应时间快、体积小等诸多优点[3]。将DSSD与单面四分硅探测器(QSD)组合成探测器望远镜，可测量ΔE-E从而鉴别带电粒子，进一步可将多组探测器望远镜组装成大立体角覆盖的硅条探测器阵列。国际上著名的阵列有MUST2[4]、HiRA[5]、TIARA[6]、DRAGON[7]、GLORIA[8]等。

硅条探测器阵列普遍具有结构紧凑、覆盖面积大、探测器与靶距离近等特点，因此整个阵列上的计数易受安装条件和束流情况等因素的影响。如放射性核束的束斑普遍较大(直径约10 mm左右)，反应点的不同会引起立体角很大的变化，因此通常在靶前放置位置灵敏探测器，如平行板雪崩计数器(PPAC)等，以重构入射束流的方向及束流在靶上的实际反应点；对串列加速器产生的束流而言，虽然束斑小(直径约1 mm)，但可能存在束流漂移而导致反应点的变化。本文拟在蒙特卡罗模拟的基础上，结合具体的串列实验，讨论束流漂移对探测器测量的影响，给出避免这种影响的措施，并给出修正后的弹性散射角分布作为示例。

1 实验设置

1.1 硅条探测器阵列

实验中所用的硅条探测器阵列由8组三重ΔE1-ΔE2-ER望远镜单元组成。每组望远镜单元的第1层为厚度40 μm(或60 μm)、正背面各16条(条宽为3.0 mm，条间距为0.1 mm)的DSSD，第2层为厚度300 μm的QSD，第3层为厚度1 000 μm(或1 500 μm)的QSD。每层探测器的有效面积均为50 mm×50 mm，能量分辨率好于1%[9]。这种三重望远镜能有效实现轻离子和重离子、低能和高能带电粒子的同时鉴别。

8组望远镜单元安装在由3D打印制成的支架上，几何误差可控制在0.1 mm左右，整体结构如图1所示。图1a中箭头为束流入射方向，靶位于阵列中心，编号1～8为8组望远镜单元，其中望远镜单元1、2、3、4放置在后角，望远镜单元5、6与束流方向垂直，望远镜单元7、8放置在前角。8组望远镜单元均正对靶，8组望远镜单元的中心均距靶心70 mm，相对束流具有严格的对称结构。图1b显示了以束流方向为z轴，束流水平方向为x轴，竖直方向为y轴建立的直角坐标系。

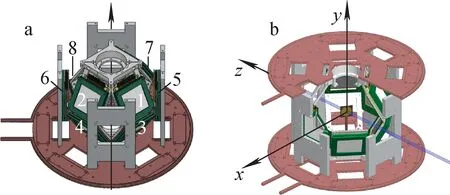
图1 硅条探测器阵列(a)和阵列上所建立的xyz坐标系(b)

每块DSSD包含3 mm×3 mm的256个方格，由它们的(x,y,z)坐标可计算出球坐标下的(r,θ,φ)。图2示出了每个方格4个顶点对应的(θ,φ)，这样每个方格所覆盖的立体角dΩ=sinθdθdφ。可看出望远镜单元1～4覆盖θ为107.6°～155.7°，望远镜单元5和6为74.2°～105.9°，望远镜单元7和8为24.3°～72.4°。

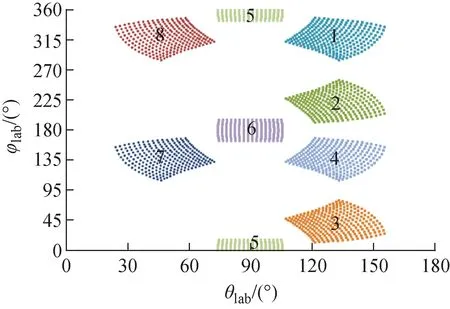
图2 探测器阵列所覆盖的角度

1.2 实验

实验在中国原子能科学研究院北京HI-13串列加速器核物理国家实验室R60管道终端的散射靶室上进行。束流为25 MeV和40 MeV的6Li，轰击质量厚度约100 μg/cm2的自支撑209Bi靶。靶内框近似为椭圆形，长边±6 mm，短边±4.5 mm。调束时在靶位放置1个直径3 mm的光阑，通过传输效率判断束流是否打在靶中心。通常串列束流的束斑直径约1 mm，要求传输效率达80%以上。实验的主要目的是关联测量6Li破裂的α和d，也做了单举测量以获得弹性散射的数据。

硅条探测器阵列安装在靶室中心，由靶室底座与阵列中心支架的密接触保证几何安装的正确性，并用激光水平仪校验。靶室前角安装4个金硅面垒探测器作为束流监测器，金硅面垒探测器均距离靶250 mm，与束流的夹角分别为上下25°和左右12.5°，可保证探测到的基本为卢瑟福弹性散射事件。其中上、下监测器的光阑直径为1.0 mm，左、右监测器的光阑直径为0.5 mm。

2 束流漂移的蒙特卡罗模拟

束流漂移对出射粒子角分布的影响主要有两个方面——立体角的变化和散射角的变化。对于停阻在靶上的熔合蒸发残余核的α衰变，可当作α源进行刻度，其角分布是各向同性的，故束流漂移的影响全部体现在立体角的变化上；而弹性散射截面受散射角的影响很大，因此除立体角变化外，束流漂移的影响也体现在由散射角变化导致的截面变化上。

蒙特卡罗方法是一种随机抽样的数学计算方法，基本思想是频率替代概率，均值替代数学期望[10]。本文利用蒙特卡罗模拟探测器本征几何效率及束流漂移在两种情形下对出射粒子角分布的影响，每次模拟的事件数均为106。

2.1 本征几何效率

首先确定理想状况下探测器阵列的几何探测效率，即中心点源对应的探测器阵列的立体角分布。假定发射源为点源，其发射的粒子数和探测器收集的粒子数以及两者的比值如图3所示。根据两者的比值可得到探测器阵列的本征几何效率为26.8%，即覆盖26.8%的4π立体角。

2.2 束流漂移对熔合蒸发残余核α衰变测量的影响

实验束斑直径约1 mm，模拟时假定熔合蒸发残余核在直径1 mm的圆内均匀分布。若靶平面与束流垂直，则z方向无漂移；若靶平面倾斜，即靶平面的法线与束流方向形成夹角β，则束流在z方向也会发生漂移，漂移距离为Δxtanβ(Δx为x方向漂移距离)。

分别考虑束流x、y、z3个方向上的漂移对角分布造成的影响。假设漂移距离为6.0 mm时，实验室系8个DSSD上计数的角度分布以及它们分别与无漂移时计数的比值如图4所示。可看出，3条曲线之间的计数变化不超过3%，彼此几乎重合。比值的涨落很大程度上是统计误差造成的。这表明即使束流漂移至最大距离，由于α衰变各向同性的特性，在3%的误差范围内，探测器阵列上的衰变计数受束流漂移的影响亦可忽略。

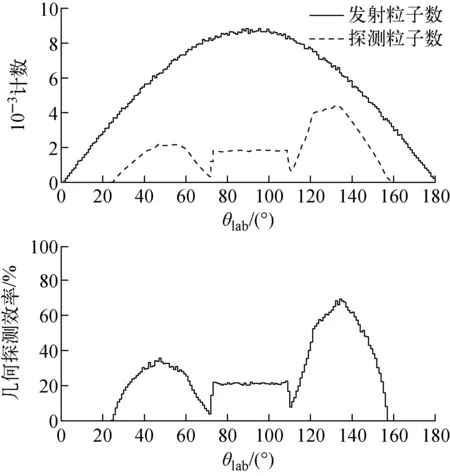
图3 计数和探测效率随角度的变化

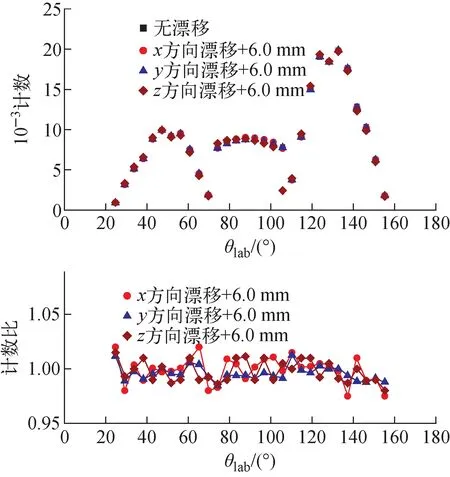
图4 x、y、z方向的束流漂移对测量的α衰变角分布的影响

2.3 束流漂移对卢瑟福散射测量的影响

模拟时入射粒子6Li的实验室系能量为40 MeV，靶为209Bi。球坐标系下，φ在[0,2π]均匀分布，θlab的抽样满足卢瑟福散射公式：

σRu(θlab)=1.296(Z1Z2/Elab)2·

[csc4(θlab/2)-2(A1/A2)2]

(1)

式中：σRu为卢瑟福散射截面；Z1、Z2为弹核和靶核的核电荷数；A1、A2为弹核和靶核的质量数；Elab为弹核实验室系能量。

计数与截面之间的关系满足：

σRu(θ)=dN/INSdΩ

(2)

式中：I为束流强度；NS为靶单位面积的核子数；dΩ为单位立体角。模拟束斑直径为1 mm，圆内均匀抽样。束流在x、y、z方向漂移±1.5、±3.0、±4.5、±6.0 mm时，望远镜单元7 DSSD上计数的角分布以及它们分别与无漂移时计数的比值如图5所示。图中x、y、z方向上束流漂移引起的计数变化均随散射角的增加而逐渐减小。这是由于卢瑟福散射截面在前角区对散射角最敏感，至90°和后角区时，对角度的变化已不再敏感。因此更后角处望远镜单元1～6 DSSD的计数变化相对很小，不再细述。由于望远镜单元7和8 DSSD的对称性，它们的角分布是相同的。

由于图5中的角分布实际为计数在θ方向上的投影分布，因此直角坐标系(x,y,z)转换为球坐标系(r,θ,φ)后，束流在x、y、z方向上的漂移对θ所产生的影响并不相同，因此角分布受到的影响也不相同。其中，x方向漂移引起的影响最大，z方向次之，y方向的影响最小。将最明显的x方向漂移对望远镜单元7 DSSD有漂移与无漂移时计数比的影响列于表1。可看到，束流漂移将给单个DSSD，尤其是位于前角的DSSD上的计数角分布造成很大影响。

实际上，抽取角分布用到的是望远镜单元7和8 DSSD计数之和。若束流向右侧漂移导致望远镜单元7 DSSD上的计数增加，位于对称位置的望远镜单元8 DSSD上的计数将会减少，因此会起到一定的互补作用，其有漂移与无漂移时计数比平均值的偏差将极大减小。作为对比，表1也列出了望远镜单元7和8有漂移与无漂移时计数比的平均值随漂移距离的变化。可看出，望远镜单元的对称放置极大减弱了束流漂移带来的影响。当漂移距离小于3.0 mm时，由于对称性的抵消作用，整个阵列计数受到的影响在10%以下；漂移距离小于1.5 mm时，阵列计数受到的影响不超过5%。

图5 x、y、z方向束流漂移对测量的卢瑟福散射角分布的影响

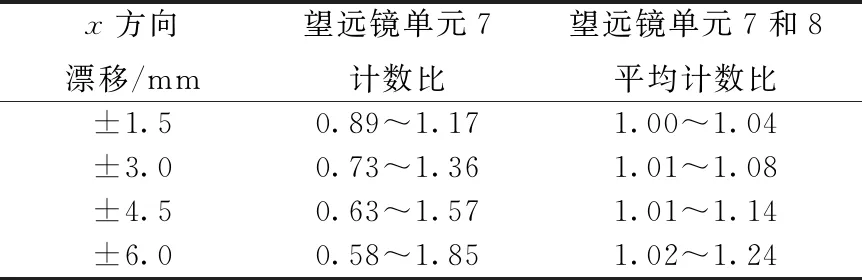
表1 束流x方向漂移对望远镜单元7计数比以及对望远镜单元7和8平均计数比的影响

3 实验数据分析

通过安装在前角的4个束流监测器收集的卢瑟福散射事件计数得到束流在整个实验过程中的实际漂移距离。结合阵列计数在不同漂移距离下受到的影响的蒙特卡罗模拟结果，就可得到实验中束流漂移对硅条探测器阵列测量的影响。

3.1 束流漂移监测

将左、右监测器M1、M2的计数记为N1、N2；上、下监测器M4、M3的计数记为N4、N3。理想情况下N2/N1和N4/N3均等于1。束流沿x正方向漂移前后的变化如图6所示，z和z′为漂移前后的束流方向。根据OO′距离l21即可计算出漂移后M1、M2对应的角度θ1、θ2和立体角dΩ1、dΩ2。根据式(1)、(2)可得到漂移后M2、M1的理论计数比值K21。

K21=f(l21)=dN2/dN1=

(3)

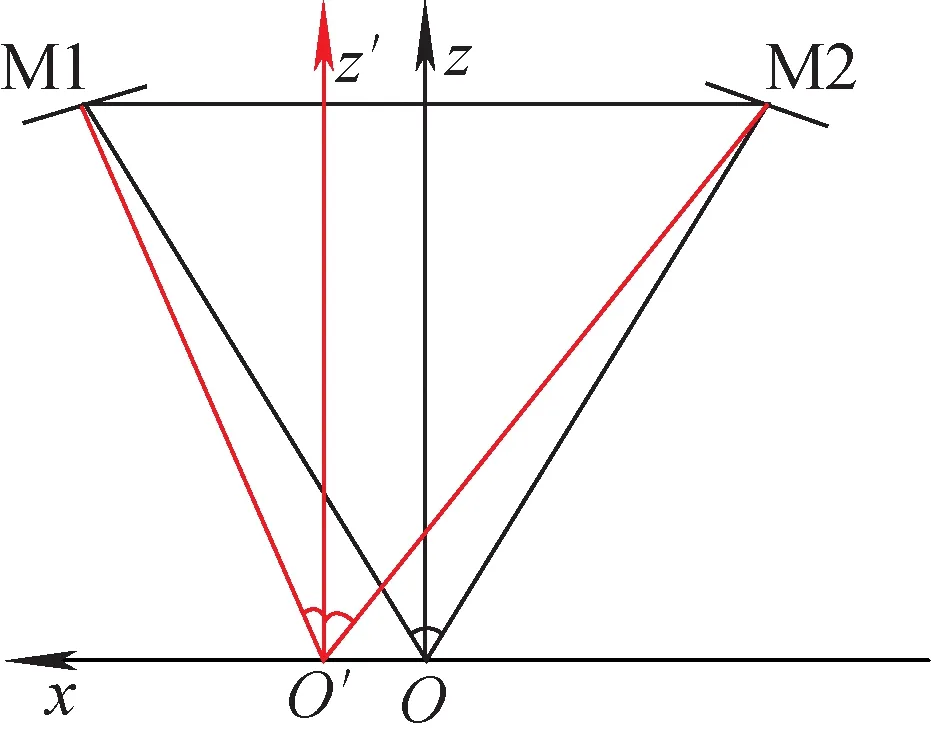
图6 束流漂移示意图

由于金硅面垒探测器前的光阑很小(直径不超过1 mm)，但和靶的距离达250 mm，因此立体角的变化很不明显，而卢瑟福散射截面的变化相对很大，dΩ2/dΩ1可忽略。

求解式(3)的反函数后就可根据K21(或K43)的值求出l21(或l43)，但该函数的解析表达式较复杂，采用数值方法求解较简单。即在-4.5～4.5 mm之间每隔0.225 mm取点，得到l21-K21、l43-K43的系列散点，如图7所示，考虑到其与对数函数图像的相似性，用对数函数进行拟合，得到两条拟合曲线为：

l21=7.000 4lnK21

(4)

l43=7.000 4lnK43

(5)

两条曲线的相关系数R2均达1.000 00，能满足高精度下的插值求解，但z方向的漂移对K21和K43无影响。

实验共计239轮数据，用式(4)和(5)计算每轮对应的左右偏移l21和上下偏移l43，得到束流漂移的二维分布，零点为统计加权的分布中心，如图8所示。图中实线为靶框范围，点划线为调束光阑范围。可看出，全部轮次的漂移均在半径3.0 mm圆内，其中86%轮次(计数占比为89%)的漂移在调束光阑限制的半径1.5 mm圆内。这说明在实验过程中，束流保持了较好的稳定性。另外，用于抽取25 MeV和40 MeV弹性散射角分布的单举测量结果亦示于图8。可看到，两个能点的统计加权的中心并不在一起。

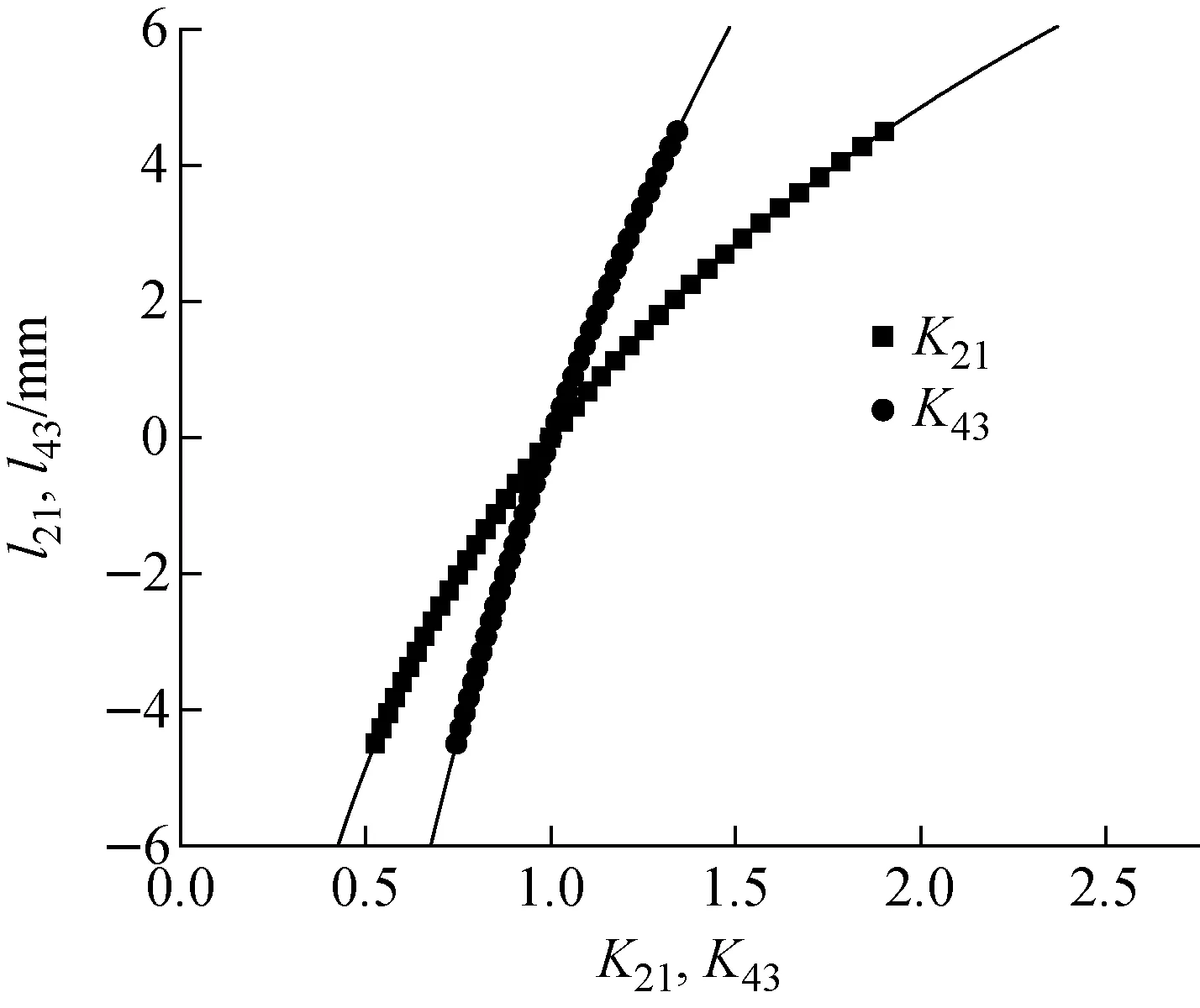
图7 监视器计数比值对应的漂移量

3.2 弹性散射角分布抽取

首先利用蒙特卡罗模拟方法，对图8中每轮25 MeV和40 MeV单举轮次实验数据所对应的实际束流漂移距离进行修正，然后利用模拟刻度、衰变刻度和束流刻度3种刻度立体角的方法，得到弹性散射截面与卢瑟福散射截面的比值[11]。模拟刻度使用蒙特卡罗模拟刻度立体角，即未考虑几何误差的理论情况；衰变刻度是利用实验中熔合蒸发残余核的α衰变刻度立体角，包含了束流信息和阵列安装的位置信息等；束流刻度是将能量低于库仑势垒(势垒高度约30 MeV)时的弹性散射截面作为标准卢瑟福散射截面进行立体角刻度，同样考虑了实验中的系统误差。

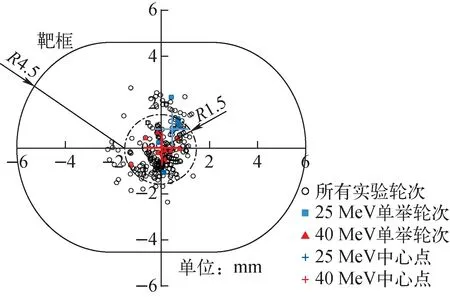
图8 实验测得的束流漂移分布(沿束流入射方向)

用模拟刻度和衰变刻度方法得到的25 MeV和40 MeV6Li+209Bi角分布如图9a所示。图中明显掉下的点是DSSD的边缘引起的。作为对比，图9a也示出了修正束流漂移前、后模拟刻度得到的角分布变化。可看出，束流漂移只对最前角区域的部分数据点产生了影响，根据前面的分析，由于阵列对称性的优势，漂移影响在5%以下。模拟刻度误差为弹性峰计数的统计误差，未考虑系统误差。衰变刻度误差为弹性峰计数与衰变峰计数的比值的统计误差，几何引起的误差相互抵消。两者比较，衰变刻度误差更小，计数掉落更不明显，结果更精确。v

图9 模拟刻度和衰变刻度得到的25 MeV和40 MeV 6Li+209Bi的弹性散射角分布(a)和束流刻度得到的40 MeV 6Li+209Bi的弹性散射角分布(b)

用束流刻度方法，以25 MeV截面作为卢瑟福散射截面，得到的40 MeV角分布结果如图9b所示，误差为40 MeV弹性峰计数与25 MeV弹性峰计数比值的统计误差，几何引起的误差相互抵消。根据图9b，束流刻度时误差最小，计数掉落的现象基本消失。

图9b示出了文献[12]中40 MeV6Li+209Bi的实验结果，以及用Ptolemy程序[13]进行光学模型拟合的结果，与文献数据基本一致。该能量下的弹性散射规律符合能量高于库仑势垒时产生的菲涅耳(Fresnel)散射规律[11]，后角区由于核吸收效应，截面快速下降。

4 小结

本文讨论了束流漂移对大型硅条探测器阵列计数测量的影响。根据蒙特卡罗模拟得到在α衰变和卢瑟福散射两种情形中，束流在不同方向漂移不同的距离后对计数角分布造成的不同影响，并讨论了阵列对称性布置的优势是能消除束流漂移带来的大部分误差；其次，根据束流监测器计数，得出在大多数时间内实验束流的漂移距离小于1.5 mm的结论，表明了实验过程中北京HI-13串列加速器束流具备较高的稳定性。无论是α衰变还是对散射角最敏感的卢瑟福散射，由于对称性的抵消作用，在漂移距离小于1.5 mm(3.0 mm)时，对阵列测量造成的影响在5%(10%)的误差范围内。在修正束流漂移后，利用3种刻度立体角的方法——模拟刻度、衰变刻度和束流刻度，得到25 MeV和40 MeV6Li+209Bi弹性散射的角分布，其中40 MeV的角分布与文献结果基本一致。