ANU，ANU-II和LiCi算法的积分区分器搜索

王红艳，韦永壮，刘文芬

1(桂林电子科技大学 广西密码学与信息安全重点实验室，广西 桂林 541004) 2(桂林电子科技大学 广西高校云计算与复杂系统重点实验室，广西 桂林 541004) 3(桂林电子科技大学 广西无线宽带通信与信号处理重点实验室，广西 桂林 541004)

1 引 言

随着物联网IOT(Internet of Things)技术的飞速发展，嵌入式系统、无线通信和智能卡等已普及到人们生活的方方面面.由于轻量级分组密码算法具有低功耗、结构轻便和占用面积小等特点，所以较适用于资源受限的环境中.ANU[1]，ANU-II[2]和LiCi算法[3]是新提出的基于比特来设计的三个超轻量级密码算法.它们的设计理念都是通过尽可能低的轮数来获取最大数目的活跃S盒个数.并且ANU-II是Dahiphale等人在ANU基础上改进的轻量级密码算法，该算法舍去ANU算法的P置换后，相应在算法结构上进行新的变换，使得算法在实现效率和安全性方面都有进一步提升.目前，对于三个算法的最新攻击进展如下：2016年印度学者Bansod等人针对ANU算法分别给出8轮的零相关线性区分器和4轮的不可能差分区分器[1]；2017年Patil等人给出LiCi算法6轮的零相关线性区分器[3]；2019年Xin等人给出LiCi算法的12轮积分区分器，活跃比特为263个选择明文1,[11]；2019年Wei等人利用S盒的特殊性质，给出LiCi算法10轮的不可能差分区分器[10].

近年来，自动搜索技术对密码算法的安全性分析起到很大的推进作用.与传统手动运算相比，其具有操作简易、精确性高和效率高等优点.积分攻击[4]是2002年Knudsen等人在Square攻击基础上提出一种选择明文的密码分析方法.通常使用积分性质的传播特性和评估代数次数两种方法来构造区分器.在EUROCRYPT2015上Todo等人提出了可分性质[5]，它是在积分攻击基础上进行推广的一种新分析方法.利用可分性质，介于“BALANCE”和“ALL”之间的隐含关系可以更明确的表达出来.相比传统积分攻击，可分性对密码算法要求局限性更小，更适用于非双射、低代数次数、比特级等分组密码算法中.2015年Todo等人利用可分性质以及S盒的特殊性质成功分析了全轮的MISTY1算法[6]；2016年Xiang等人利用基于比特可分性和MILP相结合的思想，实现了对6个密码算法的区分器搜索[7]；2019年Hu等人利用三子集可分性质提出一个自动搜索模型-STP，该模型具有不限制算法分组大小的优点[8]；2019年Hao Y和Todo等人提出超级多项式的代数性质应用到基于比特可分性的立方攻击中[9].由于传统比特级可分性限制了对分组较长算法的应用，Xiang等人提出利用线性不等式来刻画比特可分性的传播特性，并构建相关MILP模型.注意到，对于ANU，ANU-II和LiCi算法是否能抵御比特可分性质的积分分析这一问题仍有待解决.

此外，在密码算法攻击中，区分器轮数的高低更能准确的衡量密码算法的安全性.本文首次对ANU和ANU-II算法进行比特积分分析，构建其新的可分性MILP模型，给出了针对ANU和ANU-II算法9轮和8轮的积分区分器自动搜索方法.并利用LiCi算法变形的等价结构，构建新的MILP模型，给出了12轮积分区分器.对于以上三个算法，这是目前最优的区分器攻击结果.

2 算法介绍

2.1 符号说明

P，C：64比特明文和密文

K：80比特主密钥

RKi：第i轮的32比特轮密钥

Li，Ri：第i轮左分支(右分支)32比特输入

⊕：按位异或操作(XOR)

<<<α：左循环左移α比特

>>>β：右循环右移β比特

‖：二进制连接符

2.2 ANU和ANU-II算法简介

2.2.1 ANU算法

ANU算法[1]是2016年印度学者Bansod等人提出的一种基于Feistel结构的超轻量级分组密码算法.该算法采用基于比特的置换形式，分组长度为64比特，密钥长度支持80和128比特两个版本，迭代轮数为25轮.ANU算法结构如图1所示.

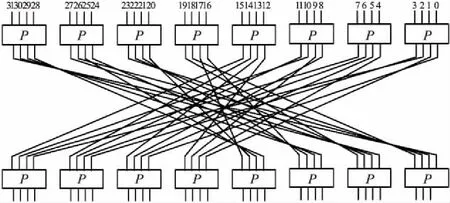
图2 ANU算法的P置换

ANU算法的轮函数F由密钥加、异或运算、字节替换和循环移位等四种基本运算构成.设PT为输入，CT为输出，则ANU算法加密流程如下：

PT=Li‖Ri，0≤i<25

Ri+1=P(Li)，Li+1=S(Li<<<3)⊕Ri，

Li+1=P[(S(Li>>>8)⊕Li+1)⊕RKi].

CT=Li+1‖Ri+1

2.2.2 ANU-II算法

ANU-II算法[2]是Dahiphale等人在BID2017上提出的一种轻量级分组密码算法.该算法是在ANU基础上进行优化，并舍去P置换线性操作.其分组长度为64比特，密钥长度为128比特，共迭代25轮.ANU-II算法结构如图3所示.

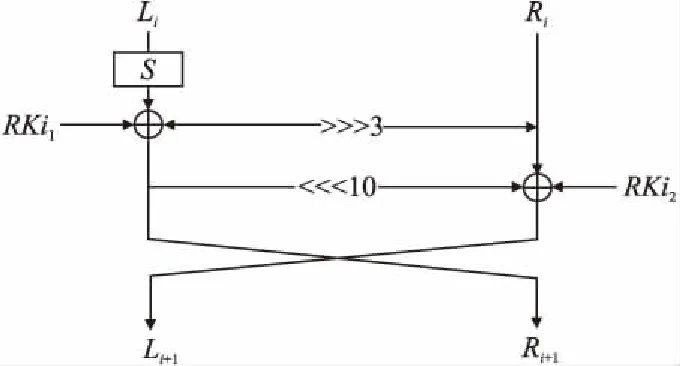
图3 ANU-II算法结构

关于ANU-II的加密流程：

PT=Li‖Ri，0≤i<25

Ri+1=[S(Li)]⊕(Ri>>>3)⊕RKi1，

Li+1=[(Ri+1)<<<10]⊕Ri⊕RKi2.

CT=Li+1‖Ri+1

由于对ANU和ANU-II算法的比特积分攻击不需要考虑密钥编排算法，所以这里不再作详细介绍，具体可参见文献[1,2].

2.3 LiCi算法简介

LiCi算法[3]是Patil等人在ICET2017上提出的一种超轻量级分组密码算法.该算法分组长度为64比特，密钥长度为128比特，共迭代31轮.LiCi算法的结构(等价结构)如图4、图5)所示.

如图5是LiCi算法的等价结构，可看作该算法的一轮加密运算由两个简单的Feistel结构相接而成.关于LiCi算法的加密流程如下：

PT=Li‖Ri，0≤i<31

Li+1=(S(Li)⊕RKi1⊕Ri)<<<3，

Ri+1=(S(Li)⊕RKi2⊕Li+1)>>>7.

CT=Li+1‖Ri+1

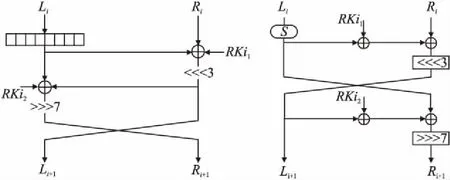
图4 LiCi算法结构

Fig.4 Structure of LiCi

图5 LiCi算法的等价结构

Fig.5 Equivalent structure of LiCi

由于对LiCi算法的比特积分攻击同样不考虑密钥编排，具体可参见文献[3].

3 可分性分析

3.1 可分性和可分性路径

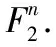
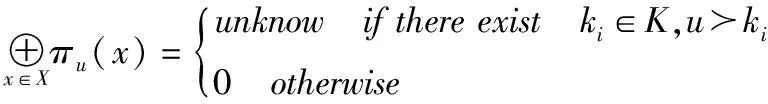
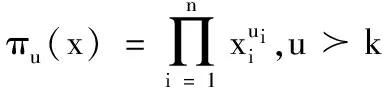
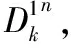
其中(k0，k1，…，kr)∈K0×K1×…Kr，对于所有i∈{1，2，…，r}都有ki-1传播到ki，那么记r轮可分性路径为(k0，k1，…，kr).最后集合Kr之间的关系用来判断是否存在有效积分区分器.

3.2 可分性的传播规则

2015年Todo等人给出了传统可分性质的传播规则[5].但基于比特可分性质，这里只用到Copy和XOR两种基本操作，具体的传播规则这里不再多加赘述，详细可参考文献[5,6,12].下面用线性不等式组对COPY、XOR和AND操作的可分性传播进行模型化，如下所示：

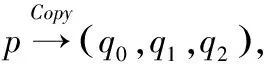
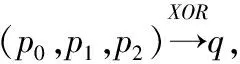
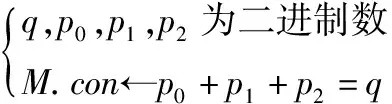
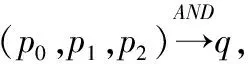
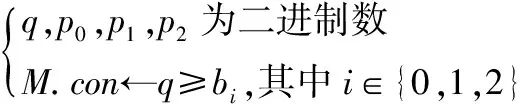
3.3 混合整数线性规划(MILP)

MILP问题是一种优化求解问题，即在约束条件下取目标函数的最优解(即最大最小值问题).构建一个MILP模型M，需要包括变量a，b，c，限制条件M.con和目标函数M.obj，并且其中的变量仅限于整数.下面举例1来说明：

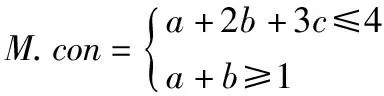
然而，MILP求解器仅用来评估该模型是否具有可行性，也就是说如果没有目标函数和可行解决方案，则此模型不可行.所以本实验根据搜索算法的具体特征，使用Gurobi优化器来求解该模型.

3.4 SAGE中的不等式生成函数

通过Sage软件中的Inequality_generator()函数，把经过S盒的可分性路径用一系列不等式来表示，核心代码如下：

Points=[[0，0，0，0]，[0，0，1，0]，…]

Triangle=Polyhedron(vertices = Points)

for l in triangle.inequality_generator()：

print l

4 可分性MILP模型的构建

ANU，ANU-II和LiCi算法总体都采用广义Feistel结构.我们利用文献[7]的思想，针对以上三个算法结构的本身特性，给出了构建基于比特可分性的新MILP模型来搜索积分区分器的自动化搜索方法，可分为以下3个步骤：

1)给出初始比特可分性，即给定具体的活跃bit和常量值.然后将密码算法轮函数分解为Copy、AND和XOR等基本运算.

2)利用1中基本运算的可分性质，根据三个算法本身的结构特性来构建经过轮函数的可分性路径的MILP模型，包括非线性层和置换层.

3)选择合适的目标函数，即搜索终止条件.重复r次可得到r轮轮函数的可分性MILP模型M.

由于密码算法中密钥加、轮常数异或等运算不影响可分性质，所以这里不作考虑.

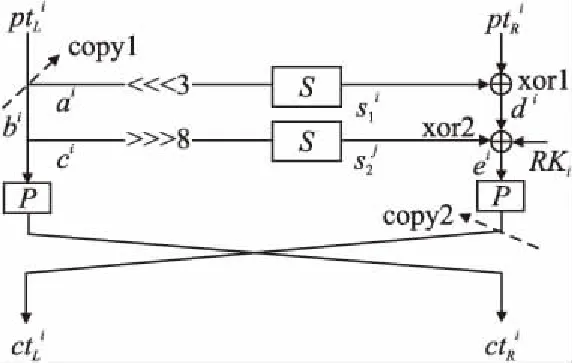
图6 ANU的MILP模型变量之间的关系

下面以ANU算法为例，针对密码算法的轮函数分解为XOR和COPY等基本运算，构建其MILP模型.同理ANU-II和LiCi算法与之思想类似，就不再详细介绍.如图6所示.

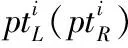
算法1.对ANU算法XOR函数的MILP模型

forn= 0；n<25 ;n++ do

end for

算法2.对ANU算法COPY函数的MILP模型

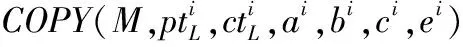
forn=0；n<25；n++ do

end for

4.1 ANU算法的MILP模型

4.1.1 模型化S盒

ANU算法由两个相同4*4的S盒构成，计算可得到经过S盒的输入输出可分性的48条可分性路径{D，C}，具体如表1所示.

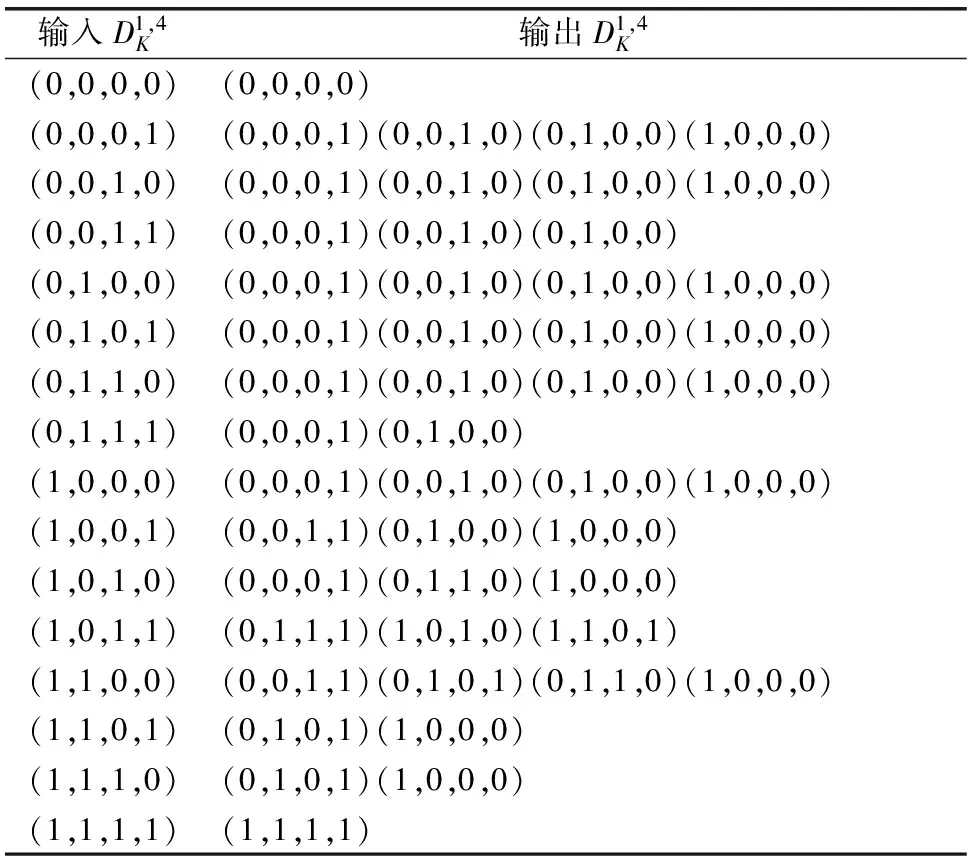
表1 ANU算法S盒的可分性路径

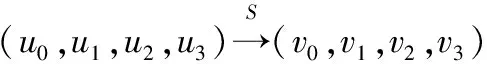
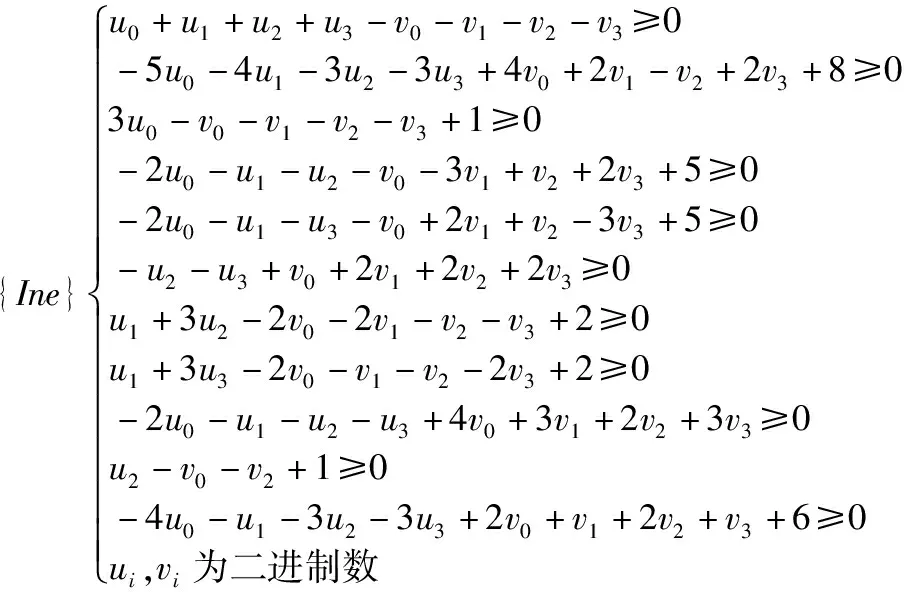
4.1.2 模型化置换层

对于一些置换层较为复杂的算法，可通过引入一些中间变量来描述置换层分解为COPY和XOR后的操作，从而来构建相关MILP模型.ANU算法的置换层由基于比特的P置换构成，运用简单拉线变换，即得到一条经过置换层的输入输出可分性的可分性路径.

4.2 ANU-II算法的MILP模型

ANU-II算法不含有置换层，所以仅对S盒来构建相关比特可分性的新MILP模型.经过计算可得到经过S盒的输入输出可分性的48条可分性路径{D，C}，具体如表2所示.

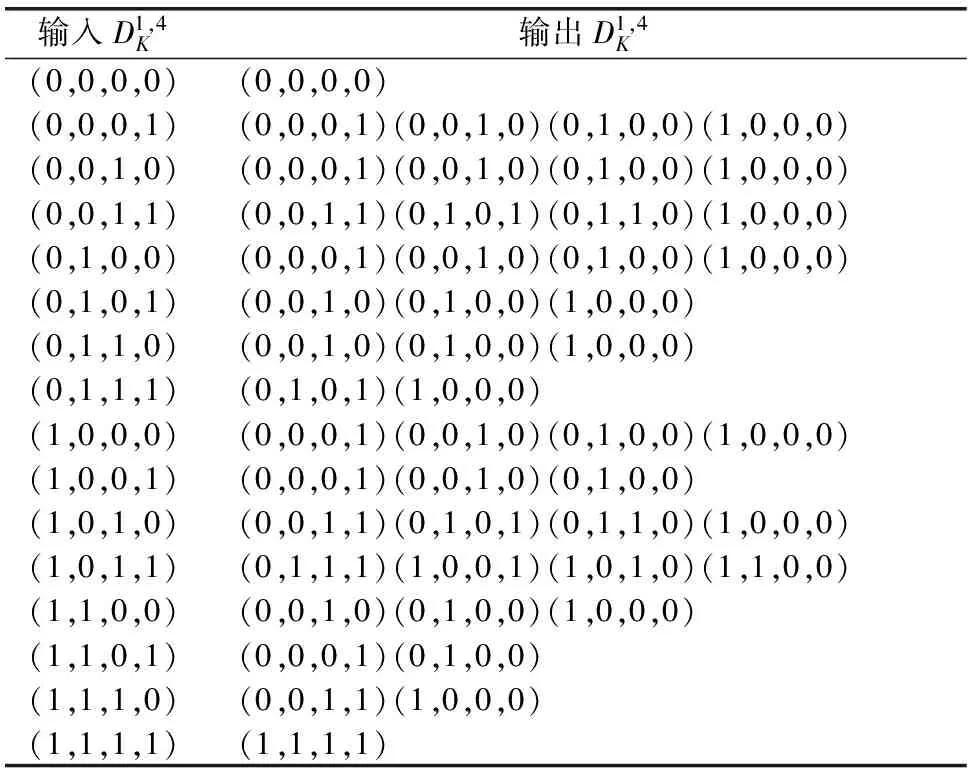
表2 ANU-II算法S盒的可分性路径

其次，通过Sage软件中的不等式生成函数(参考3.4节)，利用贪婪算法对生成198个线性不等式进行约减到11个，则约减不等式{Ine}如下.

4.3 LiCi算法的MILP模型

由于LiCi算法不含有置换层，所以仅对其4×4的S盒，来构建比特可分性的新MILP模型.计算可得到经过S盒输入输出可分性的48条可分路径{D，C}，具体如表3所示.

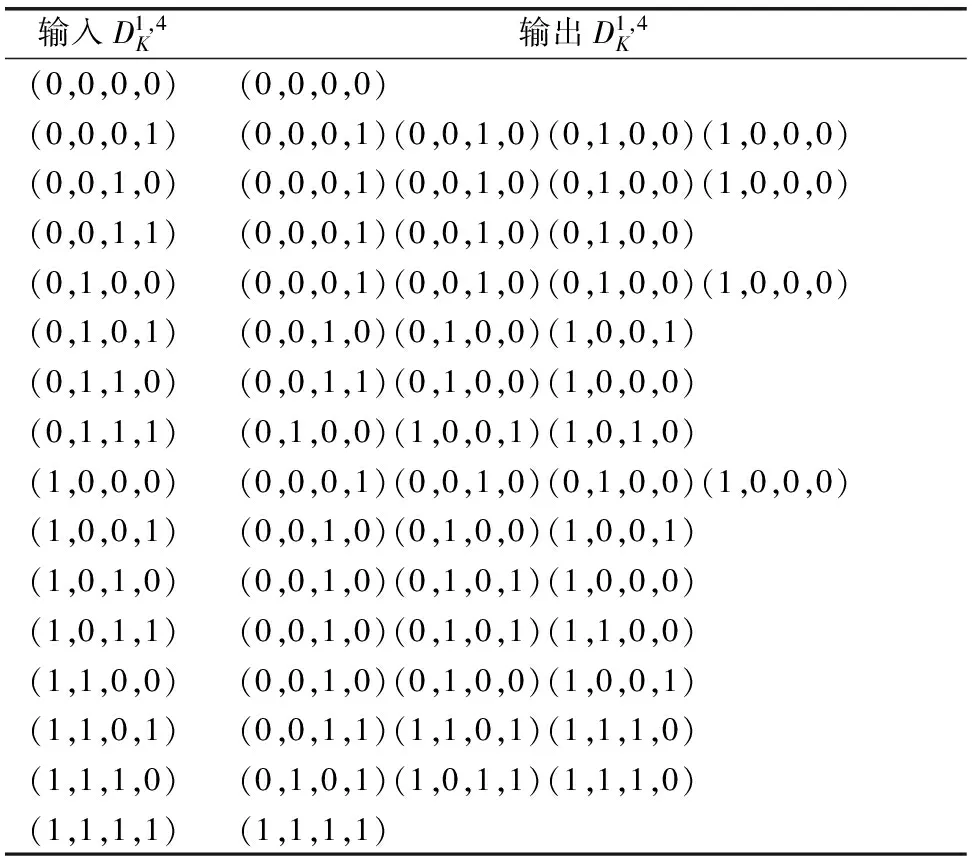
表3 LiCi算法S盒的可分性路径

其次，通过Sage软件中的不等式生成函数(参考3.4节)，利用贪婪算法的思想对生成187个线性不等式进行约减到15个，则约减不等式{Ine}表示如下：

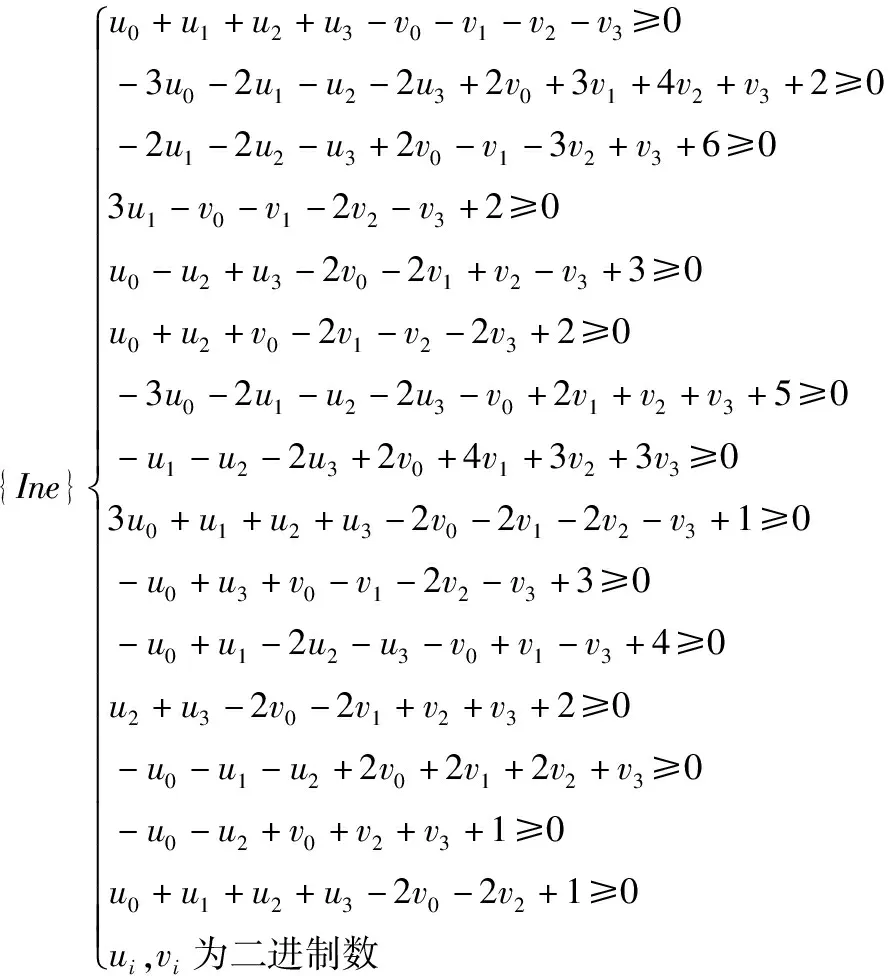
4.4 目标函数

由定义2可知，搜索是否存在r轮的积分区分器，只需检测是否存在零和性质.即判断Kr是否包含所有的单位向量e，步骤如下所示：

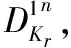
5 实验分析结果

本文采用的实验研究平台：采用Intel(R)Core(TM)i5-3230M CPU @ 2.60Hz，RAM-4GB，x64 Windows 10.首先根据第3节可分性性质相关定义，其次结合ANU，ANU-II和LiCi三个密码算法的本身结构特性，构建新的MILP模型(算法1、算法2).最后选择合适的目标函数、终止条件和限制条件，利用Gurobi优化器来求解该模型，搜索是否存在可用的积分区分器.设Ci为i个常量比特，Ai为i个活跃比特，Bi为i个平衡比特和Ui为i个未知比特，输入比特→输出比特.对以上三个算法搜索的区分器结果如下：

1)ANU算法的积分区分器：

2)ANU-II算法的积分区分器：

3)LiCi算法的积分区分器：

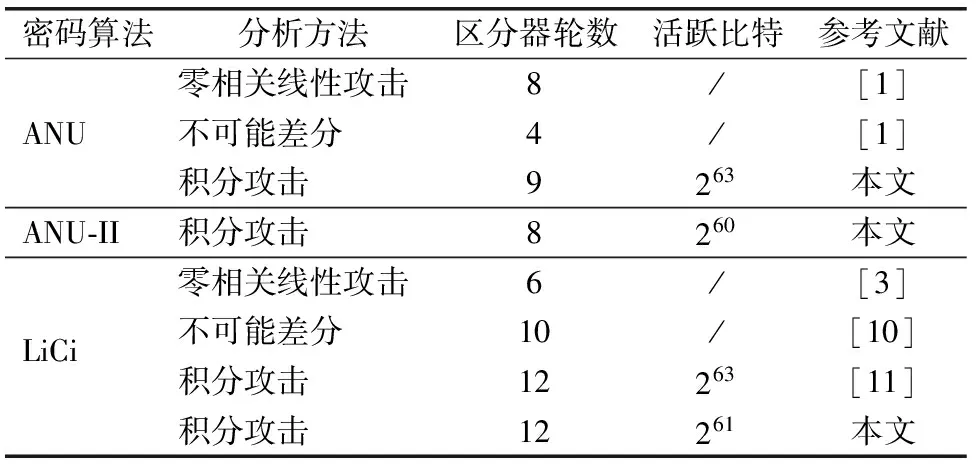
表4 ANU，ANU-II和LiCi攻击结果对比

上述结果表明，本文对以上三个算法所得到的区分器优于目前其他分析方法，如差分线性、不可能差分、零相关线性等.对比结果如表4所示.

6 结束语

目前对ANU，ANU-II和LiCi算法的分析有：差分/线性、零相关分析以及不可能差分等分析方法.注意到，对于以上三个算法是否能抵御基于比特积分攻击的这一问题仍有待解决.此外，在密码算法攻击中，所攻击的区分器轮数高低优劣更能准确的衡量密码算法的安全性，也更具有参考价值.

本文针对ANU，ANU-II和LiCi算法的结构特性，构建新的比特可分性MILP模型，给出了三个算法的9轮、8轮和12轮的积分区分器自动化搜索方法.相比其他已知的分析方法，本文所得到三个算法的区分器轮数和选择明文量都是最优的，利用这些区分器可以得到更高轮的积分攻击.同时针对LiCi算法的结构进行变形，提出一种新的LiCi算法的等价结构.由于目前比特积分攻击没有考虑到密钥编排算法.我们可考虑对以上三个算法利用密钥间的特殊性质与可分性质相结合的思想，如立方攻击等方法来进一步提高密码算法的分析轮数.