天牛须搜索与遗传的混合算法

赵玉强，钱 谦，周田江，伏云发

1(昆明理工大学 信息工程与自动化学院，昆明 650500) 2(云南省计算机技术应用重点实验室，昆明 650500)

1 引 言

近年来，众多模拟自然界生物行为和物理变化特性的智能优化算法[1]被相继提出，这些算法的问题依赖度低且易于实现，一经提出便受到广泛关注.天牛须搜索算法(Beetle Antennae Search Algorithm,BAS)[2]是2017年提出的模仿甲虫类(以天牛为例)生物觅食过程的智能优化算法，该算法基于单个体搜索，结构简单，在求解单峰值问题时有较好的收敛速度和求解精度，在许多领域中得到广泛应用[3-5].但是，BAS算法是单个个体搜索，并非群体寻优，所以该算法缺乏一定的多样性，在后期寻优中容易陷入局部最优值，不利于复杂问题的求解，因此，许多学者对其进行了改进，文献[6]将单个体搜索变成群体搜索来提高寻优能力，将BAS算法与花朵授粉算法结合提出了BASFPA算法，文献[7]将BAS算法与神经网络结合用于预测风暴潮灾害并取得了一定成果.遗传算法(Genetic Algorithm,GA)[8]是一类理论较为完备的仿生优化算法，大部分的研究围绕在如何平衡对现有解的挖掘和对未知解的探索上，因为这很大程度上决定着种群的多样性，进而对算法的寻优能力和寻优速度产生重要的影响，现有文献对GA的改进主要体现在对选择、交叉和变异算子的改进上[9-11]，但这些改进往往依赖给定的某些参数或执行顺序，这使算法对某些临界参数比较敏感且不容易控制，反而有可能让算法陷入混乱的状态，为此，许多学者将遗传算法与其他算法结合提出了许多混合算法[12-15]，以此来弥补遗传算法自身的缺陷，相关研究在一定程度上取得了较好的结果.

在对BAS和GA的不足之处和各自优势的互补性进行分析的基础上，本文提出了一种基于BAS与GA的混合优化算法(Hybrid Optimization Algorithm Based on BAS and GA，BASGA).该算法先分别对两种算法进行了有针对性的改进，以最大限度发挥算法各自的优势，然后再将两者互补结合，产生新算法.具体来说，首先对BAS算法进行改进，提出基于多向探路模型的变步长反馈策略用以更新天牛个体的位置，并将改进的BAS嵌入到GA中来提升算法整体的收敛速度和精度.之后，为了提高种群的多样性，设计了一种扩展的多子代竞争交叉方式提高GA的探索能力，同时采用自适应方法调节交叉和变异概率以控制种群的多样性.最后，以函数优化问题为例与其他学者提出的混合算法进行了对比，实验结果证明BASGA算法在单峰值和多峰值函数优化求解中都具有较好的寻优性能.

2 基本算法的原理

2.1 GA算法的基本原理

遗传算法有不同的编码形式，本文采用实数编码的遗传算法.GA算法主要通过选择、交叉和变异操作来求解问题解.其中，选择操作是挖掘已有个体信息的主要手段，大多采用赌轮或随机抽样等比例方式来选择一定数量的优质个体并放入下一代种群中，以确保种群的进化方向.交叉和变异算子的作用是探索新的解：

1)交叉操作

实数GA大多采用算术交叉的方式进行染色体的杂交，以实现基因重组的目的.对任意两个染色体X和Y，其产生的子代X′,Y′可用式(1)表示：

X′=X+r1(Y-X)

Y′=X+r2(Y-X)

(1)

其中，r1和r2均是D个由(0,1)内均匀分布的随机数组成的向量，D是问题维度.

2)变异操作

在实数GA中，有多种方式实现对染色体的变异操作，大多数变异的基本原理是在原染色体上施加一个步长扰动来改变染色体的基因以达到变异的目的，如式(2)所示.

X′=X+ε

(2)

其中，X′是变异后的染色体，X是原染色体，ε是步长扰动因子.

常用的变异策略有均匀变异、非均匀变异、高斯变异、柯西变异等.

2.2 BAS算法的基本原理

BAS算法通过天牛个体在可行域中不断更新位置来找到全局最佳解.假设个体在D维解空间中的位置为X=(X1,X2,…,XD)，则其左右两只触须的位置Xr和Xl可以被定义为式(3)所示的模型：

(3)

个体在解空间不断对左右触须附近位置的适应度进行计算并向适应度高的位置方向进行移动.当前位置个体Xt根据式(4)的规则移动到下一个位置：

(4)

3 天牛须与遗传混合算法

BAS算法侧重过程搜索，有利于单峰问题的求解，GA算法是种群进化寻优，有利于多峰值问题的优化.根据BAS算法和GA算法各自的优势，本小节提出两者混合的算法.在混合之前，首先对两种算法的优点做进一步的强化，BAS算法进一步提高单个体寻优的速度和局部搜索能力，而GA算法则增强种群多样性以充分发挥其在全局寻优中的优势.

3.1 基于多向感知探路反馈的BAS算法

3.1.1 多向感知模型的构建

传统BAS算法中天牛触须提供了一种非左即右的探索方向，如图1(a)所示，个体只在当前位置两侧的触须方向计算适应度大小并进行比较，但因为触须朝向的随机性，导致个体有很大可能会错过当前位置附近更好的解，进而影响算法的搜索性能.实际上，甲虫触须在自然界中能够呈全角度转动的状态，并未被局限于两个相对方向，受此启发，本文建立多向感知模型，通过式(5)在个体当前位置产生n个单位向量作为右触须转动的探知方向，而左触须的探知方向取该向量的负值：

图1 天牛触须方向感知模型

(5)

其中，D表示求解问题的维度，rand是随机数产生函数.如图1(b)所示，与传统BAS只有两个探索方向不同，新的多向模型包含了n对探索方向，增大了个体对当前周围位置的探索范围，而且，算法可通过调节n的大小来调控探索的范围，因此多向模型能进一步提高算法的寻优能力和收敛速度.

在多向感知模型的基础上，通过式(6)可得到每对左右触须顶点在解空间所处的位置：

Xrl={(Xri,Xli)|i∈[1,n]}

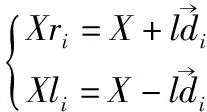
(6)

其中，X是天牛质心的位置，Xrl是每对左右触须顶点的位置，Xri和Xli分别是第i对左右触须顶点的位置，l是质心到天牛触须顶点的距离长度.特别说明，天牛质心一般取天牛头部中间位置，即两触须的中间位置.

3.1.2 变步长的探路反馈更新策略

传统BAS算法中个体的位置更新只在两个感知方向上，并且不论更新后的新位置优劣如何，都将作为新一代个体参与下次操作，假设更新后的个体比更新前的个体差，则算法会演变为向背离全局最优解的方向搜索，因此，一种变步长的探路反馈更新策略被提出用来解决这一难题.首先，天牛个体通过式(7)以步长δ在多向感知模型产生的n对左右触须方向上进行更新，并得到n个反馈个体的位置Xf，然后在n个反馈个体中选取最佳个体用与当前个体进行比较，如果前者优于后者，则将最佳个体替代当前个体，反之，仍然采用当前个体参与下一轮操作.

(7)

这种通过事先探路式的更新和比较可以有效的增强局部搜索能力，但这可能产生一个问题，如果当前个体经比较后不采取位置的更新，而δ和l经过很多代的不断缩小后变的不足以使当前个体探索更广泛的空间，这会导致当前个体容易持续多代保持不更新的状态.基于以上考虑，本文设计如图2所示的δ和l的更新规则.

图2 参数更新规则流程图

如果当前个体进行了更新操作，说明在当前参数δ和l的作用下是可以继续寻找最优解的，则δ和l两个参数都不更新；如果当前个体没有进行更新操作，说明在当前个体附近有很大概率并不存在比当前个体位置更好的位置了，当然，这并不排除没有发现个体周围更好的位置的情况，所以用一个很小的排除概率pe来表示当前个体周围还有更好的位置没有被发现，所以δ和l在这种情况下依旧不采取更新措施，抛开这种特殊情况，则需要通过式(8)来更新δ和l来改变感知范围，以找到更好的位置解.

lt=0.95lt-1+0.01

δt=0.95δt-1

(8)

其中，t是当前迭代次数.

3.2 改进的GA算法

3.2.1 扩展的多子代竞争杂交算子

在GA中，交叉算子负责探索新的解，组合产生新的个体，尤其在后期种群个体同类化严重的状况下，交叉对维护种群的多样性起到了重要的作用.假设求解问题维度为2，基本整体算术交叉如图3(a)所示，两父代个体产生的子代只能在父代之间的解区域内产生，这不利于充分挖掘父代的优质基因.为了能够对父代个体周围区域进行短距离的探索，有研究采用了扩展的算术交叉方法[16]，通过改变算术交叉中的随机数范围使子代个体能够跳出父代个体围成的解区域.例如，将式(1)中的随机数范围从0到1扩展为从-0.5到1.25，从图3(b)可以看出，改进后的子代分布不再被局限于父代解空间之间，而是随机分布在父代周围.

图3 交叉示意图

上述改进虽然让子代具有了较为活跃的分布，但如果两父代差异过大，那么子代将分布于广泛的解空间范围内，在一定程度上将增加算法的随机性.并且，子代的产生只与两个父代有关联，而与种群其他个体无关，抛开遗传学说，从种群进化角度来看，这种封闭式的进化从本质上弱化了种群之间相互学习的优势，不利于群体的进化.因此，本文在前人的扩展交叉方法的基础上提出了一种差分多子代竞争交叉策略，首先让父代按照扩展算术交叉的方式产生两个子代，然后让父代与种群其余两个个体通过差分操作再次产生两个子代，比较4个子代的优劣，取最优的两个子代作为新的个体参与算法下一步的操作.综上，本文的交叉方式将按照式(9)进行操作：

(9)

其中，Xc是子代个体，Xf是父代个体.Xi和Xj是种群中与父代个体互不相同的两个个体.r是随机数，将通过式(10)加以描述.

(10)

通过上述的差分多子代竞争交叉方式，产生的子代既可以充分挖掘父代周围的信息，又可以增强种群个体间优质基因的交互性.

3.2.2 交叉概率和变异概率的自适应改进

交叉概率(pc)和变异概率(pm)是影响算法挖掘与探索平衡的关键参数.传统GA采用固定的pc和pm取值，但取值不易控制，如果取值过大，会增加算法的随机性，反之，会影响算法的收敛能力.为此，不少学者提出了自适应改变pc和pm的方法，并取得了一定的效果[17,18].本文采取一种非线性自适应调节pc和pm的方法来缩减交叉和变异的频率，进而调控种群个体对解空间的搜索频率.自适应调节pc和pm的具体公式见式(11)，这一改进方法已经在本文作者之前所发表的文献[19]中进行了报道，因此不再进行详述.简单来说，如图4(a)所示，在进化前期交叉概率较大，能够有效提高前期种群物种丰富程度，而在进化接近结束时，交叉概率变小，能够提高算法的收敛能力.自适应调节pm的具体公式如式(12)所示，图4(b)中实体曲线表示pm的取值，从该曲线可以看出，个体适应度会随着(f-favg)的增大而减小，这种变化规律很好的保护了优质个体.

(11)

其中：A是控制曲线曲率的参数，g是当前进化代数，G是总进化代数，pcmax是最大交叉概率，pcmin是最小交叉概率.

(12)

其中，fmax和favg分别是种群最大个体适应度和平均适应度，f是种群当前个体适应度，pmmax和pmmin分别是最大和最小变异概率.

图4 交叉示意图

3.3 混合策略

BASGA算法采用一种简单的混合策略，将改进后的BAS算法加入到改进后的GA算法中对每代初始种群的个体进行BAS操作，成为改进GA种群适应度的一个算子.在算法的前期阶段，个体间的差别较大，执行改进BAS算法时，优质个体只需执行很少次迭代便可达到预期效果，而劣质个体则需要执行较多次迭代，因此改进BAS算法的迭代次数采用固定值是不合理的，应根据个体的优劣程度进行区别对待.此外，本文在改进BAS算法中通过相邻代最优个体(Xbest)的适应度差值来判断算法是否可以停止，如果该差值连续很多代(伪代码中设置为ξ代)都小于一个设定的数值ε，则认为算法很难再寻优下去，即算法终止.具体判断规则按照以下算法1所示的伪代码进行：

算法1.BAS算法终止规则伪代码

1.t=0

3.t=t+1

4. Ift>ξ

5. 算法终止

6.end

另外，如果改进GA中种群所有个体都参与改进BAS算法会过早降低种群的多样性，因此参与改进BAS运算的个体数量被设定为种群规模的10%.

3.4 BASGA算法的流程

通过对上述算法的描述，给出本文算法的流程图和实现步骤，如图5所示.

图5 BASGA算法流程图

BASGA算法实现步骤如下：

步骤1.设定算法初始参数，包括种群规模、维度和天牛须搜索算法需要的参数并生成初始种群；

步骤2.计算种群个体的适应度值，根据适应度值确定全局最优个体；

步骤3.种群个体优劣的评价.计算种群个体的适应度值；

步骤4.从种群中选出规定数量的个体参与改进BAS算法的操作；

步骤5.根据式(5)和式(6)建立多向感知模型，计算各方向上感知触须所处的位置；然后个体进行基于反馈策略的位置更新，并且更新步长和质心到触须的长度；

步骤6.判断是否满足改进BAS操作的结束条件，如果满足结束条件则转入步骤7；反之，转入步骤3；

步骤7.种群进行遗传操作，分别参与选择操作、交叉操作和变异操作；

步骤8.判断是否满足改进GA的结束条件，如果满足，则输出最优个体和最优解；反之，转入步骤2.

4 仿真实验与结果分析

4.1 测试函数及对比算法

为了测试本文提出的BASGA算法的性 能，对表1给出的12个标准测试函数进行了仿真实验，其中，单峰值测试函数(f1～f6)用来测试算法挖掘群体信息的能力(称为开采能力)和收敛精度,多峰值测试函数(f7～f12)用来测试算法探寻种群之外其他信息的能力(称为勘探能力)和解决复杂优化问题的能力.本节选取近年来新提出的BASFPA和IGPSO[20]两种混合算法作为对比算法，其中BASFPA算法是天牛须搜索算法与花朵授粉算法的混合，该算法依靠天牛须搜索算法来加快花朵授粉算法的收敛速度，具有较好的收敛效果;IGPSO算法是遗传算法与粒子群算法的混合，具有典型性.

表1 标准测试函数

Table 1 Standard test functions

函数名字搜索范围最优值f1.Sphere[-100,100]D0f2.Tablet[-100,100]D0f3.DeJong[-100,100]D0f4.Schwefel1.2[-100,100]D0f5.Easom[-10,10]D-1f6.Sumofdiff.power[-100,100]D0f7.Girewank[-600,600]D0f8.Ackley[-32,32]D0f9.Alpine[-10,10]D0f10.Giunta[-10,10]D0f11.Salomon[-100,100]D0f12.Noncont_Rastrigin[-5.12,5.12]D0

实验选取了3个指标评价算法的性能：1)均值(Mean)，该指标是算法多次运行的最优适应度的均值，反应求解质量的好坏，均值越小，说明算法结果越好;2)标准差(Std)，该指标是实际最优值与均值之间的标准差，能够反应算法求解的稳定性，Std越小，则算法的稳定性越好;3)成功率(SR)，该指标是函数被求解成功的次数占总执行次数的比值，其中，函数求解成功是指求解结果优于指定的求解精度(12个测试函数在不同维度下的求解精度标准在表2中均有设置).

4.2 仿真实验与结果分析

为了公平起见，在算法参数设置上，BASFPA算法和IGPSO算法的参数与原文献保持一致(种群规模N除外)，详细参数可以参考相应文献.三种算法都采用实数编码，种群规模为60，运行代数都为200代.本文提出的BASGA算法采用高斯变异[21]和保留最佳个体的选择方法[22]，相关参数设定为：触须感知方向数量n=5，排除概率pe=0.05，初始步长δ=5，质心到触须距离初值l=0.5，A=10，pcmin=0.6，pcmax=0.9，pmmin=0.01，pmmax=0.1，ξ=10，ε=10-3.

实验将分为两个部分进行：一是单峰值函数的优化，待求解问题的维度被设定为10维、30维和60维(除函数f5维度为2、5和10外).二是多峰值函数的优化，将分别从5维、15维和30维进行求解.所有测试在Windows10操作系统，MATLAB2016b仿真平台上进行.每种算法独立运行30次，记录均值、方差和成功率.

表2 函数不同维度下的求解精度

Table 2 Solving accuracy of functions in different dimensions

函数维度D=10D=30D=60函数维度D=5D=15D=30f110-810-610-4f710-810-610-3f210-810-510-2f810-510-310-1f310-810-610-4f910-510-1100f410-810-410-1f1010-310-210-1f∗510-5(D=2)10-2(D=5)10-1(D=10)f1110-210-1100f610-1010-710-4f1210-2100101

说明：因为函数f5的数学特性导致最小值不容易求解，维度的增高会加大算法的求解难度，因此求解维度不宜过高，分别设置为2、5和10.

4.2.1 单峰值函数优化下的性能分析

表3给出了3种算法对6个单峰测试函数的优化结果对比.在收敛成功率上，BASFPA算法经常出现SR为0的情况，说明了该算法的收敛能力是这三种混合算法中最差的.BASGA算法在整体上都有不错的收敛成功率，尤其是对函数f2特定10维和30维的优化上，成功率相比其余两个算法要高很多，说明该算法具有更强的收敛能力和寻优能力.从均值的对比来看，BASGA算法整体上要好于其他两种算法，而IGPSO算法要好于BASFPA算法.尤其是在对函数f3特定30维和60维的优化上，BASGA算法的寻优精度接近10-15，远远超过了其他两种算法，特别地，函数f5的数学特性类似广袤平原中的一口水井，解空间内的域值相似度较高，会对算法寻优造成方向上的干扰，从表3对该函数的优化数据可以看出，三种算法在10维下都没有寻找到最优解，但是在2维的优化中，BASGA算法寻找到了理论最优值，而IGPSO和BASFPA算法虽然寻找到了函数域值的下降区域，但是并没有继续搜索下去，这也说明两种算法的搜索能力较BASGA算法偏弱.

从表3标准差的对比中可以看出算法IGPSO的Std值与其对应均值之间有相对明显的差距，而BASGA算法和BASFPA算法的Std值与其对应Mean值之间的差距相对较小.在对函数f2特定30维和60维的优化中，IGPSO算法的Std值与其Mean值之间的差距尤其明显，说明该算法每次运行后的结果波动较大，稳定性较差.反观BASGA算法的Std值与其均值之间的差距均保持在10-1个精度之内，稳定性要强于其余两种算法.

为了更加直观的反映算法的收敛速度，给出了函数f1～f12在特定维度下的收敛曲线对比图.从图6(a)-图6(f)中可以看出，BASGA算法在单峰值函数优化中相比于其余两种算法具有更快的寻优速度和更高的收敛精度，而BASFPA算法从整体上看表现最差，尤其是函数f5的收敛曲线，BASGA算法一开始就表现出了很好的收敛能力，在不足40代内就达到了规定的求解精度，IGPSO算法虽然也达到了精度要求，但与前者算法相比收敛较为缓慢，而BASFPA算法在后期的表现最差.

表3 三种算法对测试函数f1～f6的寻优结果比较

Table 3 Comparisons of three algorithms for optimizing test functionsf1～f6

函数维度BASFPAMeanStdSRIGPSOMeanStdSRBASGAMeanStdSRf1104.77E-056.90E-0602.29E-099.63E-0993%3.75E-138.12E-13100%303.36E-049.4059E-0405.76E-068.64E-0639%8.4394E-091.3214E-09100%605.39E-017.68E-0208.97E-067.81E-0696%3.29E-077.10E-07100%f2103.98E+012.54E+0001.16E-056.89E-058%8.20E-084.53E-0873%302.81E+033.49E+0202.49E-031.28E-033%1.23E-057.35E-0548%607.16E+038.41E+0201.91E-021.87E-0259%4.04E-021.41E-0255%f3101.44E-059.55E-0627%9.79E-163.85E-17100%2.57E-217.25E-22100%302.64E-014.43E-0204.64E-064.94E-0665%1.80E-141.31E-15100%607.29E+012.68E+0106.32E-018.15E-0204.53E-137.88E-13100%f4107.24E-044.16E-0402.46E-065.25E-0633%2.56E-096.54E-0971%302.94E-035.94E-0402.69E-016.26E-0202.43E-068.47E-06100%607.70E+017.81E+003%1.56E-023.57E-0261%1.03E-049.25E-04100%f521.00E-041.96E-0439%2.39E-147.49E-12100%0.00E+001.22E-14100%59.92E-018.01E-0209.91E-015.44E+0009.90E-016.88E-019%101.00E+009.01E-0101.00E+009.13E-0101.00E+007.43E-010f6101.64E-032.78E-0401.01E-077.28E-0810%5.37E-144.00E-15100%302.00E-035.50E-0307.40E-067.69E-0640%1.39E-121.27E-1294%601.74E+036.48E+0208.00E-049.14E-0487%7.80E-125.31E-13100%

4.2.2 多峰值函数优化下的性能分析

表4是6个多峰函数的优化结果，通过对比分析，在寻优精度上，BASGA算法不论低维和高维都要好于其他两种算法，尤其是在低维优化中表现出了很好的寻优性能.特别是在f8的优化中，BASGA在15维下的均值精度是10-5，远远好于其余算法.在收敛成功率方面，三种算法都容易出现很高成功率和很低的成功率两个极端，通过对函数f11结果的分析可知，当维度为15和30时，BASGA算法的SR都是100%，其余算法的SR为0，说明BASGA算法在30次实验中每次都能跳出局部极值进而收敛到规定的精度范围之内，而其余两种算法因为陷入局部最优解而无法达到规定的收敛精度.

从图6(g)-图6(l)可以看出，BASGA算法在多峰值问题求解中也有很好的搜索性能，根据函数f7的优化曲线可知，IGPSO算法在60代之前其收敛曲线下降非常快，但在60代之后曲线呈持平状态，该算法的特点是前期有很好的收敛性能，但中后期容易陷入局部最优值的僵局，反观BASGA算法虽然前期下降缓慢，但中后期开始快速收敛，表明BASGA算法能够保持良好的多样性，在复杂的多峰问题中也有良好的寻优能力.

表4 三种算法对测试函数f7～f8的寻优结果比较

Table 4 Comparisons of three algorithms for optimizing test functionsf7～f8

函数维度BASFPAMeanStdSRIGPSOMeanStdSRBASGAMeanStdSR52.33E-028.67E-0302.72E-092.30E-0950%1.90E-135.94E-14100%f7151.27E-054.15E-0542%1.27E-054.15E-0542%1.66E-096.59E-09100%301.11E+013.15E+0001.53E+021.68E+0101.15E-094.61E-10100%52.16E-013.15E-0203.61E-062.65E-0653%1.21E-062.10E-0691%f8158.59E-019.12E-0106.23E+001.44E-0104.71E-054.75E-05100%302.52E+005.40E-0101.7E+015.41E+0001.36E-049.50E-04100%54.23E-036.79E-0404.50E-068.15E-0784%7.63E-088.35E-09100%f9153.03E-015.79E-0162%1.08E+018.30E+00100%1.30E-034.40E-04100%302.56E+008.88E-0140%2.99E+019.45E+0005.32E-024.15E-03100%56.16E-026.28E-0303.58E-026.60E-0310%1.17E-035.95E-0483%f10154.92E-015.23E-0108.31E-013.71E-0130%3.52E-032.86E-0388%308.94E-012.75E-0250%9.38E+008.59E-0107.58E-023.07E-0390%51.00E-013.04E-0156%1.11E-012.53E-0250%9.98E-023.03E-02100%f11151.11E+009.31E-0105.71E+003.79E-0109.93E-024.92E-03100%302.29E+009.14E-0101.57E+012.66E+0001.99E-014.87E-02100%52.22E+008.96E-0102.00E-071.33E-07100%1.11E-079.89E-08100%f12152.70E+011.88E+0104.85E+008.16E+0056%6.00E+009.21E-0179%307.99E+17.11E+0001.52E+024.01E+0101.30E+013.35E+0031%

图6 三种算法的寻优曲线对比

5 结 论

针对遗传算法和天牛须搜索算法的优缺点，本文从扬长避短的思想出发，率先提出了两种算法混合的优化算法(简称BASGA算法)，该算法通过建立多向模型和反馈更新策略来提高算法的局部搜索能力和寻优速度，本文还将交叉算子进行了扩展改进，并动态的改变交叉和变异参数值，使算法能够在复杂的多峰问题中也具有较好的全局寻优能力.函数优化实验证明，BASGA算法能够很好的克服天牛须搜索算法后期的陷入局部极值问题和遗传算法收敛过慢的缺点，具有较好的处理单、多峰值优化问题的能力.