融合多元异构信息的矩阵分解推荐算法
2020-07-13王根生潘方正
王根生,潘方正
1(江西财经大学 人文学院,南昌 330013) 2(江西财经大学 计算机实践教学中心,南昌 330013) 3(江西财经大学 国际经贸学院,南昌 330013)
1 引 言
推荐算法是解决信息过载问题的一种重要技术,在电子商务、网络媒体、新闻广告等领域得到了广泛应用.目前推荐算法主要分为3类:基于内容过滤推荐、协同过滤推荐和混合推荐[1].协同过滤推荐算法是目前应用最为广泛的一类算法[2],其主要分为基于用户(User-based CF)的协同过滤、基于物品(Item-based CF)的协同过滤和基于模型(Model-based CF)的协同过滤[3].基于模型的协同过滤使用机器学习的算法思路进行建模[4],矩阵分解就是一种基于模型协同过滤的经典算法.矩阵分解推荐算法在Netflix百万大奖赛中脱颖而出后,成为当下十分流行的一种推荐算法.
虽然矩阵分解推荐算法相对其他协同过滤算法能取得更好的推荐效果,但依然面临数据稀疏和不能反映用户兴趣变化的问题.针对这些问题国内外不少学者提出了相关改进方案,如针对数据稀疏问题:文献[5]提出了一种基于属性耦合的矩阵分解方法,将物品属性信息融入到矩阵分解模型中;文献[6]在利用显式评分信息的基础上,引入其他的隐式信息(如浏览、收藏和分享等);文献[7]利用社交网络信息计算用户的社会地位,把用户的社会地位融合到矩阵分解推荐算法之中;文献[8]提出一种融合社交网络和用户间的兴趣偏好相似度的正则化矩阵分解推荐算法.针对用户兴趣变化的问题:文献[9]利用时序图区分用户的长期兴趣和短期兴趣;文献[10,11]在协同过滤算法中分别引入了时间衰减模型和艾宾浩斯遗忘曲线来适应用户兴趣变化;文献[12]利用时间窗口动态计算电影相似度,缓解用户兴趣变化问题.
通过分析发现,目前加入其他辅助信息是缓解数据稀疏的主要思路,引入时间窗口、遗忘曲线、长短期兴趣模型是反映用户兴趣变化的主要思路.随着互联网的快速发展,数据呈现多元性和异构性,如何整合这些多元异构数据对提高推荐算法的性能有重要意义.所以本文提出一种融合用户点评数据、用户-物品评分数据、物品异构信息和遗忘曲线改进的矩阵分解推荐算法,缓解数据稀疏的同时解决用户兴趣变化的问题.
2 相关工作
2.1 矩阵分解推荐算法
矩阵分解推荐算法(FunkSVD)的基本思想是把用户-物品评分矩阵R分解成两个低维的用户特征矩阵U和物品特征矩阵V,如公式(1)所示.
R≈UVT
(1)
其中,V∈Rn×d,m和n分别代表用户和物品的个数,d为用户和物品特征维度.利用矩阵U和V去拟合用户对物品的评分,并对未评分物品进行预测.为了使公式(1)最大程度拟合用户-物品的真实评分数据,使用线性回归的思路,建立目标优化函数,具体如公式(2)所示.
(2)

随着研究的深入,学者们提出了不少改进型矩阵分解模型,比如联合矩阵分解、概率矩阵分解模型等.联合矩阵分解通过分解多重相关联矩阵来缓解矩阵分解中数据稀疏的问题,这些多重相关联的矩阵包含相同的实体,可以从包含相同实体的关系矩阵中获取更多额外的信息[13].
2.2 Word2vec
Word2vec基于深度学习把词语映射到包含语义关系的低维实数空间,语义相似的词语在这个空间中也相近[14].Word2vec改变了传统one-hot编码向量维度高、矩阵稀疏、语义缺失的问题,被广泛运用于自然语言处理中.Word2vec包括Skip-Gram和CBOW两种训练模型,Skip-Gram通过输入词wt来预测其上下文Swt=(wt-k,…,wt-1,wt+1,…,wt+k),其中k为wt上下文窗口大小.CBOW则是根据上下文Swt去预测wt,其目标优化函数分别如公式(3)和公式(4)所示.
(3)
(4)
2.3 异构信息网络
异构信息网络(heterogeneous information network, HIN)是包含多种类型节点和边的信息网络[15].HIN=(V,E,A,R),其中V代表顶点集、E代表边集、A代表顶点类型、R代表边类型,|A|>1或者|R|>1,存在映射φ:V→A,φ:E→R.加权异构信息网络(weighted heterogeneous information network, WHIN)在HIN的基础上加入连接权重W,WHIN=(V,E,W,A,R),W代表连接权重,存在映射γ:E→W.图1为一个典型的WHIN网络模式实例图.

图1 加权异构信息网络的网络模式实例图
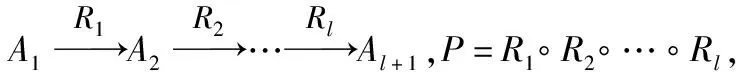
3 融合多元异构信息的矩阵分解推荐算法
本文算法的主要思路是从用户点评数据和物品异构信息中挖掘物品相似度矩阵和用户兴趣相似度矩阵,并在用户兴趣表示中引入遗忘曲线,适应用户兴趣变化.然后把物品相似度矩阵和用户兴趣相似度矩阵融合到传统矩阵分解的目标函数中,得出用户特征矩阵和物品特征矩阵,预测用户对物品的评分,完成推荐.
3.1 物品相似度矩阵计算
物品相似度的计算依赖于对物品的特征描述,如何获得对物品内容的精准描述成为一个关键,这也是基于内容过滤推荐的核心.在很多推荐领域,我们无法直接获取物品内容的描述,如电影推荐,目前其相似度的计算大部分基于电影的属性信息(如类型、主演、导演等).而随着在线影评网站的发展,每部电影都积累了大量的用户点评数据,通过文本分析技术可以从这些点评数据中挖掘出电影的内容信息.所以本文以电影推荐为例,结合电影属性信息和点评数据计算电影的相似度,算法流程如图2所示.
3.1.1 电影内容相似度
对所有点评数据集进行分词,并对代词、连词、介词等相关停用词进行删除;利用Word2Vec模型进行训练,得到包含语义关系的词向量;使用TextRank算法对每部电影的关键词进行提取.TextRank[17]是根据PageRank算法改进而来,该算法广泛用于文本的关键词和关键词组的提取.如对电影《芳华》提取的影评关键词为“集体主义 战争 芳华 冯小刚 七十年代 信仰 残酷…”.得到代表电影mi内容的关键词组Wmi={w1,w2,…,wn}后,结合词向量,把Wmi中的每个关键词wn替换成对应的词向量Vwn=[v1,v2,…,vk],k为词向量的维度,Wmi={Vw1,Vw2,…,Vwn}.电影mi和mj的内容相似度计算如公式(5)所示.

图2 物品相似度矩阵计算流程
(5)
其中,n和m分别代表电影mi和mj关键词组的长度,cos(Vwi,Vwj)为词向量Vwi和Vwj的余弦相似度.
3.1.2 电影属性相似度
文献[18]提出了比较详细的电影属性相似度计算方法,电影的属性p={类型、上映国家、主演、导演、上映时间、获奖情况、标签、评分}.电影mi和mj的属性相似度计算如公式(6)所示.
(6)
其中,sim(pi)表示两部电影在第i个属性上的相似度,wi为第i个属性的权重.具体每个属性的相似度sim(pi)的计算和权重wi的计算参考文献[18].
3.1.3 电影相似度
得到电影内容相似度Sc(mi,mj)和电影属性相似度Sp(mi,mj)后,把二者进行融合,得到电影整体相似度,融合计算如公式(7)所示.
S(mi,mj)=βSc(mi,mj)+(1-β)Sp(mi,mj)
(7)
其中,β为融合权重,控制电影内容相似度和电影属性相似度对电影整体相似度的影响比例.利用公式(7)计算所有电影的相似度,得出电影相似度矩阵D.
3.2 用户兴趣相似度矩阵计算
通过用户-物品评分数据、物品异构属性信息和遗忘曲线构建用户-物品-属性的加权异构信息网络;在网络中选择连接用户的相关元路径,并计算不同元路径的权重;计算不同元路径下的用户兴趣相似度,结合元路径权重得出最终用户兴趣相似度,算法流程如图3所示.
3.2.1 用户-物品-属性加权异构信息网络构建
以电影为例,用户-电影-属性异构信息网络中V={电影(Movie)、用户(User)、主演(Actor)、导演(Director)、类型(Genre)、国家(Country)、编剧(Screenplay)},E={评分/被评分、演绎/被演绎、导演/被导演、属于/包含、所属/包含、编写/被编写},具体网络模式可见图1.确定了网络中的实体和关系后,重点是如何计算网络中的连接权重W.目前用户-电影的连接权重基本上都直接使用用户对电影的评分,如文献[19,20],评分1-5分别对应了{非常不喜欢、不喜欢、一般、喜欢、非常喜欢}五种情况,但这种方式有如下问题:首先,使用连续的数字 1-5 很难体现兴趣的正反变化(不喜欢<3,喜欢>3)和兴趣的非线性变化差异(非常喜欢与喜欢的差别和一般与不喜欢的差别是不一样,应该是中间变化大,两头变化小);其次,没有体现用户兴趣随时间的变化,随着时间的推移,用户的兴趣可能会逐渐改变,所以历史数据具有保鲜度,时间越长的数据越难反应用户当前的兴趣情况.针对这两点提出基于神经网络激活函数tanh和遗忘曲线改进的权重计算,计算如公式(8)所示.
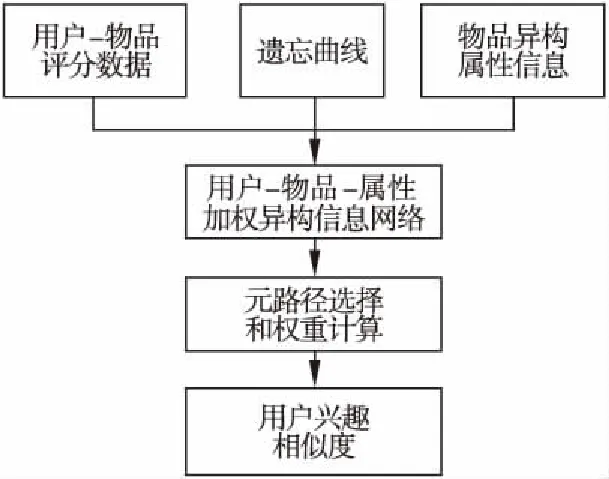
图3 用户兴趣相似度矩阵计算流程
wu_m(s,t)=tanh(s)*memory(t)
(8)
其中,wu_m(s,t)代表用户u对电影m的兴趣连接权重,s为用户u对电影m的评分,t为评论间隔时间(天).tanh(s)为激活函数,其函数公式如式(9)所示.memory(t)为遗忘曲线函数,本文选取文献[21]对艾宾浩斯遗忘曲线拟合函数,其函数公式如式(10)所示.
(9)
memory(t)=31.8*t-0.125
(10)
网络中其他关系,如:电影与类别、电影与国家、电影与编剧、电影与导演,为单值关系,权重设为1,而电影和主演间的权重可以根据主演的排序决定,取排序的倒数.
3.2.2 元路径选择和权重计算
不同的元路径蕴含了不同的语义信息,本文选择了6条元路径,具体说明见表1所示.
不同元路径下得出的用户兴趣相似度的置信度是不一样的,随着路径的变长,置信度也越低,就好比人际关系网络,随着关联路径的变长,之间的信任关系也逐渐降低.基于这个事实,文献[20]提出一种基于元路径长度的权重计算方法.但这个方法主要有2个问题:1)没有对同长度的元路径做权重区分,电影的类型、主演、导演、上映国家、编剧对影响用户对该电影的喜爱程度是不一样的;2)没有对不同用户做区分,因为同一特征对不同用户的影响也是不一样的.所以本文提出一种基于信息增益改进的算法,算法步骤如下:
Step 1.把每个用户评价过的电影分成喜欢(评分>3)和不喜欢(评分<3)两类,用Ci表示.
Step 2.把类型、主演、导演、上映国家、编剧作为影响用户对电影态度的特征T,并根据信息增益IG(T)算法计算每个特征的影响程度,计算如公式(11)所示.
表1 电影推荐异构信息中典型的元路径及其语义
Table 1 Typical meta path and its semantics in heterogeneous information of movie recommendation

元路径语义信息P1=User-Movie-User两用户评分过同一部电影P2=User-Movie-Genre-Movie-User两用户评分过属于同一类型下的两部电影P3=User-Movie-Actor-Movie-User两用户评分过属于同一演员主演的两部电影P4=User-Movie-Director-Movie-User两用户评分过属于同一导演执导的两部电影P5=User-Movie-Country-Movie-User两用户评分过属于同一国家上映的两部电影P6=User-Movie-Screenplay-Movie-User两用户评分过属于同一编剧编制的两部电影
(11)
Step 3.结合路径长度和特征信息增益,计算不同用户间的元路径权重,计算如公式(12)所示.
(12)
其中,wPl(ui,uj)表示对于用户ui和uj来说元路径Pl的权重,T表示元路径Pl中连接用户的某个电影特征,len(Pl)为路径长度,IGui(T)和IGuj(T)分别为用户ui和uj的特征T的信息增益.
3.2.3 用户兴趣相似度计算
本文使用PathSim[22]算法计算元路径中同类型节点的相似度,算法如公式(13)所示.
(13)
其中,Wi,j表示在元路径Pl下用户ui到uj所有路径实例的连接权重之和.在得出不同元路径下的用户相似度后,结合元路径权重,综合所有元路径下的用户相似度,计算如公式(14)所示.
(14)
其中,P为元路径集合,wPl(ui,uj)为对于用户ui和uj来说的元路径Pl的权重,其计算见公式(12).利用公式(14)计算所有用户间的兴趣相似度,得出用户-用户兴趣相似度矩阵S.
3.3 融合矩阵分解
将用户兴趣相似度矩阵S、电影相似度矩阵D和用户-物品评分矩阵R进行联合分解,融合多元异构信息得出用户和物品的特征矩阵,弥补单一信息可能存在的数据稀疏和局部性问题.融合矩阵分解的目标函数如公式(15)所示.
(15)
其中,U为用户特征矩阵、V为物品特征矩阵、Z为用户兴趣相似特征矩阵、H为物品相似特征矩阵、Iik为指示参数.g(Ri,j)=(Ri,j-min)/(max-min)把评分归一化,和用户兴趣相似度矩阵S和物品相似度矩阵D的取值范围保持一致.λ1、λ2是平衡系数,平衡用户兴趣相似度和电影相似度的影响,如果二者都为0,算法退化为只利用了评分信息的传统矩阵分解算法.使用梯度下降法进行目标优化函数(15)进行求解,具体迭代过程如公式(16)-公式(23)所示.
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
其中α为学习率.得出用户特征矩阵U和物品特征矩阵V后,利用公式(24)预测用户i对物品j的评分,把大于某阈值的预测评分物品推荐给用户,完成推荐.
(24)
其中,max为公式(15)中g(Ri,j)中进行归一化的评分最大值,min为评分最小值,公式(24)为归一化的反过程.
4 实验及分析
4.1 实验数据
本实验数据集来源于网络爬虫爬取的豆瓣影评数据,爬取的原始数据为94534个用户对8872部电影的404972条评价,数据的稠密度为0.048%,考虑到原始数据太过于稀疏,所以只保留评论和被评论不少于10次的用户和电影,最终得到7815个用户,1593部电影,214920条评论作为实验数据,数据稠密度为1.73%,介于数据集MovieLens1M(稠密度为4.3%)和MovieLens10M(稠密度为1.2%)之间.存储实验数据的主要表结构如表2、表3所示.
表2 评论表结构
Table 2 Comment table structure

字段说 明Id主键Timestamp评价时间MovieId被评论电影IdRating评分Content评论UserId评价用户Id
表3 电影信息表结构
Table 3 Movie information table structure

字段说 明Id主键Name片名DirectorId导演imdb编号ActorIds主演imdb编号,多个主演用逗号隔开Country制片国家ScreenwriterIds编剧imdb编号,多个编剧用逗号隔开Genres类型,多种类型用逗号隔开ReleaseDate上映日期
4.2 评价指标
本实验使用预测评分与实际用户评分的均方根误差(RMSE)、准确率(Precision)、召回率(Recall)和覆盖率(Coverage)四个指标进行算法性能衡量,四者的计算分别如公式(25)-公式(28)所示.
(25)
(26)
(27)
(28)
表4 混合矩阵
Table 4 Mixed matrix

推荐算法用户喜爱用户不喜爱推荐TPFP未推荐FNTN
公式(28)中N为测试数据集T中不同电影总个数,Nd为推荐结果中不同电影总数目.覆盖率越高说明推荐结果具有多样性和新颖性.
4.3 实验结果及分析
为了对算法的性能进行更精准的衡量,本文使用k-交叉验证的方式进行验证,k值取5,即随机把试验数据均分成五份,每次挑选其中一份作为测试集,其他4份作为训练集,一共进行5次测试,使用5次测试的平均值作为算法最终评价.实验主要参数及其默认值如表5所示.
表5 实验参数设置
Table 5 Setting of experimental parameters

参 数默认值TextRank提取关键词组长度20Word2vec词向量维度k100电影相似度融合系数β0.6融合矩阵分解平衡系数λ11融合矩阵分解平衡系数λ22正则化参数λ31e-3梯度下降学习率α1e-2梯度下降迭代次数300用户和电影特征维度d25推荐阈值预测评分4
1)不同用户和电影特征维度下的实验对比
矩阵分解时需要设定用户和电影的特征维度d,不同的维度值下可能会得到不同的实验结果.本实验设置维度d={10、15、20、25、30、35、40、45、50},共9组实验进行对比,其他参数和表4保持一致,实验结果如图4所示.

图4 不同用户和电影特征维度下的实验结果对比
通过实验发现,当用户和电影维度为25时,算法的RMSE、准确率、召回率、覆盖率相对较好.
2)不同平衡系数值的实验对比
公式(15)中的融合矩阵分解平衡系数λ1和λ2分别控制用户兴趣信息和电影相似度信息对结果的影响比例,本次实验设置a(λ1=0,λ2=0)、b(λ1=0,λ2=1)、c(λ1=1,0)、d(λ1=1,λ2=1)、e(λ1=1,λ2=2),f(λ1=2,λ2=1)共6组实验进行对比,其他参数和表4保持一致,实验结果如图5所示.
通过实验发现,a组相对其他5组的准确率、召回率、覆盖率最低,RMSE值最高.a组λ1和λ2都为0,算法退化为传统的矩阵推荐算法,其他五组都在传统的矩阵推荐算法中融入了用户兴趣信息或电影相似度信息,证明融入相关辅助信息可以改进传统矩阵推荐算法.同时融入了用户兴趣信息和电影相似度信息的d、e、f三组实验结果优于只融入了其中一种信息的b、c两组实验结果.在d、e、f三组实验中e(λ1=1,λ2=2)组的准确率、召回率、覆盖最高,RMSE最低.
3)和其他算法对比
为了进一步验证本文算法的有效性,把本文算法(MHI_MF)和基于用户(UCF)的协同过滤、基于物品(ICF)的协同过滤、传统矩阵分解推荐算法(FunkSVD)、在本文算法基础上不考虑遗忘曲线memory(t)的改进算法(MHI_CF-m)、文献

图5 不同平衡系数组合下的实验结果对比

图6 不同算法间的实验结果对比
通过实验结果图6可以看出,FunkSVD相比于UCF和ICF两种协同过滤算法的性能指标要好,其他四种改进的算法(MHI_MF、MHI_CF-m、HIN_UCF、ICFUIC)相比于FunkSVD算法的性能指标更好,本文改进算法(MHI_MF)算法相比其他三种改进算法(MHI_CF-m、HIN_UCF、ICFUIC)的性能指标更好.HIN_UCF在协同过滤推荐算法加入了相关辅助信息但没有考虑用户兴趣的变化,ICFUIC考虑了用户的兴趣变化但没有引入其他的辅助信息,本文MHI_MF算法两者皆有考虑,说明了融合多元异构信息的有效性.而通过MHI_MF算法和MHI_CF-m的对比,近一步证明了本文算法引入遗忘曲线是有效果的.
5 结束语
传统矩阵分解的推荐算法为静态推荐模型,没有考虑用户兴趣随时间的变化,并且算法十分依赖评分数据的稠密度,当数据稀疏时算法效果不佳,而现实当中我们往往面临的数据又十分稀疏的.针对这两个问题,本文提出一种融合用户点评数据、用户-物品评分数据、物品异构信息和遗忘曲线的改进型矩阵分解推荐算法.通过融合多种异构信息缓解评分数据稀疏问题,并且增强了矩阵推荐算法的可解释性;通过遗忘曲线模拟人的心理学变化和数据的保鲜度,从而反映用户的兴趣变化.最后通过多组实验对比证明了本文算法的有效性.虽然本文对传统矩阵分解推荐算法进行了很好的改进,但依然存在不足,例如,当面对海量数据时,矩阵分解的效率低下,而随着互联网的快速发展,将来面临的数据越来越庞大,如何在海量数据中如何设计高效的推荐算法是进一步需要研究的方向.
