唯一5-列表可染的完全多部图的特征化
2020-07-10张胜丹王艳宁王妍妍
张胜丹,王艳宁,*,王妍妍
(1. 燕山大学 理学院,河北 秦皇岛 066004;2. 燕山大学 经济管理学院,河北 秦皇岛 066004)
0 引言
随着无线设备的日益增加,无线电频谱稀缺的现象出现了。为了提高无线电频谱利用率,人们使用认知无线电技术解决频谱分配的优化问题[1-2]。根据认知无线电的原理,每个二级用户具有其自己的可用频谱,为此,我们可以将频谱分配问题抽象为图的列表染色问题[3-5]。如图1所示,二级网络被抽象为图G=(V,E,L),其中顶点V表示无线用户(比如基站、WLAN等),边E表示顶点间的干扰,L表示可用频谱的集合,这就构成了一个图的列表染色模型。
Mahmoodian和Mahdian[6]提出了唯一列表染色概念。文献[7-8]完全刻画了唯一2-列表可染图。之后,围绕完全多部图,Ghebleh等[9]、何文杰等[10]展开了对其唯一3-列表可染性问题的研究,并实现了对唯一3-列表可染的完全多部图的特征化。王艳宁等[11]特征化了六部以上的唯一4-列表可染的完全多部图(除去有限的几个图)。文献[12-13]证明了完全多部图K1*r,(2k-3)和K1*(2k-3),r具有M(k)性质。为了进一步研究唯一k-列表可染的完全多部图,文献[14]研究了刻画唯一k-列表可染图的算法复杂度。文献[15]得到了唯一k-列表可染的完全多部图的列表的一些特征。文献[16]获得了平面图、边界图及正则图的唯一k-列表可染性的相关结论。随着k值的增大,刻画唯一k-列表可染图的难度也相应增加。迄今为止,在唯一5-列表可染的完全多部图的研究中,除文献[12]研究了特定结构的完全多部图的M(5)性质外,没有其它的研究结果出现。而较高值的唯一k-列表可染图的特征化具有更强的应用价值。

ⅠⅡⅢ—主要用户;圆圈—划分用户间干扰域;
1 2 3 4 5—二级用户;括号内字母—用户可用频谱
图1 二级网络的列表染色模型
Fig.1 The list coloring model of secondary networks
本文对完全多部图的唯一5-列表可染性问题进行了研究。首先,运用分类讨论的方法,得到两类具有M(5)性质的完全多部图。接着,结合排列组合知识,构造列表安排,证明了一些完全多部图是唯一5-列表可染图。最终,除有限的图外,特征化了至少有两部顶点数多于1的唯一5-列表可染的完全k(k≥9)-部图。
1 预备知识
定义1[6]如果对任一顶点ν∈V(G),存在一个k-列表L(ν),使得G有且仅有一个L-染色,则称图G是唯一k-列表可染图,简记为UkLC图。
定义2[7]对给定图G的任意一个k-列表L,如果图G必有0种或2种L-染色,称图G具有M(k)性质。即图G具有M(k)性质的充要条件为图G不是UkLC图。
定义3[7]若图G具有M(k)性质,并且它是唯一(k-1)-列表可染的,则称图G的m数为k,用符号m(G)表示。
涉及完全多部图时,本文用符号s*r表示r个s,例如K1*3,6表示K1,1,1,6。
在唯一列表可染图的研究中,已经获得了如下结论。
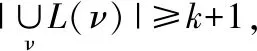
引理2[8]一个连通图具有M(2)性质当且仅当它的每个块或者是一个圈,或者是一个完全图,或者是一个完全偶图。
引理3[9]如果一个完全多部图G,其中包含一个是UkLC图的诱导子图,那么G也是UkLC图。
引理4[9]如果图G是完全多部图且G具有M(k)性质,则G的任意诱导子图也具有M(k)性质。
引理5[9]完全多部图K1*k,2*(k-1)的m数恒等于k+1。
引理6[11]对任意的r≥1,图K1*r,5具有M(4)性质,而且当r≥5时,m(K1*r,5)=4。
引理7[11]完全多部图K1*3,2,2,3,K1*4,2,2,2和K1*5,2,5是U4LC图。
引理8[11]对任意的r≥1,图K1*r,3,3具有M(4)性质,若r≥2,则m(K1*r,3,3)=4。
2 主要结论
定理1m(K1*6,3,3,3)=5。
证明:对图G=K1*6,3,3,3,它的前6部用Vi={νi},i=1,2,…,6表示,且后三部用Us={us1,us2,us3},s=1,2,3来表示。设对某一5-列表L,G有一个列表染色c。考虑图G后三部的染色情况。
1) 在{U1,U2,U3}中,至少存在一部Us使其满足|c(Us)|=1。
不失一般性,假设U1满足|c(U1)|=1。也就是说,U1中的所有顶点全染同一种颜色,记该颜色为a。从图G中移除U1,可得到新图G′=G-U1=K1*6,3,3。对任意ν∈G′,如果a∈L(ν),令L′(ν)=L(ν)
2) 在{U1,U2,U3}中,至少存在一部Us使其满足|c(Us)|=2。
不妨设U1满足|c(U1)|=2,则U1中一定存在染色相同的两个顶点,记该颜色为b。令X={u1i|c(u1i)=b,u1i∈U1,i=1,2,3},此时得到图G′=G-X=K1*7,3,3。对任意的ν∈V(G′),令L′(ν)=L(ν)
3) 任意s=1,2,3都有|c(Us)|=3成立。
在Us(s=1,2,3)的任意两点间都连接新边,则形成新图G′=K15。由引理2,完全图K15具有M(2)性质,且染色c是G′的一个L-染色,则G′存在另一个L-染色c′,由G′与G的关系知,c′也是G的一个新L-染色。
综上所述,图G具有M(5)性质。
由引理3和引理7知,图G=K1*6,3,3,3是U4LC图。因图G具有M(5)性质,则m(G)=5。
推论1对任意r≥3,图K1*r,3,3,3具有M(5)性质,且m(K1*r,3,3,3)=5。
证明:与定理1的证明方法类似,分析图K1*r,3,3,3的后三部分顶点染色情况,可得到图K1*r,3,3,3具有M(5)性质。由引理7知,图K1*3,2,2,3是U4LC图,那么当r≥3时,图K1*r,3,3,3也是U4LC图。则m(K1*r,3,3,3)=5。
定理2对任意r≥1,图K1*r,3,5具有M(5)性质,且当r≥5时,m(K1*r,3,5)=5。
证明:对图G=K1*r,3,5,它的前r部用Vi={νi},i=1,2,…,r表示,最后两部依次用U={u1,u2,u3}和W={w1,w2,w3,w4,w5}表示。设对某一5-列表L,G有一个L-染色c。下面对U部顶点的染色情况进行讨论。
1)U部至多染2种颜色。
由于U部至多染两种颜色,那么有两个顶点或者三个顶点染相同颜色。记该颜色为a,令X={ui|c(ui)=a,ui∈U,i=1,2,3},得到图G′=G-X,且G′是K1*(r+1),5的一个子图。对G′的任意一个顶点ν,令L′(ν)=L(ν)
2)U部染3种颜色。
在U部任意两点间都增加新边,形成新图G′=K1*(r+3),5。由引理6知,图G′具有M(4)性质,且已有染色c是G′的关于L的正常染色,则在G′上可得到另一个L-染色c′,显然c′也是G的一个新L-染色。
综上所述,图G=K1*r,3,5具有M(5)性质。
当r≥5时,依据引理3和引理7,图K1*r,3,5是U4LC图,则m(K1*r,3,5)=5。
定理3图K1*5,2*4,K1*6,2,2,4,K1*7,4,6,K1*7,5,5和K1*7,2,14是U5LC图。
证明:1) 首先,一个图G是UkLC图的充分必要条件是k 2) 对图G=K1*6,2,2,4,图G的9部分由{νi},i=1,2,…,6,{ν7,u7},{ν8,u8},{u1,u2,u3,u4}依次表示。给出图K1*6,2,2,4的5-列表分配如下: L(νi)={i,7,8,9,10},i=1,2,…,6, L(ν7,u7)={4,6,7,8,9;1,2,3,5,7}, L(v8,u8)={1,2,3,6,8;4,5,7,8,9}, L(u1,u2,u3,u4)={1,2,7,8,9;5,6,7,8,9;3,4,7,8,10;1,2,5,6,10}。 已知图G=K1*6,2,2,4是完全九部图,那么至少需要9种不同的颜色对图G的各顶点染色。然而,给出的5-列表分配中总共有10种颜色,显然图G的最后一部可以染2种颜色。因为{ν7,u7}部只能选择颜色7,并且{ν8,u8}部只能被颜色8染色,所以最后一部不得不选择颜色9和颜色10,从而图G中其余顶点的染色被依次确定(5-列表分配中标记下划线的颜色)。 3) 下面给出图K1*7,4,6的5-列表分配: {{i,8,9,10,11},i=1,2,…,7, 与情况(2)的分析方法类似,图G=K1*7,4,6的最后两部分别至少需要2种颜色。因为图G共有9部,并且列表分配中总共有11种颜色,那么最后两部中的任意一部都选择2种颜色。首先,最后一部只能选择颜色10和颜色11,接着第8部只能被颜色8和颜色9来着色,最后,前7部不得不依次选择颜色1,2,…,7。因此,通过上述5-列表分配,图G有唯一的列表染色。 4) 给出图K1*7,5,5的5-列表分配如下: {{i,8,9,10,11},i=1,2,…,7, 通过5-列表分配可知,最后2部分必须分别选取2种颜色。一方面,最后一部顶点着色要么选择颜色10和11,要么选择颜色10和8。另一方面,第8部可以用颜色8和9或者颜色8和11来着色。但是,为了从给出的5-列表分配中找到正常染色,最后一部必须使用颜色10和11,而第8部只能选取颜色8和9。因此,图K1*7,5,5中剩余顶点的颜色是一一确定的。 5) 给出图K1*7,2,14的5-列表分配如下: {{i,8,9,10,11},i=1,2,…,7, {1,2,3,4,8;5,6,7,8,9}, 首先,图K1*7,2,14共有9部,且列表中共有11种不同的颜色,那么最后一部的顶点应该用2种或3种颜色来着色。通过分析5-列表分配可知,则最后一部至少需要选取3种颜色,且第8部只能选择1种颜色。已知第8部共有2个顶点,那么只能选择颜色8对该部进行着色。接下来分析最后一部顶点染色情况。在最后一部中先把颜色8排除,此时剩余10种颜色。已知其中有2个顶点的颜色列表为{1,2,3,4,9;5,6,7,8,9},且相同颜色只有颜色9,所以最后一部一定包含颜色9,此时在剩余的颜色中再选择2种颜色即可。通过对顶点颜色进行排列组合,可得到最后一部只能选择颜色9,10,11,其余颜色都不能满足该部顶点正常染色。那么前7部的顶点染色被依次确定。因此,图K1*7,2,14有唯一的5-列表染色。 定理4图G是一个完全k(k≥9)-部图,并且至少有两部顶点数多于1。如果图G不是K1*7,2,r(6≤r<14),K1*7,3,s(6≤s<14),K1*7,4,4和K1*7,4,5,那么图G是U5LC图当且仅当G有一个诱导子图H,其中H是定理3中所研究的U5LC完全多部图之一。 证明:假设图G有一个诱导子图是定理3中所研究的U5LC完全多部图之一,通过引理3可知,图G也是U5LC图。 假设图G不包含定理3中U5LC完全多部图的任意一个作为诱导子图,也不是上面定理中排除掉的少数图,那么证明图G不是U5LC图,即图G具有M(5)性质。下面从两方面对图G进行分析: 1) 图G恰好有2部顶点数大于1。因为G不含有K1*7,4,6,K1*7,5,5,K1*7,2,14作为诱导子图,也不是图K1*7,2,r(6≤r<14),K1*7,3,s(6≤s<14)以及图K1*7,4,4,K1*7,4,5,那么G只能是图K1*7,3,5或者图K1*7,3,5的诱导子图。由定理2知,图K1*7,3,5具有M(5)性质,因此,图G具有M(5)性质。 2) 图G至少有3部顶点数大于1。由于图G不含有K1*5,2*4,K1*6,2,2,4作为诱导子图,那么图G必是K1*6,3,3,3或者图K1*6,3,3,3的诱导子图。由定理1,图K1*6,3,3,3具有M(5)性质,则图G具有M(5)性质。 如图2所示,因受地理位置等因素影响,二级用户A,B,…,J,K间存在干扰关系。以这些二级用户为顶点,干扰关系为边,恰好构成了完全多部图K1*7,2,2。因为主要用户的存在,导致这些二级用户的可用频率并不相同,恰好构成了K1*7,2,2的一个5-列表。由本文的定理4可知,K1*7,2,2具有M(5)性质,那么频率分配方案不是唯一的。这样,当突发因素出现,原有频率分配方案不能实施时,根据M(5)性质,总有其他可用的频率分配方案。 图2 图K1*7,2,2及其列表安排 本文研究了唯一5-列表可染图的特征化问题,除有限个图外,特征化了至少有两部顶点数多于1的U5LC完全k(k≥9)-部图。研究结果表明,在这类图中: 1) 如果图G至少有4部顶点数多于1,那么它一定是U5LC图; 2) 如果图G恰好有3部顶点数多于1,由定理1和定理3可知,图G是U5LC图或图G具有M(5)性质; 3) 如果图G恰好有2部顶点数多于1,若它是定理3中几个完全多部图的父图,则图G为U5LC图,否则图G具有M(5)性质。 本文的结论为完全特征化唯一5-列表可染图奠定了基础,为解决频谱分配相关问题提供了理论依据。对于文中未被证明的有限个图是否为U5LC图,将是未来工作研究的主要内容。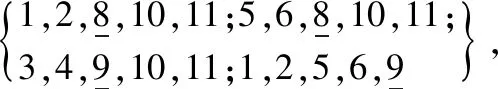

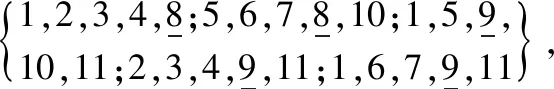
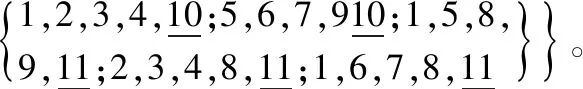
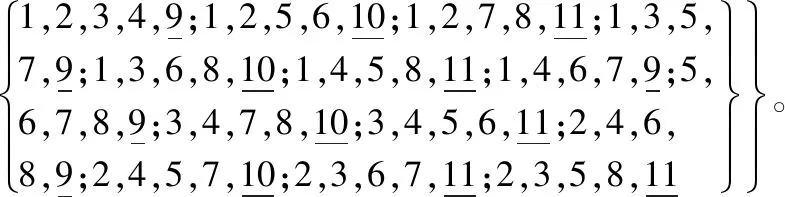
3 应用实例
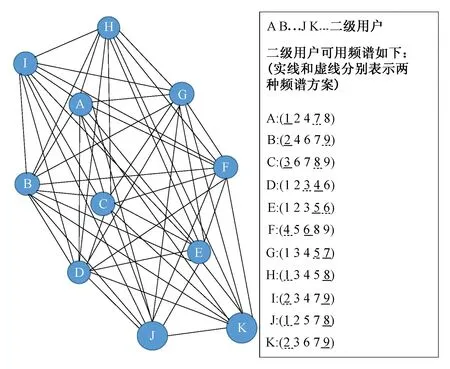
Fig.2 GraphK1*7,2,2and its list assignment4 结论
