低雷诺数透平端部造型控制动叶根部二次流的研究*

2020-07-09段浩杰

风机技术 2020年3期

段浩杰陈榴戴韧

（1.陆军军事交通学院镇江校区；2.上海理工大学能源与动力工程学院）

0 引言

透平内部的损失可分为三类：型面损失、端部损失和泄漏损失。叶栅端区损失在小展弦比透平级的流动损失中占40%～50%的比例[1]。端区的二次流不仅直接影响着流道中的损失结构，而且还影响端壁的冷却保护[2]。因此降低甚至消除叶栅通道内二次流强度，实现对端壁二次流的有效控制变得非常重要。Langston[3]在大折转的高负荷透平叶栅上，通过流动显示，提出了叶栅端区二次流损失的涡流动模型，奠定了叶栅端区流动损失机理研究的理论基础。尽管后续研究更加细致地描述了叶栅端区涡流结构，但是基本构型是一致的，即叶片前缘的马蹄涡在叶栅横向压力梯度的作用下，沿流动扫掠叶栅端壁，形成通道涡后，冲击叶片吸力面端部，造成叶片吸力面角区失速而失去做功能力。

基于Langston二次流模型，提出了若干流动控制方法，如端壁前缘倒角[4]、非轴对称端壁[5]、端壁抽吸[6]，这些方法都得到实验验证。但是在实际透平上应用成功的案例还很少，原因有两个：1）实验多数是在单列叶栅上完成的，与实际透平级条件相差很大；2）叶栅二次流损失与叶栅的负荷分布、叶型以及入口流动参数有很大的关系，还没有一个通用的控制方法。但是这些研究建立了控制叶栅二次流的研究和设计思路，如后加载叶栅的二次损失低于前加载[7]，避免正冲角[8]，采用端弯造型技术匹配动静叶之间的气流角[9]，以及阻止通道涡冲击吸力面扩压段[10-11]等。

低雷诺数是透平设计的另一个重要问题。在低雷诺数下，叶片吸力面流动出现层流向湍流的转捩过程，会出现层流分离，并能再附着，流动损失增加。低雷诺数透平叶型设计偏向采用前加载叶型，但是这种叶型在叶栅端区，导致更大的二次流损失。在文献[10-11]中，通过叶片端区三维造型，控制低雷诺数叶栅的二次流损失。能通过叶片的局部三维造型控制叶栅二次流，对透平叶栅设计有重要价值。

本文选择在一台低雷诺数透平级上，应用负荷控制设计均匀加载叶型，结合前缘倒角思路，对动叶的根部叶型进行局部修改，在级环境中实现对动叶端壁二次流的控制，降低二次流损失。

1 透平级模型

低雷诺数透平模型来自日本AIST的试验轴流单级透平，该透平级是等环量设计，具体几何参数见文献[12]。动叶叶根的原型与改型后的叶型参数如表1所示。新叶根截面叶型采用Pritchard[13]参数法设计，并采用正交试验设计方法优选设计参数，二维叶型的几何型线如图1所示。改型后叶栅喉口尺寸保持不变，以保证通流能力，这时叶型系列面型线在喉口点的斜率是连续的，但是曲率不连续，对透平叶栅，暂时忽略这点不连续对性能的影响[14]。进口气流角设计值与静叶出口气流角相匹配，安装角比原型减小9°，轴向弦长增加8%，Zweifel载荷系数减小1.37%。

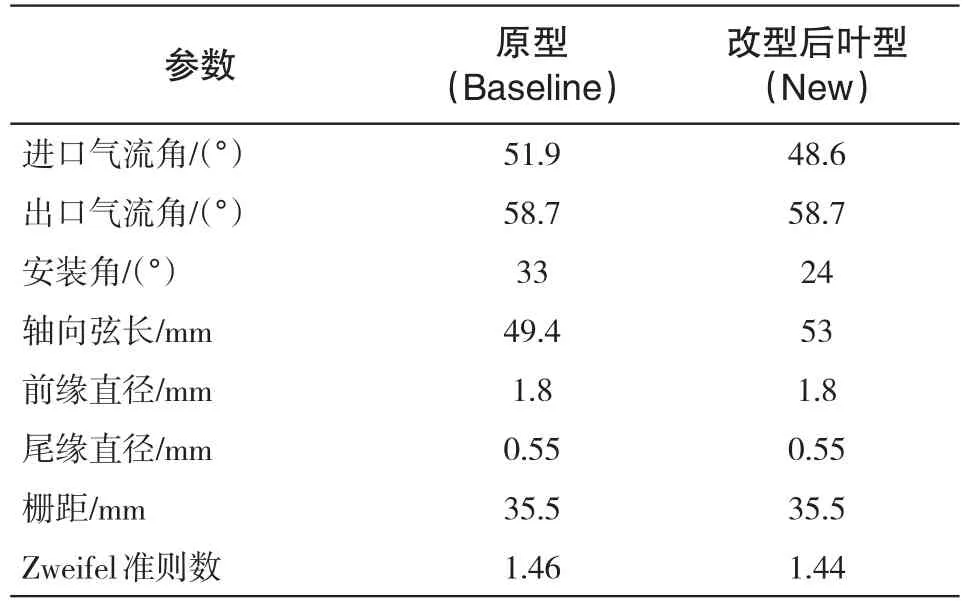
表1 叶栅主要参数Tab.1 Model Turbine Geometric Parameters

图1 叶型几何型线对比Fig.1 The comparison of blade airfoil

应用S1流面流动分析软件MISES[15]，对叶根叶型改进前后的气动性能进行了分析比较。图2～图4分别为叶型表面静压系数、摩阻系数及吸力面边界层厚度分布的对比。相比原型，改型后的叶型吸力面前缘位置均匀加速，到喉口位置扩压，载荷分布呈后加载方式。在40%轴向位置，吸力面的摩阻系数较原型减小。整体而言，叶型的边界层厚度，包括动量厚度和位移厚度都比原型薄。因此，叶栅的总压损失系数也比原型小。

图5（a），（b）为原始动叶与改型后动叶模型对比图，25%叶高截面处叶型与改型后的叶型之间的过渡在端壁处形成了类似前缘壁角(Fillet)的形状，如图5（c）所示，25%叶高到端壁处叶型的过渡，是前缘位置以B样条曲线连接，生成了25%H的前缘壁角高度。

图2 叶型表面压力分布对比Fig.2 The comparison of pressure distribution on the blade surface

图3 叶型摩阻系数分布对比Fig.3 The comparison of friction coefficient

图4 叶型吸力面边界层厚度分布对比Fig.4 The comparison of boundary layer thickness distribution over suction surfaces

图5 改型前后叶片模型对比Fig.5 Baseline and Modified Rotor Blades

2 透平叶栅气动特性分析

采用CFD软件ANSYS-CFX15的定常流动模型计算分析级内流动，假设流动完全是湍流的，采用SST湍流模型作为封闭方程。计算网格采取六面体结构网格，壁面第一层网格高度设为0.01。静叶域网格流向×周向×径向节点数分布为98×46×65，最小角度为31°，最大展弦比311。动叶域网格流向×周向×径向节点数分布为305×70×99，动叶叶顶间隙为1mm，最小角度为24°，最大展弦比197。计算域为静叶前延伸1.5倍静叶轴向弦长，动叶后延伸2.5倍动叶轴向弦长。

透平级实验是在常温常压下开式吸气式风洞上进行的，参考实验条件，数值计算选取工质为常温下空气。进口压力总压为101 456Pa，温度为298K，进口湍流度为0.5%，出口按径向平衡方程给定，壁面设定为绝热壁面，动叶转速为402r/min，动静交界面设定为级间交界面。与实验结果对比，确认了计算网格的无关性，同时验证了模拟计算与实验值趋势基本一致。表2给出原始透平叶栅与改型后叶栅的参数对比，改型后的透平功率比原来增加0.7%，流量几乎没有变化。

表2 透平级主要参数对比Tab.2 Comparison of parameters of the turbine stage

2.1 叶栅端壁流场分析

图6给出原型叶栅与改型叶栅的端壁上极限流线图。从图中可以看出，由于存在负冲角，原型叶栅的端壁处鞍点偏离前缘点位置；而改型后叶栅的进口气流角可以实现零冲角工况，有利于减小端壁处的气动损失。

图6 端壁上极限流线Fig.6 Limiting streamline at the endwall

摩擦系数与壁面附近的速度梯度密切相关，端壁上摩擦系数的演变一定程度上可以反映端区涡系结构的发展。图7给出了端壁上摩擦系数的分布，与原型相比，在x/Cax≤0.5范围内，改型后叶栅通道的摩擦系数整体偏小；靠近前缘处，改型后叶栅的摩擦系数值明显小于原型，这是由于改型后消除了负冲角，前缘鞍点位置发生移动。同时，改型后叶栅无明显的马蹄涡轨迹，说明抑制了马蹄涡的发展，削弱了马蹄涡的强度。

图7 端壁上摩擦系数分布Fig.7 Distribution of friction cofficient at the endwall

本文中，总压损失系数Cpt的定义为：，式中Pt,0表示动叶进口的相对平均总压，Pt表示当地的相对总压，ρ1，V1分别表示动叶进口的平均密度与速度。

为了更清晰的分析改型叶栅对其性能的影响，如图8所示，将径向高度分为三个区域进行分析：端部二次流影响的损失区域（RegionⅠ）、叶中损失区域（RegionⅡ）、叶顶泄漏影响的损失区域（RegionⅢ）。由于本文未考虑叶顶泄漏的影响，图9只给出端区RegionⅠ和叶中位置RegionⅡ沿不同轴向位置平均总压损失值的定量对比。对于RegionⅠ而言，相较于原型，改型叶栅整体的总压损失值较低，尤其靠近前缘处，降低了47.9%。在RegionⅡ区域内，叶根的改型对其叶中的损失变化不大，但在其尾缘处，总压损失值降低了17.7%。

图8 径向高度分区示意图Fig.8 The different region of loss calculation along span

图9 不同轴向位置的平均总压损失Fig.9 Average total pressure Loss Contours at different axial positions

为了进一步研究分析改型对叶栅流场的影响机理,图10给出了叶栅前缘滞止线截面流场流线图以及湍动能云图。对于原叶栅端壁前缘处，由于径向压力梯度的影响，来流边界层形成了前缘马蹄涡，在此位置存在明显的湍动能梯度。改型后叶栅由于减弱了此处的压力梯度，使此处的来流边界层无法形成明显的旋涡结构，进而消除了前缘马蹄涡，此时无明显的湍动能梯度存在。

图10 前缘滞止线截面流场流线及湍动能云图Fig.10 Flow streamline and turbulent kinetic energy at the leading edge stagnation line section for baseline(up)and hub profiled(down)

2.2 叶栅出口流场分析

叶栅出口周向平均总压损失系数沿叶高的分布如图11所示，与原型相比，叶栅出口周向平均总压损失系数的平均值降低了5.4%。由于通道涡的影响，在叶栅出口叶高24%附近出现高损失段，其峰值的大小反映了通道涡的强度。改型后的叶栅，使高损失段的峰值由0.25减小到0.21，减小了16.4%。同时，在叶高15%～50%区段，周向平均相对总压损失均小于原型叶栅。由图12可以看出，在叶高10%附近，过度偏转的气流角减小了2°左右，更趋近于该叶栅的设计出口几何构造角。