电磁轴承水平转子跌落恢复控制策略研究*

赵宇兰 宫海龙 杨国军 时振刚 陈润年 赵 雷

（1.哈电集团中央研究院；2.清华大学 核能与新能源技术研究院）

0 引言

电磁轴承具有无机械接触、微磨损、无需润滑及可主动控制的优点，电磁轴承支承转子动态性能可控、运行精度可控，可实现转子、结构未知特性的辨识。转子系统中应用电磁轴承，可良好地避免转子与轴承之间的机械摩擦、极大减轻磨损与润滑问题[1]，可良好应用于压缩机、鼓风机、储能飞轮等旋转机械系统中，工业应用领域广阔[2-4]。文献[5]基于700kW电磁悬浮鼓风机的实际应用需求，试验研究表明电磁轴承可以满足该鼓风机所要求的工业性能。

转子在空间中的平移以及围绕x轴与y轴的转动均由电磁轴承控制。转子轴向转动由电机控制。为防止电磁轴承失效及发生过载事故引起转子跌落并与电磁轴承碰撞，在电磁轴承系统中加装辅助轴承，为转子提供临时机械辅助支承，并可为跌落转子进行限位。辅助轴承与转子之间的间隙小于电磁轴承与转子间隙，通常为电磁轴承间隙一半[6]。

然而，转子在正常工作状态下仍有受到外界剧烈扰动而失稳，并进一步跌落与辅助轴承发生碰撞的可能。此时，处于工作状态的电磁轴承仍可能具有控制能力。为减轻由非线性碰撞所导致的转子异常动态行为并阻止转子与辅助轴承的进一步剧烈碰撞，控制系统需要具有主动将转子恢复至无接触状态的能力。控制策略要求能够有效减轻碰撞与摩擦，并使转子恢复至无接触悬浮状态。

诸多学者对于转子跌落以及位置恢复问题进行了相关研究。Palazzolo等人研究了摩擦系数、支承阻尼以及单边载荷对于抑制反向涡动的影响[7]，以及转子跌落过程中的温升问题及辅助轴承疲劳寿命[8-9]。Wilkes等人对于转子与辅助轴承的碰撞与相互作用进行了系统分析[10]。当转速低于固有频率时，轴向摩擦将引发同步正向涡动；当转速高于涡动转速频率时，轴向摩擦将引发恒频涡动。

Keogh与Yong[11]指出，转子跌落过程可视为弹跳与摩擦的结合。为阻止柔性转子与辅助轴承接触，文献[12]中提出了一种递归开环自适应控制器，以增加控制器对于波动变化的反应能力。一旦发生碰撞，控制器将及时响应减小碰撞并在无须关闭系统的情况下恢复转子位置。文献[13]表明，同步不平衡力将引发转子进入具有周期性运动与固定碰撞点（旋转坐标系下）特点的稳定碰撞模式。基于以上研究，提出了一种恢复策略可将柔性转子从固定接触碰撞模式恢复到无接触状态。文献[14]与[15]提出了一种具有通过液压传输线与滚动轴承耦合的压电驱动器的主动控制辅助轴承系统，可有效减小碰撞接触力并阻止跌落转子进入连续接触碰撞模式。

文献[16]对于辅助轴承在极限载荷下所承受的轴向以及径向受力情况进行研究。文献[17]在考虑轴向以及径向摩擦力的基础上建立了转子跌落动力学模型，并分析转子旋转频率、刚度以及阻尼对于转子动力学特性的影响。文献[18]建立了转子跌落过程的热学响应分析模型。更进一步，文献[19]在考虑转子围绕x与y轴旋转的基础上，建立转子跌落模型预测竖直转子跌落姿态。文献[20]针对转子跌落实验数据进行分析，评估转子跌落姿态以及转子与辅助轴承的碰撞接触受力情况。

本文通过分析转子振动信号来完成转子位置控制，并在考虑转子接触碰撞的情况下设计电磁轴承PID控制系统。文中的控制策略包含转子跌落碰撞计算模块，数值模拟计算表明该控制策略可将具有跌落趋势甚至已经发生碰撞的转子恢复至无接触悬浮状态，避免碰撞的进一步发生。

然而，跌落转子位置恢复研究目前仍是一个相对开放的问题，仍需后续更为深入的进一步研究。

1 水平转子跌落动力学分析

研究假设转子为刚性转子。转子轴向旋转由电机控制，其余五个自由度均由电磁轴承控制。两对辅助轴承分别布置于转子左、右两端，为转子提供临时辅助支承。当电磁轴承完全失效时，转子将跌落并与辅助轴承发生碰撞。

水平转子跌落动力学模型如图1所示。其中，x，y与z分别表示水平位移，θx与θy分别表示绕x轴与y轴的旋转。a与b分别表示左、右辅助轴承距转子中心的位置。

图1 转子运动简图Fig.1 Schematic of the rotor motion

图2表示转子与辅助轴承的相互作用。C表示转子几何中心，S表示转子质量中心，ρ表示O与C的距离，e为转子偏心距，α为OC与x轴的夹角，α̇为转子涡动转速。θ为转子旋转角度，φ为转子初始相位。转子质心位移与速度可表示为：

图2 转子与辅助轴承相互作用Fig.2 Interaction between the rotor and the auxiliary bearing

转子几何中心位移可计算为：

其中，xa，ya，xb与yb分别为左、右辅助轴承截面处的转子轴心位移。转子绕x轴与y轴的角度为：

其中，左、右辅助轴承截面处的转子轴心位移为：

应用拉格朗日方程分析转子动态特性：

其中，T与V分别表示转子动能以及重力势能；qi表示广义坐标；Qi表示广义力。转子各自由度运动情况可由以下方程表示：

其中，Fxa，Fya，Fxb以及Fyb分别为直角坐标系下转子受力;Fr与Ft分别表示接触力与摩擦力。

辅助轴承中心与转子中心之间的位移可用以评判碰撞是否发生。正嵌入深度表示转子与辅助轴承之间的碰撞已经发生。接触力可由赫兹接触理论计算：

其中，K表示接触刚度；C表示接触阻尼；δ表示嵌入深度；e表示接触系数。

2 跌落转子位置恢复研究

系统正常工作时仍有突然受到外界负载，如突加不平衡、叶片损失或破坏等干扰的可能。此时电磁轴承仍处于工作状态，具有控制全系统的能力。但转子由于受到突然干扰而具有与辅助轴承碰撞接触的可能。为了阻止转子与辅助轴承进一步剧烈碰撞，控制系统需要具有能够主动将具有跌落趋势的转子恢复至无接触稳定悬浮状态的能力。

当转子异常振动时，电磁轴承系统快速响应。此时电磁轴承将对转子施加补偿力，以此减小碰撞或将具有跌落趋势的转子恢复至无接触状态。

转子动态特性可由以下转子动力学方程所描述：

其中，Fxa，Fya，Fxb以及Fyb分别表示转子所受电磁力。

其中，Ks与Ki分别表示位移刚度与电流刚度。

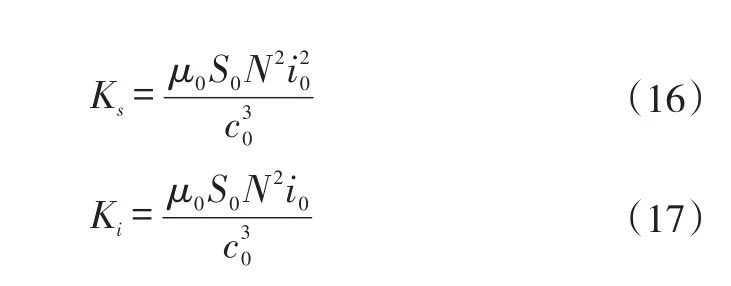
其中，μ0表示真空磁导率，S0为单磁极面积，N为匝数，c0为转子与电磁轴承间隙。

图3对转子某一自由度控制逻辑进行阐述。此模型考虑了转子跌落与辅助轴承发生碰撞的可能。带有预测转子跌落碰撞评估算法的PID反馈控制方法被用于此系统中，用来减少转子对不平衡的敏感度并控制转子稳定运转。

图3 转子某一自由度控制逻辑Fig.3 Block diagram of the control system for one axis

当转子系统受到外界不平衡激励，并由此离开初始稳定位置，控制算法将立即快速响应以阻止转子跌落趋势，并将转子恢复至无接触悬浮状态，并最终避免剧烈碰撞事故的发生。

3 结果与讨论

3.1 转子跌落动态行为预测

转子动态行为预测是转子/电磁轴承系统恢复控制策略研究的先决条件。系统详细参数如表1。

数值模拟中假设转子与辅助轴承摩擦系数为0.15。该细长转子自由跌落过程转子动力学模拟结果如下。

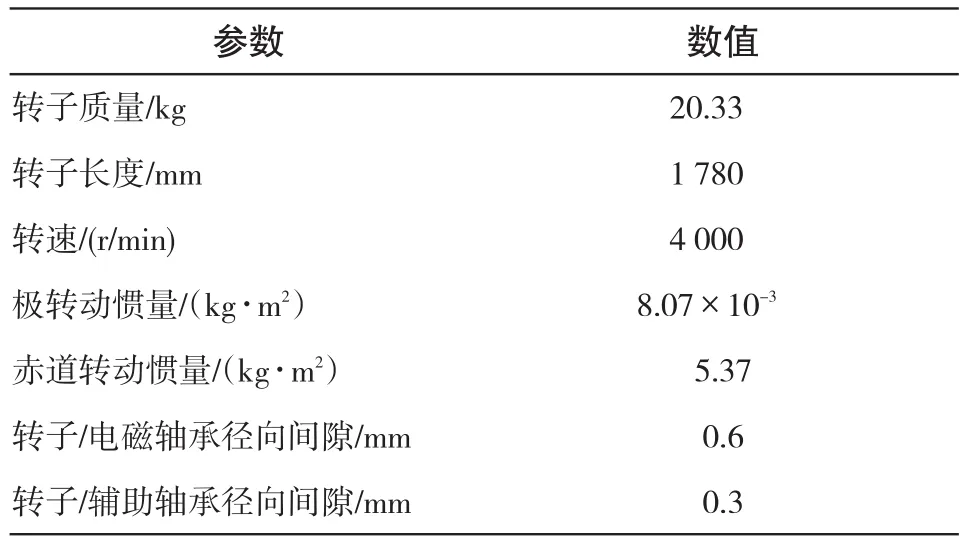
表1 系统参数Tab.1 System parameters

图4与图5分别展示转子左、右截面的轴心轨迹。转子跌落过程中，转子处于连续弹跳以及摩擦的状态。在初始阶段，转子受重力作用而向下跌落。此过程中可观察到转子呈反向涡动状态。在跌落转子与辅助轴承接触之后，转子开始弹跳。摩擦存在于径向碰摩面上。受重力主导影响，全周回转运动较难发展。

图4 左辅助轴承截面转子轴心轨迹Fig.4 Rotor orbit in the cross section of the left auxiliary bearing

图5 右辅助轴承截面转子轴心轨迹Fig.5 Rotor orbit in the cross section of the right auxiliary bearing

预估碰撞力如图6与图7所示。在跌落初期，碰撞较为剧烈，之后逐步衰减直至稳定。碰撞力最终接近重力大小。转子左、右截面处的碰撞力差别不明显。

图6 转子与左辅助轴承碰撞力Fig.6 Left contact force

图7 转子与右辅助轴承碰撞力Fig.7 Right contact force

3.2 转子跌落位置恢复模型有效性评估

对转子施加外界扰动，在第15s时，分别对转子x方向施加持续0.1s的1 000N的力，对转子y方向施加持续0.1s的-1 000N（与重力方向同向）的力。

当不加跌落恢复计算模块时，转子左、右辅助轴承截面处位移分别由图8～图11表示。此时转子发生碰撞，碰撞力如图12与图13所示。此时，转子由于受到冲击而偏离悬浮位置，发生碰撞。首次碰撞冲击受力最大，之后经过几次弹跳逐步衰减。

图8 左辅助轴承截面处转子x方向位移Fig.8 Xdisplacement in the section of the left auxiliary bearing

图9 左辅助轴承截面处转子y方向位移Fig.9 Ydisplacement in the section of the left auxiliary bearing

图10 右辅助轴承截面处转子x方向位移Fig.10 Xdisplacement in the section of the right auxiliary bearing

图11 右辅助轴承截面处转子y方向位移Fig.11 Ydisplacement in the section of the right auxiliary bearing

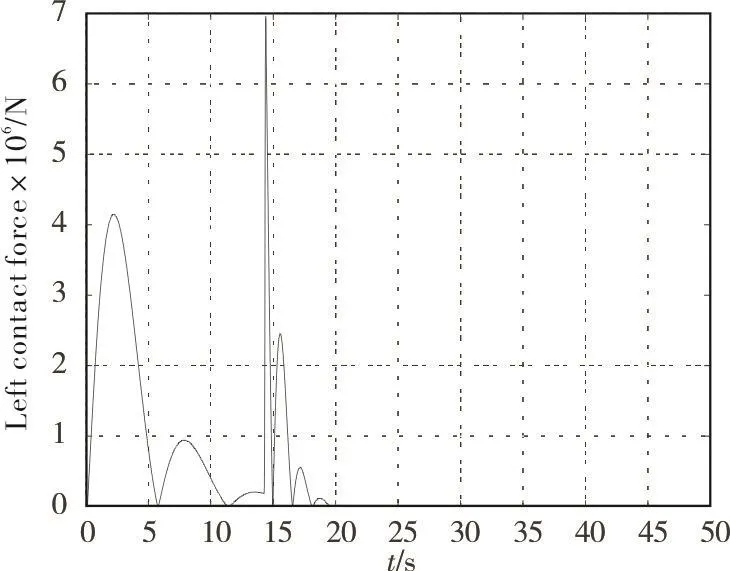
图12 左辅助轴承与转子碰撞力Fig.12 Left contact force

图13 右辅助轴承与转子碰撞力Fig.13 Right contact force

现在控制策略中增加转子跌落计算模块。此时，转子左、右辅助轴承截面处位移分别由图14～图17表示。此时转子仍发生碰撞，其碰撞力如图18～图19所示。

图14 左辅助轴承截面处转子x方向位移Fig.14 Xdisplacement in the section of the left auxiliary bearing

图15 左辅助轴承截面处转子y方向位移Fig15 Ydisplacement in the section of the left auxiliary bearing

图16 右辅助轴承截面处转子x方向位移Fig.16 Xdisplacement in the section of the right auxiliary bearing

图17 右辅助轴承截面处转子y方向位移Fig.17 Ydisplacement in the section of the right auxiliary bearing

图18 左辅助轴承与转子碰撞力Fig.18 Left contact force

图19 右辅助轴承与转子碰撞力Fig.19 Right contact force

在此种情况下，转子仍未能避免跌落并与辅助轴承发生了碰撞。但该控制策略有效减轻了碰撞力的大小以及碰撞发生的持续时间。转子与辅助轴承发生轻微碰撞之后随即便被控制系统重新拉回无接触位置并重新稳定悬浮。该控制策略减轻了碰撞力的大小以及持续时间，减轻碰撞发生的影响。

当转子x以及y方向均受到持续0.1s的400N的扰动时，受转子恢复控制策略影响，转子左、右辅助轴承截面处位移分别由图20～图23表示。此时转子未发生碰撞，碰撞力为0，如图24～图25所示。控制策略可使转子避免受到外界扰动而具有跌落趋势，最终将转子恢复至悬浮无接触状态。

图20 左辅助轴承截面处转子x方向位移Fig.20 Xdisplacement in the section of the left auxiliary bearing

图21 左辅助轴承截面处转子y方向位移Fig.21 Ydisplacement in the section of the left auxiliary bearing

图22 右辅助轴承截面处转子x方向位移Fig.22 Xdisplacement in the section of the right auxiliary bearing

图23 右辅助轴承截面处转子y方向位移Fig.23 Ydisplacement in the section of the right auxiliary bearing

图24 左辅助轴承与转子碰撞力Fig24 Left contact force

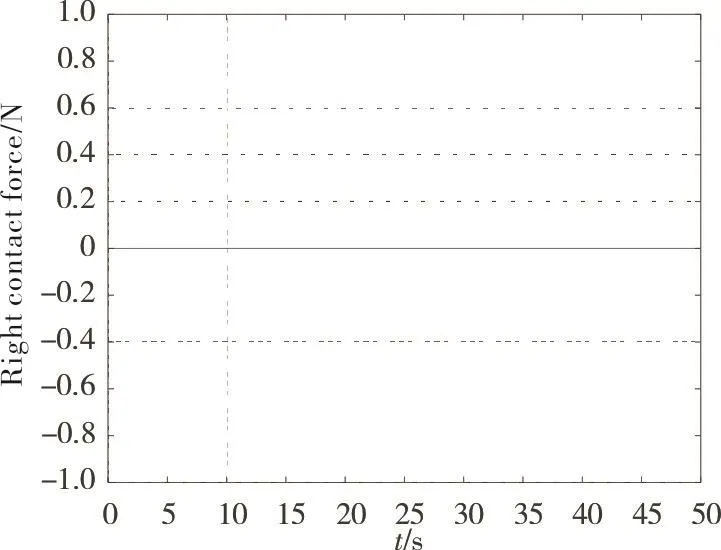
图25 右辅助轴承与转子碰撞力Fig.25 Right contact force

如上，该控制策略可有效减轻甚至避免转子由于外界扰动跌落而与辅助轴承发生碰撞。转子可被重新控制恢复至无接触悬浮状态。

4 结论

本文针对水平细长电磁轴承悬浮转子，进行转子跌落位置恢复控制策略研究。文中提出的包含转子跌落碰撞计算模块的PID控制策略在转子受外界载荷而具有跌落趋势时，可减轻甚至避免转子跌落，减少碰撞力的大小以及持续时间，有效减轻转子跌落带来的影响。