裙座与塔式容器不同连接型式的对比分析
2020-07-09赵菲
赵 菲
(中国石化工程建设有限公司,北京100101)
塔式容器(简称塔器)是石油化工行业重要的单元操作设备【1】.塔器的主要作用是实现气液相或液液相的充分接触,从而达到传质及传热的目的.因此,塔器广泛用于蒸馏、吸收、萃取、洗涤和冷却等重要单元中,其操作的好坏,直接影响着整个装置的质量.
塔器高度和质量都较大,通常需要采用裙座支撑.裙座与塔式容器的连接可采用对接或搭接等型式来实现.对接焊缝必须采用全熔透的连续焊,焊缝的承载能力好;搭接接头为角焊缝,工程中使用较少.标准【2G3】中给出了几种裙座与塔体连接的型式,如图1(a)~图1(c)所示.

图1 裙座与塔式容器的不同连接型式示意
图1所示的结构中,图1(a)是最简单的对接型式.当塔器符合下列情形时,宜采用图1(b)的型式:
1)塔体高度H>30 m,且高径比H/D>15的塔器(D为塔体平均直径);
2)低温操作的塔器或CrGMo钢塔器;
3)裙座与下封头焊缝处可能产生热疲劳的塔器;
4)裙座筒体名义厚度δns≥16 mm的塔器.
对于厚壁容器,根据需要可采用图1(c)所示的有托板的连接型式.使用时,裙座与筒体中径对齐,先将6 mm的托板点焊到裙座筒体和封头上,待托板下部堆焊完成后铲掉托板,再堆焊上部焊缝.
当选用图1(a)和图1(b)的型式时,可根据裙座筒体和下封头的厚度差选用不同的对齐方式:
1)当裙座筒体和下封头的厚度差<8 mm时,裙座宜与塔体内径对齐;
2)当裙座筒体和下封头的厚度差≥8 mm时,裙座宜与塔体外径对齐;
3)当塔体下封头厚度≥60 mm时,裙座宜与塔体中径对齐.
对于中低压的塔式容器,虽然并不是厚壁容器,但在同时承受多种载荷(如内压、重力及弯矩、温度载荷、循环载荷)时,下封头与裙座连接处可能会产生复杂的变形和组合高应力,此时是否也能选用图1(c)的型式呢?
本文针对上述问题,采用有限元方法,主要讨论裙座与塔体的不同连接型式在各种载荷下的强度和刚度的区别,同时考虑了不同对齐方式对连接处的影响.
1 基本参数
以某装置中的1台塔器为例进行讨论,其主要技术参数见表1.
本文利用有限元软件 ANSYS 18.2进行分析研究.根据标准规定的型式,建立3个对比模型.

表1 塔器主要技术参数
A模型:裙座与塔体采用带托板的连接型式,裙座与塔体中径对齐,见图2(a);
B模型:裙座与塔体采用无托板的连接型式,裙座与塔体中径对齐,见图2(b);
C模型:裙座与塔体采用无托板的连接型式,裙座与塔体外径对齐,见图2(c).

图2 裙座与塔体不同连接型式的对比模型示意
本文主要考察裙座与塔体不同连接型式的区别,因此不考虑周边接管等部件.此时塔器是轴对称结构.为提高计算效率,选用轴对称模型进行模拟,利用高阶二维8节点单元,计算模型中厚度扣除腐蚀裕量.
需要说明的是,椭圆形封头建模采用JB 4732—1995(2005年确认)第7.6.3节公式计算部分的标准椭圆封头,即采用球壳和过渡段环壳两圆相切的结构(以下简称两圆相切处),球壳内半径Ri=0.9Di=2 340 mm,过渡段环壳内半径r=0.17Di=442 mm,3个对比模型的有限元模型示意见图3(a)~图3(c).模型的材料性能数据见表2.
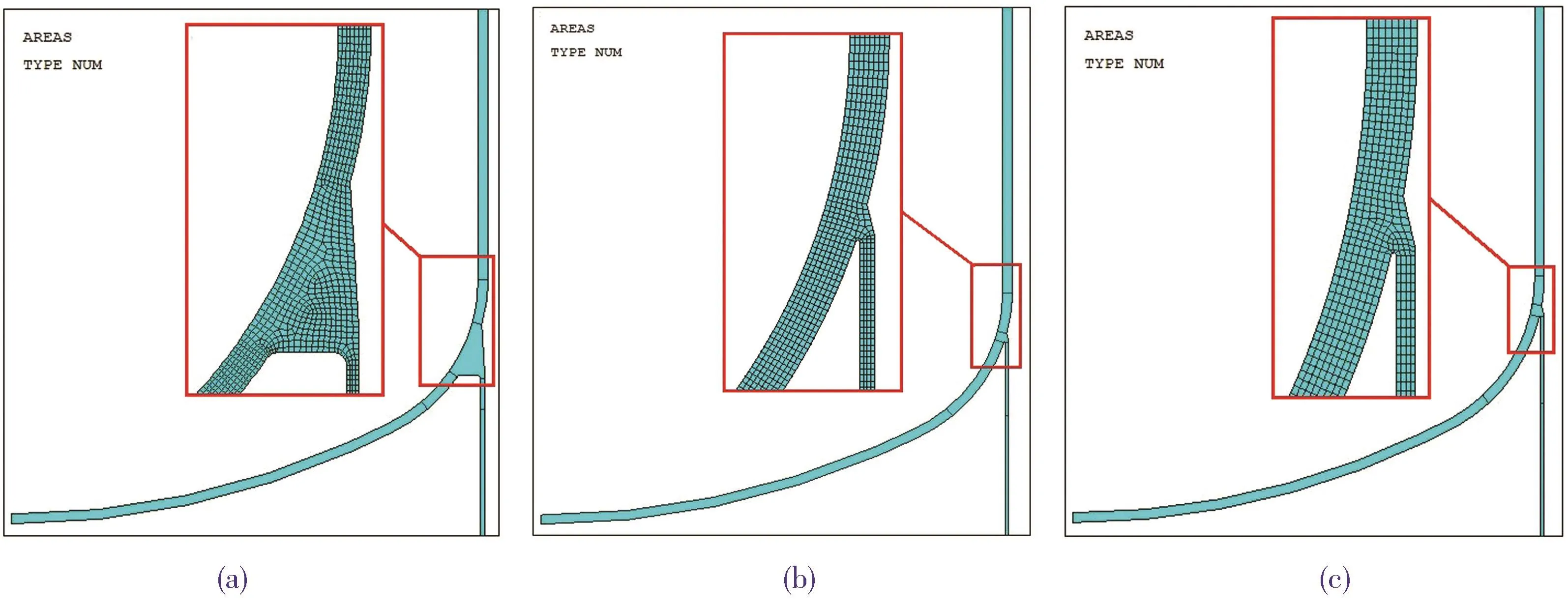
图3 对比模型的有限元模型示意

表2 材料性能数据
对3个模型分别施加内压、重力、温度载荷,对比各个模型在相同载荷下的变形和应力分布.
2 内压计算
对各模型施加内压进行计算,A模型的位移分布云图见图4.
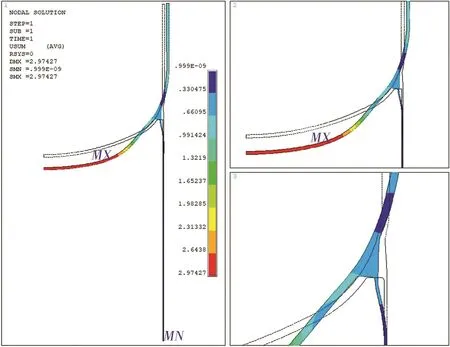
图4 内压载荷下A模型的位移分布云图(50×)
由图4可以看出:A模型在内压的作用下,筒体径向膨胀,椭圆形封头发生“趋圆”现象,连接处由于焊缝填充金属较多,截面大、刚度大,与附近壳体的变形产生较大差异,因变形协调而导致封头上两圆相切处产生较大应力.B模型与C模型的位移趋势和应力最大点位置与A模型相似.
在连接处周围取路径1-1′~3-3′,过应力最大点取路径4-4′进行对比,3个模型的应力分布及路径示意如图5(a)~图5(c)所示,具体数值见表3.由表3可以看出:由于A模型比其他模型连接处的截面更大,强度和刚度更大,所以在内压载荷作用下的最大总应力值最低,变形最小,路径4-4′上的值也最小;B模型与C模型的最大总应力值相差不大.
在连接处周围的路径中,由于C模型的焊缝位置更靠近封头边缘,此处封头在内压作用下产生的经向应力和周向应力都小于A、B模型,因此各路径的值明显小于其他模型.A模型的1-1′和3-3′两条路径数值都小于B模型,但对于2-2′路径,A模型在此处因变形协调产生的局部应力大于B模型.
3 重力载荷计算
对于本文研究的塔式容器,还需要核算连接结构在重力和外力矩作用下的强度.由于重力和外力矩在连接处产生的是沿裙座轴向的应力,因此本文只在模型筒体的顶截面施加竖直向下的等效重力载荷100 t(包括设备金属重、介质总重、外力矩的等效力).计算出的应力分布云图见 图6(a)~图6(c),具体数值见表4.

图5 内压载荷作用下3个模型的应力分布云图及路径示意
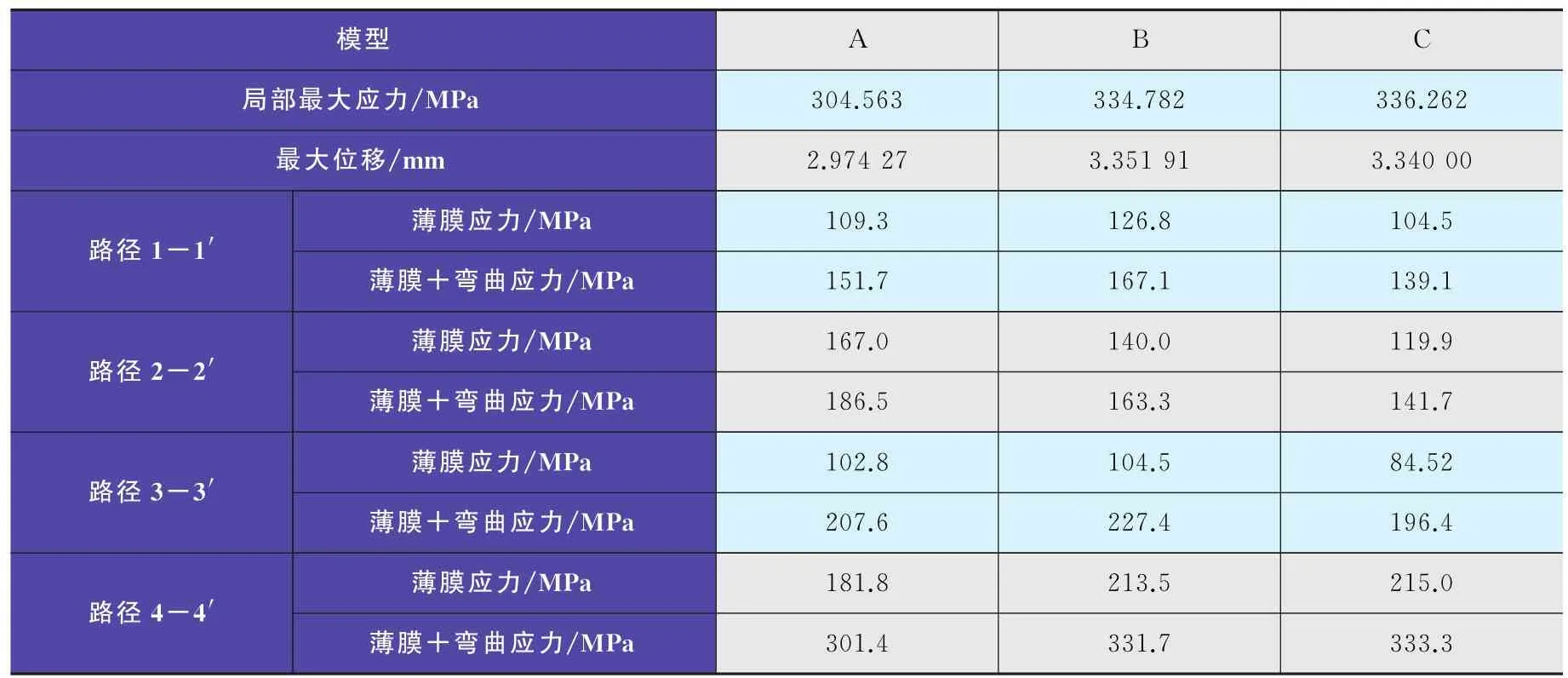
表3 内压载荷作用下3个模型的应力数值

图6 重力载荷作用下3个模型的变形(500×)及应力分布云图
由图6和表4可以发现:在重力载荷的作用下,各模型的位移最大值相差不大.A、B模型的变形趋势相似,最大总应力出现的位置都在连接处焊缝底面与裙座内表面的交点.由于C模型是外径对齐,重力载荷在裙座顶截面会产生一个附加弯矩,使裙座顶面向设备内弯曲变形,因此最大总应力出现在连接处焊缝底面与下封头外表面的交点.A模型连接处的截面最大,总应力值最小;B模型和C模型的总应力值相差不大.
对于本文研究的设备,重力载荷产生的应力值远小于内压载荷作用下的应力值,连接处周围的路径应力值相差不大,此处不再罗列数据进行比较.
4 温度场分析
该塔器工作温度为150℃,最冷月平均温度-16.3℃,操作工况下,裙座与塔体连接处存在温度梯度,会产生热应力,需要进行温度场分析.各模型的温度分布见图7,应力分布云图见图8,具体数值见表5.

表4 重力载荷作用下3个模型的应力数值
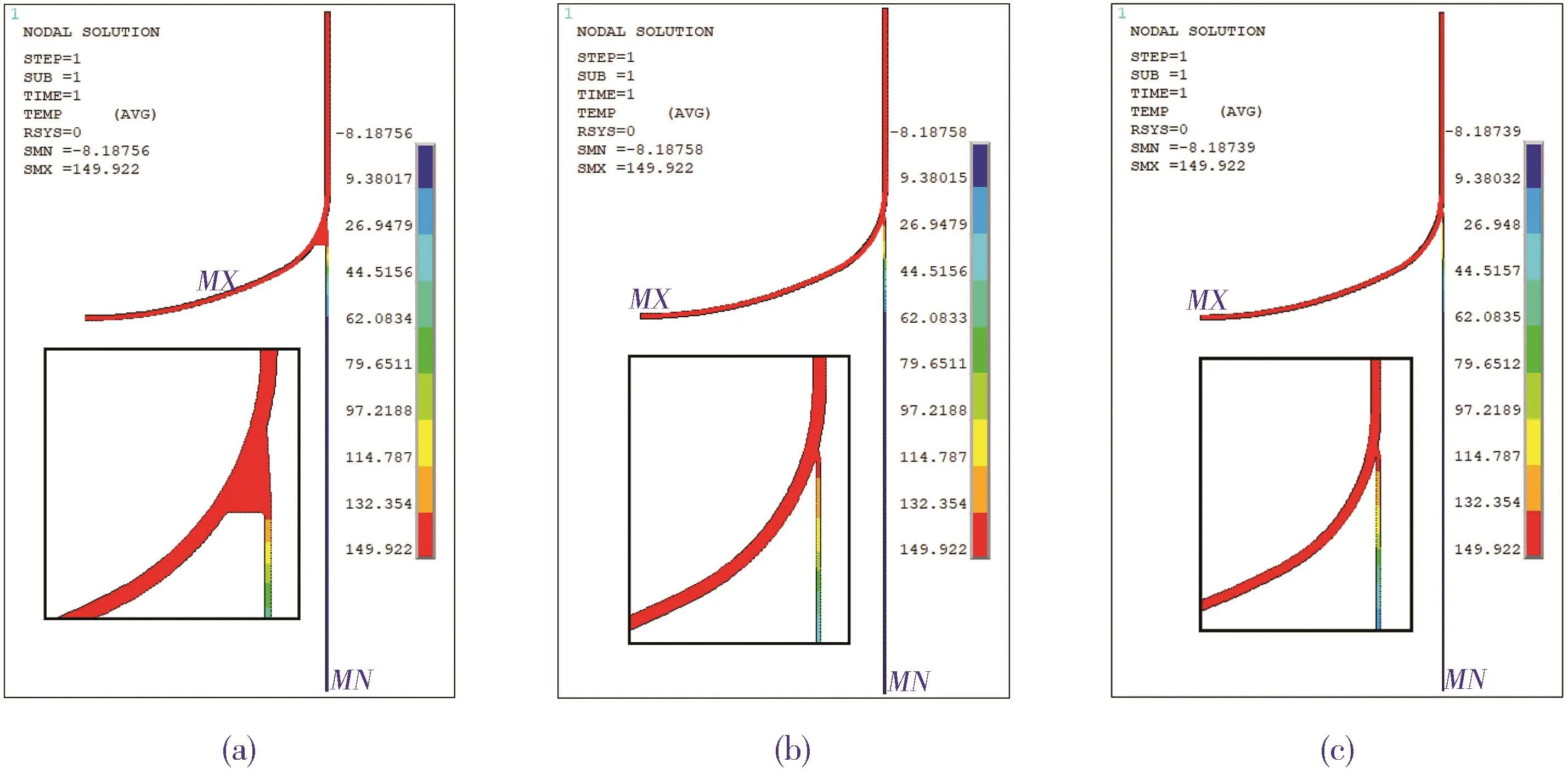
图7 3个模型的温度分布云图

图8 温度载荷作用下3个模型的应力分布云图
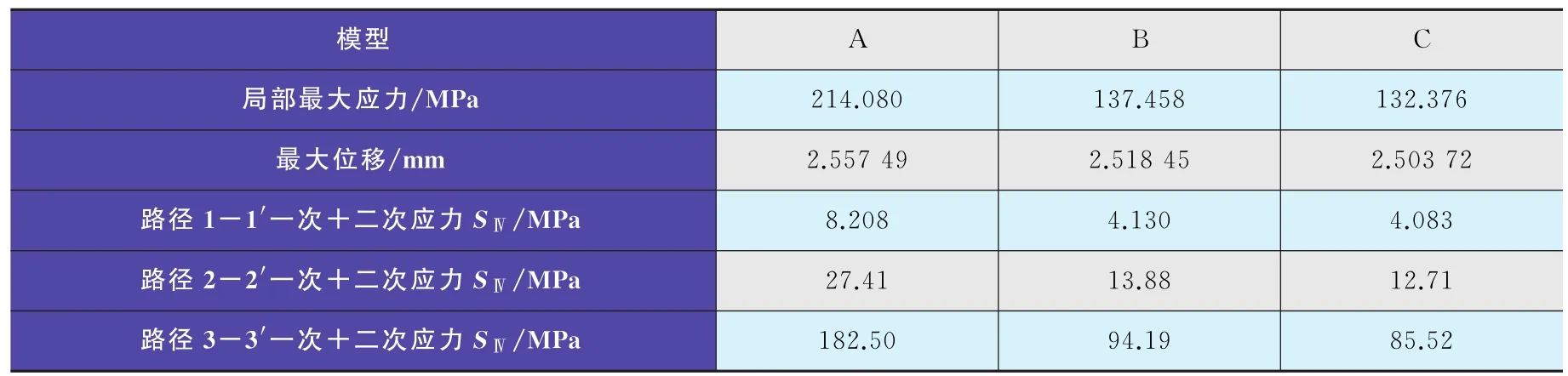
表5 3个模型的热应力数值
计算结果显示,3个模型的应力最大点都出现在连接处焊缝底面与下封头外表面的交点.A模型连接处截面大,当下封头受热膨胀时,对连接处周边的约束也较大,所以产生的热应力也远大于其他两个模型.C模型的热应力略小于B模型.
5 疲劳分析
按照本塔器的工艺条件(即工作内压0.03~2.15 MPa、重力载荷100 t、介质工作温度150℃),计算各模型在工作载荷下的循环次数,其应力分布云图见图9,具体数值见表6.
由图9可以看出:3个模型的应力最大点位置与内压载荷作用下的位置相似,都出现在封头内表面,说明在这3种载荷中,内压载荷引起的应力占了主要成分;各模型的变形与应力值差别也与内压载荷作用时相似.
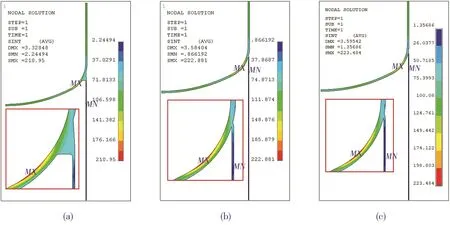
图9 工作内压、重力和温度载荷共同作用下3个模型的应力分布云图

表6 工作内压、重力和温度载荷下3个模型的应力数值
该塔器的总工作循环次数是1.5×105次,忽略开、停工工况和水压试验工况的循环.对3个模型进行疲劳计算,计算过程见表7.
按照标准的要求进行评估,3个模型都可以满足疲劳工况的要求.由于此工况中内压占主要成分,所以选用有托板连接结构的A模型更好,同样,对于无托板的连接型式,B模型与C模型差别不大.

表7 疲劳载荷作用下3个模型的计算过程
6 结论
对裙座与塔式容器的不同连接型式进行了对比分析,并考察了不同对齐方式在各种载荷下的区别.所得结论如下:
1)有托板连接结构的连接处截面大,强度和刚度好,在内压和重力等机械载荷作用下的受力情况较好,但在温度载荷的作用下,热应力比无托板的连接型式更大;
2)无托板的连接结构简单,施工方便,焊接工作量较小,在塔器介质温度较高,尤其是热应力占主要成分(如低压高温塔器)时,宜选用无托板的连接结构;
3)若选用无托板的连接结构,外径对齐的方式在连接区域产生的热应力较低;
4)无托板的连接结构在重力载荷作用下,中径对齐比外径对齐的方式连接区域的受力更好.
在实际工程中,有托板连接结构工序复杂,焊接量大,但可以保证焊缝尺寸,且焊接质量更好.无托板连接结构由于裙座内表面与封头间隙太小,无法打磨,焊态很难保证圆滑过渡.设计裙座与塔体的连接型式时,不仅要考虑本文的分析结论,还要结合塔器的大小、载荷工况、制造难度、成本等因素综合考虑.
