基于光变曲线的典型空间碎片旋转轴指向分析

李同 郑永超 赵思思 尚卫东 张景豪

（1 北京空间机电研究所，北京 100094）（2 中国空间技术研究院空间激光信息感知技术核心专业实验室，北京 100094）

0 引言

近年来国内外航天发射活动逐年增多，而目前在轨有效运转的航天器只占了发射总量的一小部分[1]，其他的航天器因运行寿命和利用消耗等原因，碰撞、解体产生了大量空间碎片，尤其在近地轨道（LEO）上。空间碎片的运行导致与在轨航天器发生超高速撞击，产生的压强远大于表面材料的承压上限[2]，对航天器的正常运行及航天员的安全返回造成巨大威胁[3]。空间撞击事件频繁发生，尤其是2009年美国铱星33 与俄罗斯2251 号卫星发生的碰撞更是敲响了空间环境清理的警钟[4-5]。据美国空间监视网（SSN）统计，近年来空间碎片数量逐年加速增长，且碎片的形状与材料分布多样[8]，严重威胁到航天活动的安全及持续发展[6-7]，因此，对于空间碎片主动清除技术（ADR）的研究迫在眉睫。

诸多寻求可行清除技术的研究与计划在国外已陆续开展，如ORION 计划、ROGER 计划、e.deorbit 计划等；国内也已将相关研究提上了日程[9-10]，对于不同尺度碎片的清除提出了不同方案[11-13]。空间碎片的形状结构多样，尤其是微小碎片更加难以区分及跟踪，目前主要的清除方案如绳系法、抓捕法等都必须获得目标的旋转参数信息。旋转参数包括旋转周期和旋转轴指向，对它们的提取及分析，可对进一步确定碎片空间姿态、精确定轨以至实时追踪等过程给予参考和帮助。

碎片自身的旋转会导致观测光度信息和测距残差产生周期性变化，因此对碎片目标进行光度和测距残差变化分析是提取旋转周期和旋转轴指向的有效手段。国内外对于旋转周期提取方面的研究已较为成熟，而目前的旋转轴指向提取方法多是实测获取光变或测距信息，与假定旋转态下模拟的理论光变或测距数值进行匹配来确定。早在1979年，Williams[14-15]就提出了利用同一旋转周期内的光度差异来确定柱形火箭旋转轴指向的思想；2006年，Charles Wetterer 等[16]通过分析空间目标基于时间序列的光度曲线的周期性变化情况，成功区分出了卫星、火箭箭体和碎片；2012年，Cowardin 等[17]对火箭体碎片旋转状态和翻转率进行了研究，以获取数据支撑其主动空间碎片清除项目；2013年，Santoni 等[18]利用光度差值与旋转角度的相关性对SL-12 火箭体的实测数据进行处理，解算了旋转轴指向；2016年，Kucharski 等[19]通过寻找激光指向两个相邻角反射器的中间位置来确定目标的旋转轴指向；2019年，刘通等[20]提出了基于漫反射激光测距数据估算火箭残骸翻滚姿态的方法，推算Soyuz 残骸的旋转轴向。这些研究大都需要假定足够多的目标先验信息如物理模型、角反射器相关位置参数等，且利计算的光变或测距数值遍历匹配的过程比较复杂。

目前多数通过光变分析提取旋转轴指向的研究都集中在柱状空间目标上，而根据地面卫星超高速撞击解体实验获得的碎片形状统计显示，片状、块状碎片占比较大[21]。因此，本文综合考虑碎片运动、材料、外形结构等各方面特性在目标旋转参数变化下对光度信息产生的影响，提出了一种碎片运动下的光度探测仿真平台搭建方案，基于该平台进行了典型方体碎片旋转运动光度探测仿真，分析了该类碎片光变峰谷间光度差值随旋转轴相位角的变化规律，并通过光变分析近场模拟试验加以验证，进而利用该规律推算光源与接收装置间相对位置变化下可缩小的旋转轴指向存在区间，达到简化旋转轴指向遍历赤经、赤纬取值的流程，提高旋转轴参数提取效率。

1 目标光度探测仿真平台

1.1 目标探测模型

空间目标光度作为一类重要且较为容易获取的空间目标特性数据，可以提供丰富的光学信息，有效反映目标的光散射特性，既是空间目标识别的重要依据，也是空间目标特性分析的重要手段。本文中分析的目标光度是指探测器接收到模拟碎片目标散射的光通量总和，目标光变是指在碎片目标运动过程中同一周期内的光度变化趋势。因此，仿真中需尽可能考虑目标运动过程中影响光度探测的目标特性，如目标的轨道特征、运动特征、结构特征、材料特征、背景辐射特征等。对于碎片而言，其旋转状态复杂，因此需要根据不同的碎片目标特性搭建合适的仿真平台，尤其是目标材料和结构特性各不相同导致获得光变信息的不同。综合考虑上述因素，本文提出了一种空间碎片运动光度探测仿真平台的搭建思路（如图1 所示），对目标面元分割获取结构模型，对双向反射分布函数、光散射截面分析获取材料与反射模型，对目标运动姿态分析获取相对运动模型，最终得到目标整体的光度探测模型。

图1 空间碎片旋转运动光变探测仿真平台搭建流程Fig.1 A construction process of the space debris rotation optical variable detection simulation platform

对于目标结构，通常选取碎片可简化的典型形状进行研究，基于典型形状所表现的各自几何特征来表征结构特征对目标光度信息变化的影响。对于球体及类球体碎片来说，各向同性反射条件下，其光度变化并不明显，考虑光变的复杂性以及典型形状的适用性，本文以方体碎片为例进行光变分析。仿真中需要计算目标投射到探测器像面的光通量，需对目标表面作面元分割，此时面元线度与探测器参数之间需满足：

式中a1为面元划分量级；L表示探测器和碎片间距离；f为探测器焦距；μ为探测器像元线度。实际分割过程中，在确定尺度时需考虑划分尺度与运算效率间的平衡关系。确定了划分量级后，面元位置可由面元几何中心坐标代替，后续对于整个目标结构的分析也就解算成对于所有面元变化情况集合的分析。

1.2 表面光学散射特性模型

空间碎片本身不会自我发光，因此观测中得到的反射光谱主要是碎片表面特性和太阳光谱共同作用的结果，一般用光谱反射率或者反射亮度系数来表示碎片本身反射太阳光的能力，光谱反射率与反射光的波长有关[22]。在考虑入射光光谱辐照度时，参照太阳光在多谱段的光谱辐照度曲线，测得探测器接收可见光内光谱范围λ1～λ2时入射光辐照度E(θi,φi,λ)为：

式中Ek为光谱范围内任一波长λk的入射光谱辐照度；分别为入射光和散射光的天顶角。对于碎片而言，由于其非合作运动及太阳光源、碎片目标和探测装置间的收发夹角（下文通称收发夹角）的变化，导致观测到的碎片截面是不断变化的，因此可利用双向反射分布函数（BRDF）来分析碎片因方位角的不同而显现的反射光谱特征的变化。BRDF 描述了目标某一方向上的入射光线经目标反射后，反射光在目标表面的反射和散射特性，其数学描述为出射指向kr的辐射亮度和入射指向ki照射到单一面元dA上的辐照度之间的比值[23]，即

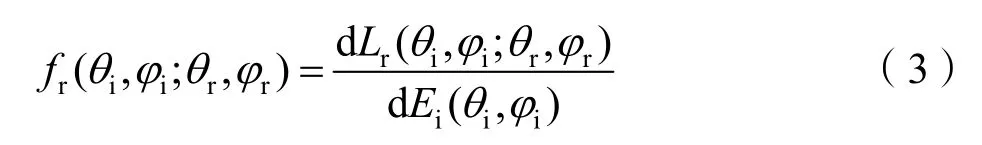
式中θi和φi分别为入射光线的天顶角和方位角；θr和φr分别为出射光的天顶角和方位角；辐射亮度dLr定义为辐射方向上单位面积内的辐射通量；为确定材料特性下的BRDF 值。根据面元划分量级，均匀分割后的任意单一面元dA的几何关系如图2 所示。

考虑模拟碎片目标的材料特性和表面粗糙度，建模中使用了文献[24]中提出的可较好拟合金属粗糙表面的BRDF 模型，其拟合表达式为

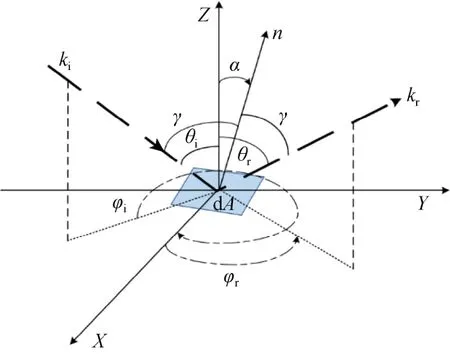
图2 单一面元表面散射关系Fig.2 Scattering relationship for a single surface element

式中kb，kz，b，a，kd为待定参数；G(θi,θr,φ)为表面遮蔽函数；α为法线的倾斜角；γ为微元的光反射夹角；φ为相对方位角。

目标的光散射特性通常用光学散射截面OCS 表征，即

式中A为有效散射面积。此时被测面元经过探测器光学系统反射到像面的光通量φk为

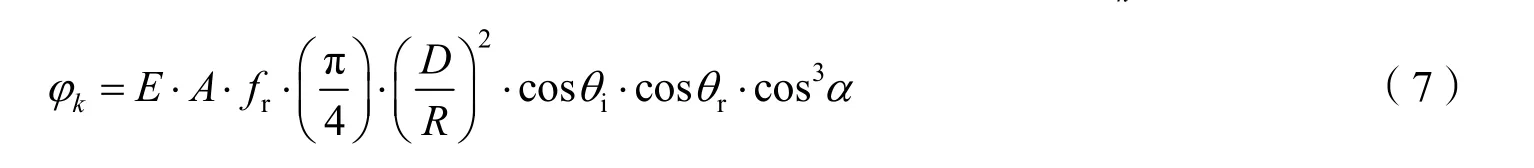
式中E为面元接收到的太阳散射光辐照度；D为探测器入瞳直径；R为被测面元在光轴上的投影与探测器光学系统间距。设光学系统透过率为τ，考虑深空背景辐射影响，则探测器接收到的碎片目标总光通量φ为探测器所有可视面元反射传递的光通量之和：

式中M为黑体背景的辐射出射度；fr,k为第k个面元的BRDF 值；m为面元划分数量。目标单一面元的光度探测原理如图3 所示。

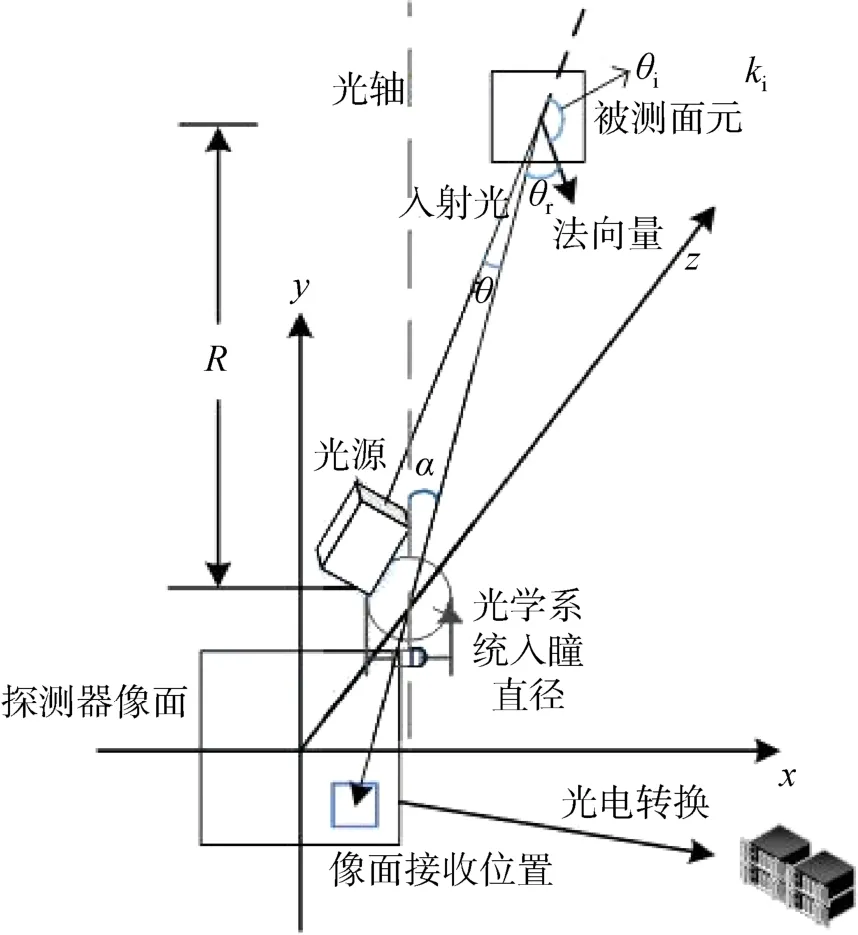
图3 碎片目标被测面元光度探测计算模型Fig.3 The light curve calculation model of a space debris measured surface element

2 典型碎片光度变化分析

2.1 目标光变探测仿真

影响目标光度信号变化的因素主要有观测中瞬时旋转态的变化以及相应旋转状态变化导致的目标光散射特性的变化，仿真中应根据这些影响因素考虑具体参数及条件设置。考虑到模拟目标的典型结构及空间碎片尺度，设置仿真中的方体目标三边长度均不相同，分别为0.7、0.4、0.2m，探测器参数选择焦距f=500mm，像元线度μ=15μm，综合考虑划分量级和运算效率间关系，选择面元划分量级a1=0.1m，每个面元的瞬时BRDF 值由五参数模型计算得出，取决于设置目标的具体材料特性，因此需要选择典型空间碎片材料进行模拟。

通过对典型类碎片目标来源与成分的分析，可选择航天器表面黄色包覆材料作为典型材料建立反射特性模型。本文参照文献[25]，以该类材料为例进行反射特性测量试验，从而计算获得卫星表面包覆材料BRDF 统计模型参数，对该类材料包覆下的碎片模型进行反射特性分布建模，构建目标散射天顶角、反射天顶角、瞬时旋转态与BRDF 参数间的关系。考虑实际空间观测条件下难以做到全时段观测，仿真中在同一周期内反复抓取瞬时时态光度信息，对所有瞬时光度进行拟合获取光变曲线，其中旋转姿态的变化和探测方向的遮挡失光是影响瞬时光度信息的主要因素，具体如图4 所示。假定目标密度均匀，以重心为原点O，以探测方向负向为x轴正向，以初始旋转轴指向为z轴正向，以垂直于x、z轴的任意指向为y轴正向，作旋转态参考坐标系如图4（a），旋转轴绕x轴转动方向定为横向，绕y轴转动定为纵向，探测方向同旋转轴间夹角为P角。考虑旋转轴指向的可取值范围，使得任一旋转轴在该坐标系中均以纵横向取-90°～90°定义，遍历各纵横角确定的旋转状态，观测得出每个轴向内完整周期光变曲线。

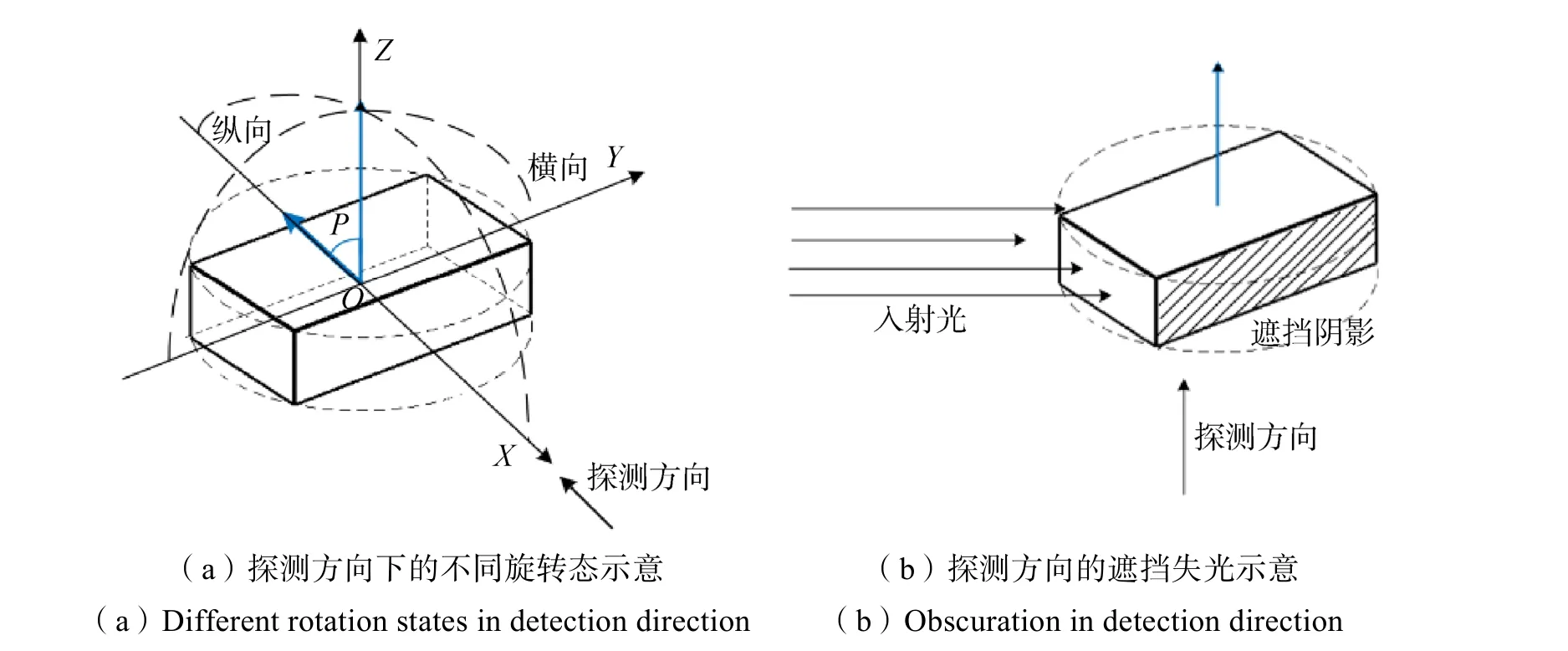
图4 影响瞬时光度信息的因素Fig.4 Factors affecting instantaneous photometric information

另一个影响瞬时光度的因素是目标旋转过程中，可能因入射光同探测方向之间存在收发夹角导致的探测方向的遮挡失光现象，如图4（b）。此时需要对遮光现象作判定，判断入射光实时照亮的所有面元是否都在探测方向的视场内出现，或者判断探测方向可视的所有面元是否都可被入射光照射，继而确定瞬时状态下实际的光回波总辐照度，观测此类状态下的光变情况。设入射光与探测器的接收位置间的初步相对角度为1γ，定义理想收发状态下近似γ1=0 ，此时遮挡失光影响降到最低，且入射光天顶角iθ同反射光天顶角rθ间满足

在理想收发状态下统计观测光变，经分析得到在保持纵向取值不变，即夹角P稳定不变时，旋转轴绕不同横向取值，取向即存在于以碎片目标质心为顶点、观测方向为轴、P为顶角的锥面上，以P角的两个不同取值α和β为顶角形成的旋转轴锥面如图5（b）所示。对此时不同锥面上的旋转状态进行一段时间观测，得到的该时间区间内光变极大峰值与光变极小波谷的变化趋势及峰谷间差值变化如图5，其中，每个完整观测的周期内光变极大值与极小值的变化不单一，在0°～10°以及80°～90°区间内因部分镜面反射光通量进入视场而对漫反射光度产生影响导致峰谷值变化。但光通量峰谷差值存在单一变化，在P处于0°～70°的区间内时，观测方向接收的光通量差值由0 逐渐增大，70°～80°区间由于增大速度减缓接近稳定，80°～90°区间开始明显增大。

图5 探测方向与旋转轴间夹角P 变化下的光度变化Fig.5 Photometric change curves under P change

而对于同一锥面内的不同方位旋转轴，即纵向取值不变，P角固定下的不同旋转轴形成的旋转状态而言，以P=30°为例，对以该角为顶角的同一锥面上不同方位旋转轴形成的旋转态作一段时间观测，得到的该段时间内峰谷间差值变化（如图6 所示），此时的差值变化趋于稳定，上下浮动低于0.5%。考虑观测过程中可能存在误差，探测方向与旋转轴间夹角固定时，不同方位旋转轴间的光变峰谷差值趋于稳定，综合上文可得出如下结论：在接近理想接收发射状态（即收发角度接近0°时），观测未知碎片目标完整周期内的光变峰谷差值，即可确定此时旋转轴同探测方向间夹角缩小在一个极小范围内，进而确定旋转轴可能存在的一个或多个以该夹角为顶角形成的锥面。为验证该结论，下文进行了目标光变差值分析试验，以观测目标不同旋转轴向的成像变化，并分析其光变差值的变化规律。

图6 探测方向与旋转轴间夹角（P 角）稳定下不同方位旋转轴全周期内光变差值Fig.6 Light curve deterioration of the rotation axis in different directions without changing the angle P

2.2 目标光变差值分析试验

试验选取的目标表面材料为典型碎片材料黄色复材包覆薄膜，方体碎片三边分别为0.03、0.03、0.01m。搭建目标旋转运动平台，试验中使用大恒MER-131-210U3M 探测器，像面接收位置与被测目标间距离2m，光源与接收装置间的收发夹角为10°；目标固定在转台，通过移动转台方位来改变旋转轴方位，设定目标在转台中央绕轴匀速旋转，观测不同旋转轴下一个完整周期内的目标成像变化。

图7 是探测方向与旋转轴之间不同夹角时的目标单一周期内成像变化，图中每一排为固定角度同一周期内不同时刻的瞬时观测图像，在不同旋转态下的同一完整周期内目标在像面成像的光度峰值和谷值均不相同。对所有成像数据进行比对，取图像灰度值作为目标瞬时光度值，计算同一夹角下的目标光变差值，进而得到P角变化下的光变趋势。

统计每幅图像灰度值作为瞬时光度值来计算目标光变，反复抓取瞬时光度信息，拟合获得一个完整观测周期内目标光度极值随观测方向与旋转轴间夹角变化趋势（如图8 所示）。同一周期内的光变极值随着P角的变化而改变，光变极大值先减小后增大，极小值随着P角的增大而减小并趋于稳定，光变差值随轴相位角的增大而增大。该试验结果验证了仿真平台的模拟结论，但也因实际观测条件存在难以忽略的误差导致变化趋势存在波动，尤其是光源与接收装置间的收发夹角难以趋近0°所造成的影响。

图7 不同旋转态目标同一周期内成像变化Fig.7 Imaging changes of targets in different rotation states

图8 同一观测周期下探测方向随旋转轴间夹角P 变化的观测光变曲线Fig.8 The light curve of the detection direction with the change of P angle under the same observation period

3 基于光变的目标旋转轴向提取分析

由于实际观测情况下难以忽略由于收发夹角的存在导致光传递遮挡，进而导致观测光度产生误差等影响，因此本节基于光度分析模型对不同收发夹角下的光度变化进行仿真。仿真中取收发角度为5°，其余参数如2.1 中所设，建立目标反射特性模型及相对运动模型，进行目标光变探测仿真。考虑到误差对差值增幅较小的区域产生的影响更为明显，因此以2.2 中的结论为参考，取差值增幅平缓的0°～60°区间进行仿真。

在固定收发夹角下分别取旋转轴相位角即P角为10°、20°、30°、45°、60°，得到每个顶角确定的旋转锥面，遍历求得每个锥面上不同方位旋转轴所确定的旋转状态下的光变差值，上述角度下光度差波动值域如图9 所示。每个P角所确定的旋转轴锥面上的不同方位旋转轴，其对应的不同旋转状态下的完整周期光度差值不再如图6 稳定，存在一个较为明显的光度差波动值域。当未知旋转态目标的测量光度差值位于某个P角所确定的值域内，即存在该目标的旋转轴与观测方向间夹角为P的可能；反之，若该目标的测量光度差值不在该值域内，则可排除相应夹角为P的可能性。此时获取未知目标光变曲线进行处理分析后得到其光变差值，与该类目标差值波动值域进行比较，确定值域上限及值域下限对应的旋转轴向与探测方位间夹角区间，即为旋转轴向可能存在的区间。

图9 不同旋转轴相位角下的光变差波动值域Fig.9 Ranges of light curve fluctuations on different rotation axis phase angles

在上述条件下取遍历光度差值的取值进行反演，确定其值域上下限所对应的P角取值区间（如图10所示），可知在目标不同光度差值取值下，其P角可能存在的最大值域区间不超过8°，与理想收发状态下的该光度差值对应P角取值kα比较，对应的P角取值区间即为kα±4°。每个确定的P角取值决定了一个锥面上的360°不同方位旋转轴取值，因此缩小旋转轴与探测方向间夹角的可取值区间，即使得遍历寻找目标旋转轴向的取值范围由360°×90°缩小为360°×8°。

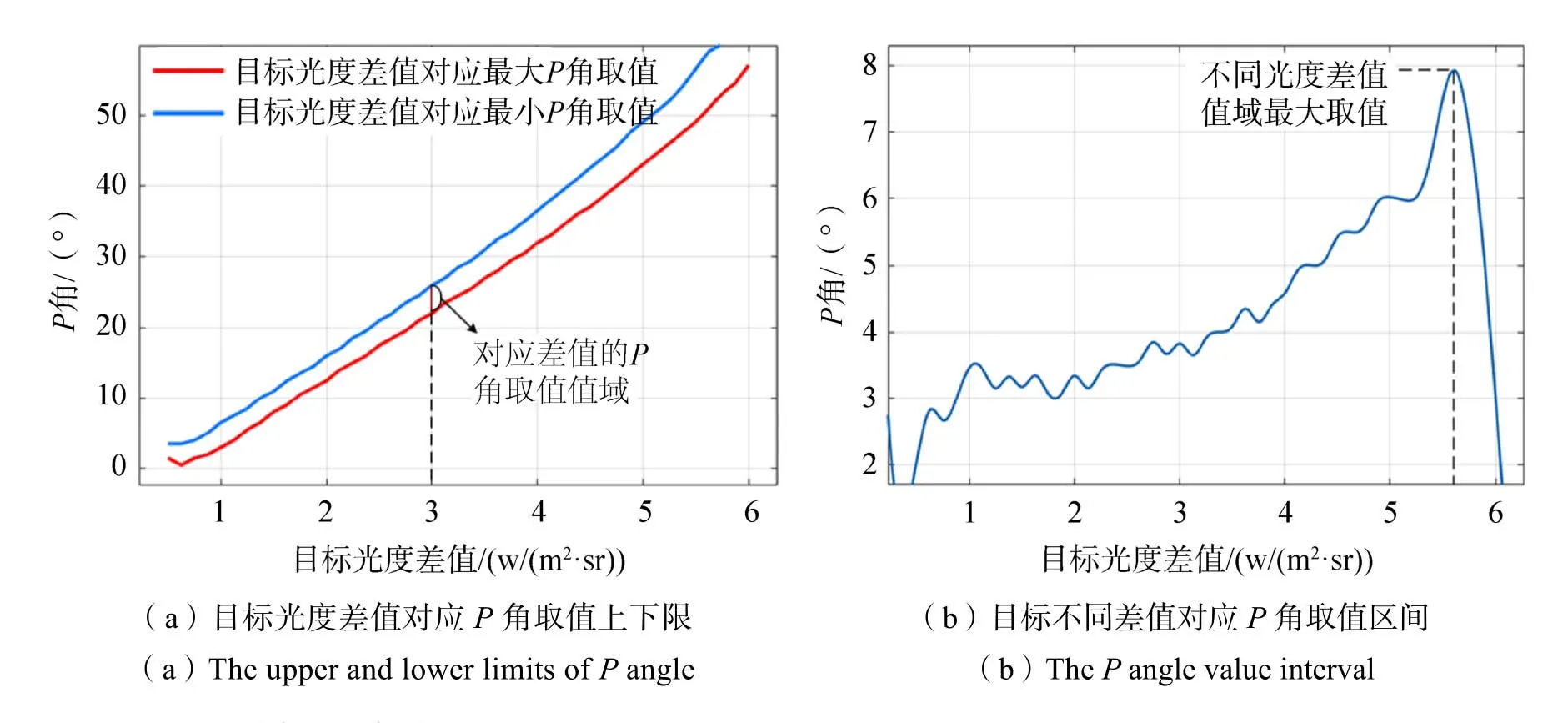
图10 遍历目标光度差值确定的旋转轴与探测方向间夹角（P 角）取值区间Fig.10 The P angle value interval determined by traversing the target photometric difference

对于不同的收发角度，遍历不同旋转轴指向变化进行周期光度信息仿真，重复前段步骤求取光度差值波动值域并反演确定其旋转轴与探测方向夹角的取值区间。图11 为收发角5°及20°下的旋转轴方位角、P角变化与光变差值的三维曲线，可见同一光度差值对应的波动值域随着收发角度的增大而增加，增至20°条件下的波动值域已明显增大，此时进行反演得到可缩小的P角取值范围明显减小。收发角度大于20°后的变化幅度不易区分，不再明显简化轴向遍历效率。

上述结论可在旋转轴指向提取中加以应用，以旋转轴与探测方向间夹角为区分标准，在确定光源与接收装置间收发角度的情况下快速缩小区分区间，达到简化提取流程和提高效率的目的。但也存在如收发角度不能过大、需已知一定的目标碎片先验信息、难以对极不规则碎片进行分类等局限。

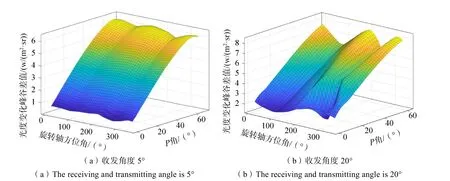
图11 不同光源与接收装置间收发夹角下的光变差值随轴向相位角、方位角变化Fig.11 Three-dimensional graphs of the light curve variation between the phase angle and the azimuth of the rotation axis

4 结束语

分析旋转空间碎片的光变规律对于更精确、高效地提取碎片旋转参数具有重要意义。本文提出了一类典型碎片的光度探测仿真模型的搭建方案，分别在旋转轴与探测方向间夹角持续变化和稳定不变的条件下对不同旋转态碎片作全周期光度信息模拟，确定了不同旋转状态下的光度峰谷差值变化规律，并通过光度变化分析近场模拟试验进行验证；在不同的收发夹角下进行仿真，寻找可有效缩小旋转轴向存在的取值范围，与理想收发状态下任一光度差值对应的旋转轴与探测方向间夹角kα相比，在收发角度5°下可将此夹角的取值区间缩小在kα±4°以内，取值区间随收发角度增大而增加，由此简化遍历式旋转轴向提取流程，提高轴向提取效率，为提取碎片目标旋转轴向流程提供了简化思路与参考。