可返回高超声速巡航飞行器轨迹分步与多目标优化
2020-07-09王开强张柏楠
王开强 张柏楠
(中国空间技术研究院载人航天总体部,北京 100094)
0 引言
随着超燃冲压发动机的发展,高超声速巡航飞行器逐渐进入科研人员的研究视线。其推进效率相比于传统火箭得到大幅提高,可在20km 以上的高度进行马赫数大于5 的高超声速巡航飞行,随后返回地面的预定机场水平着陆,在未来的空基发射入轨领域具有很好的发展前景。目前,仅有美国X-43 高超声速试验飞行器实现了10s时间量级、马赫数大于7 的稳态巡航飞行[1]。对于可返回高超声速巡航飞行器,其飞行阶段较多,且各阶段均包含了众多不同类型的约束条件。因此其飞行轨迹设计较为复杂,需要借助优化的方法手段。
目前,国内外已开展了一些关于巡航轨迹优化的研究。文献[2-3]采用差分进化算法和MATLAB 优化工具箱等,对高超声速乘波体飞行器在周期性巡航和稳态巡航2 种模式下的轨迹优化问题进行了研究。文献[4-5]基于航空交通管制规则,采用分支定界法对民航飞机的巡航程序和轨迹进行了优化。文献[6]基于EUROCONTROL’S 软件的模型和优化算法,考虑风的影响,得到了不同巡航高度下飞行时间和耗油量最优的轨迹;文献[7]采用模式搜索的确定性算法对巡航轨迹进行了优化,以改善民航飞行管理;文献[8]同样应用确定性优化算法,对定高巡航飞行轨迹优化算法进行了研究;文献[9-13]仅针对高超声速周期性巡航轨迹进行了优化研究;文献[14]采用遗传算法对平流层飞艇的巡航机动航迹进行了优化。目前已有的这些研究大多仅仅针对巡航段,采用不同的直接法、间接法,配合不同的优化算法,进行轨迹设计优化。
关于高超声速巡航飞行器全轨迹优化方面,目前的研究较少。仅有文献[15]将其飞行轨迹分为助推段、上升段、巡航段、俯冲段4个阶段进行优化,其中巡航段事先人为确定了一个固定的巡航高度、马赫数等,以便于进行其它飞行阶段的优化。轨迹多目标优化方面,国内已有一些关于高超声速再入飞行器的相关研究[16-18],尚无针对高超声速巡航飞行器的轨迹多目标优化研究。实际上,可返回的高超声速巡航飞行器相比于再入飞行器,其飞行阶段划分更多,各阶段可能存在独特的优化目标,并且各阶段之间可能存在一定的先后顺序和耦合关联,因此有必要对该类飞行器的全飞行轨迹开展分步与多目标优化研究。
本文面向空基发射入轨任务,对配置超燃冲压发动机的可返回地面预定机场的高超声速巡航飞行器全轨迹分步与多目标优化问题进行研究。首先,对本文使用的飞行动力学模型、飞行器模型和地球物理模型进行介绍。其次,对整个全轨迹分步多目标优化问题进行描述,对轨迹分步多目标优化的策略步骤、优化算法、优化建模等内容进行说明。然后,对剩余段轨迹多目标优化中采用的第三代直接搜索域(Directed Search Domain-III,DSD-III)的经典多目标优化算法进行简要描述。最后给出优化算例和仿真结果,并基于得到的多目标优化解集在设计空间中的分布特性,进一步分析设计解选择决策的建议,为实际工程设计提供参考。
1 飞行动力学模型及方法
1.1 动力学方程
本文采用经度—纬度—高度3个变量描述飞行器质心在三维空间中运动的位置信息,采用的动力学方程如下(其中考虑了地球扁率,以及地球自转引起的牵连加速度和科氏惯性加速度)
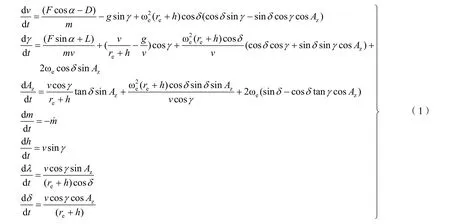
式中t为飞行时间;v、γ、Az、m、h、λ、δ分别为飞行速度、航迹倾斜角、速度方位角(也称航向角)、飞行器质量、高度、经度和纬度,这7个变量构成了本文飞行器飞行轨迹的状态变量;F为发动机推力;m˙为发动机质量流量;α为飞行攻角;g为地球重力加速度;ωe=7.292×10–5rad/s 为地球自转角速度;re为地球半径;D、L分别为飞行过程中受到的气动阻力和升力,可由公式计算得到

式中Ar是飞行器的参考面积;CD、CL分别为阻力系数、升力系数,一般由马赫数、飞行攻角计算得到,或在各系数随马赫数和攻角的二维插值表中进行线性插值得到;q为动压为大气密度)。
1.2 发动机模型
本文飞行器在助推爬升段和巡航飞行段分别使用固体火箭发动机、超燃冲压发动机进行飞行。对于固体火箭发动机,为便于分析计算,假设其推力和比冲均为一恒定值,因此有

式中ve为发动机比冲,单位为m/s。
对于超燃冲压发动机,本文根据桑格尔的发动机数据表[19],通过线性插值得到推力和质量流量。其中,插值变量为马赫数Ma、高度h、攻角α。
1.3 质量模型
飞行器包含固体火箭助推器(包含过渡段)和巡航飞行器本体2 部分,整个组合体在发射时刻的初始质量m0如下

式中m1d、m1p分别为助推器干质量和推进剂质量,m2d、m2p分别为飞行器本体干质量和燃料质量。
当固体助推器结束工作转入无动力滑行段时,固体助推器被抛离,此时无动力滑行段初始时刻飞行器的质量m02为

1.4 地球物理模型
本文采用J2引力模型描述重力加速度和地球半径

式中μe=398600km3/s2为地球引力常数;J2=1.08264×10–3为J2引力常数;ra=6378.135km 和rb=6356.912km分别为地球赤道半径和极半径。
大气模型采用美国SA76 模型,其根据飞行高度计算得到大气密度ρ和大气温度T,此时一定高度上的声速vs可由公式(7)[15]计算

2 轨迹分步多目标优化问题
2.1 飞行剖面
本文中飞行任务剖面与美国X43 的飞行过程类似,不同的是本文中的高超声速巡航飞行器需安全返回至地面预定的机场着陆。整个飞行剖面主要分为以下5个阶段,如图1 所示。
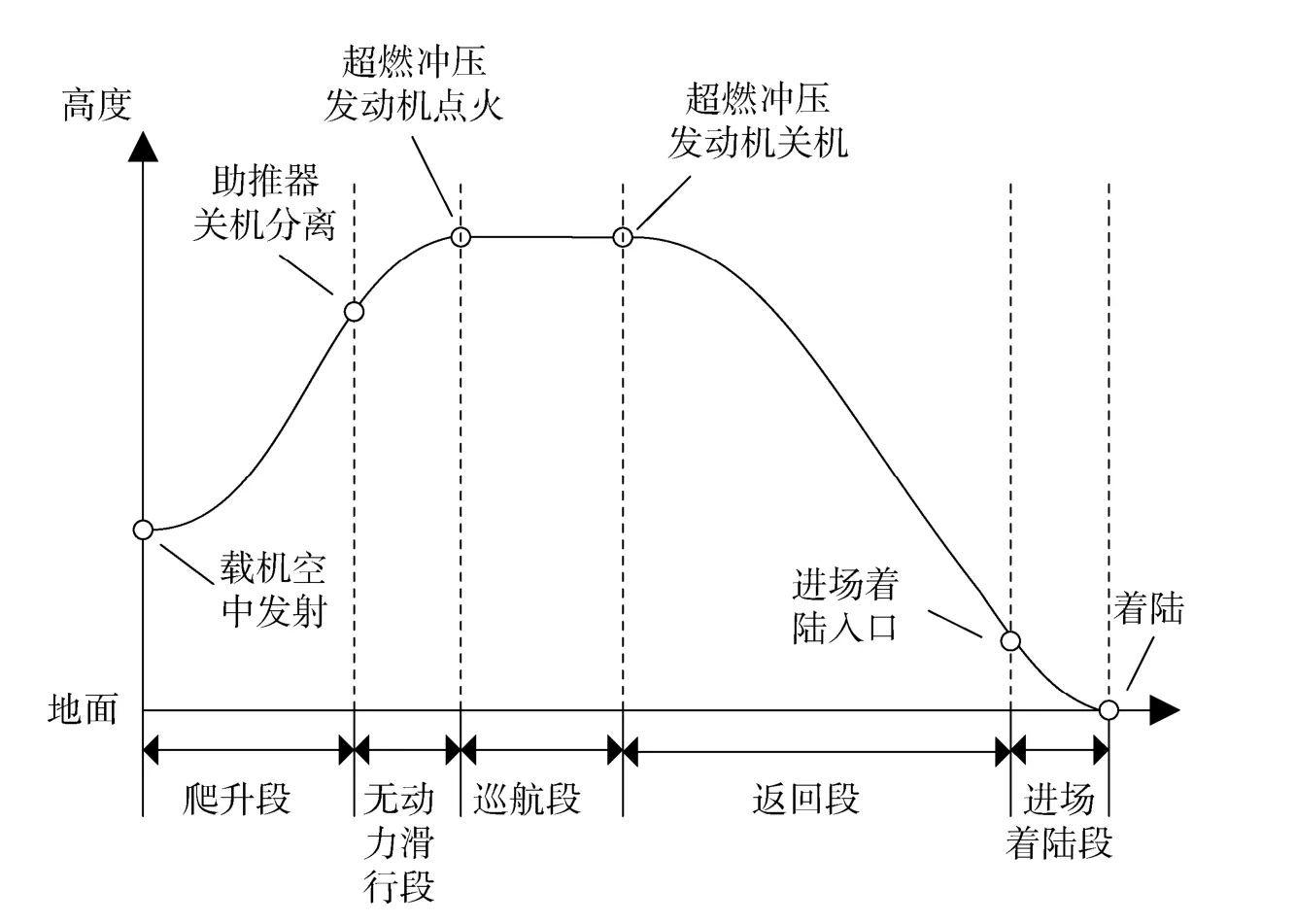
图1 飞行剖面Fig.1 Flight profile
1)爬升段:整个固体火箭助推器与飞行器的组合体由载机运送至高空进行空中发射,然后在固体助推器的作用下进行爬升,直至推进剂燃尽后关机,并与飞行器本体分离。
2)无动力滑行段:飞行器本体与助推器分离后,进行无动力滑行至规定的巡航高度和马赫数。
3)巡航段:飞行器的超燃冲压发动机点火,进行定高定速的稳态巡航飞行,直至燃料燃尽后关机,巡航段结束。
4)返回段:飞行器向预定的着陆机场进行无动力的返回飞行,并达到规定的进场着陆入口飞行状态。
5)进场着陆段:飞行器瞄准着陆机场,通过变换下降飞行的轨迹策略,逐步降低高度和速度,并调整航迹倾斜角,直至在机场着陆。
本文轨迹优化中,将爬升段和无动力滑行段合并为爬升滑行段进行优化。此外,进场着陆段的飞行轨迹设计方法较为特殊,与前面各飞行阶段完全不同,不属于本文研究的范畴,因此本文的轨迹优化仅包含爬升滑行段、巡航段和返回段。
2.2 轨迹分步多目标优化
本文将整个轨迹优化分为第一步巡航段优化和第二步剩余段优化两步依次进行,各段有其对应的优化目标。主要有以下两方面考虑:
1)从飞行任务层面,空基发射入轨任务中,巡航段是最主要的飞行阶段,入轨飞行器的空基投放就是在该段完成。因此,巡航轨迹与飞行主任务直接相关,应首先予以优化确定。
2)从轨迹优化步骤层面,剩余飞行段的轨迹优化须基于巡航飞行状态进行。其中爬升滑行段需要初始巡航飞行状态作为其轨迹优化的终端状态约束,从而在该段结束时顺利转入高超声速巡航飞行;而返回段的轨迹优化则需要以巡航段结束时刻的飞行状态作为状态变量的初始值。因此,巡航飞行状态也是其它飞行段轨迹优化的前提基础。
整个轨迹分步多目标优化的流程如图2 所示。首先对巡航段飞行轨迹进行单目标优化,得到最优巡航初始飞行状态参数。然后基于此进行剩余段的轨迹多目标优化,其首先根据最优初始巡航状态进行爬升滑行段的轨迹优化;然后进行巡航段飞行仿真,得到巡航段结束时刻的飞行状态参数;最后基于此进行返回段的轨迹优化,最终得到整个飞行轨迹。
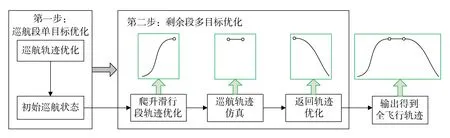
图2 分步轨迹优化流程Fig.2 Procedure of multistep trajectory optimization
优化算法方面,第一步巡航段轨迹单目标优化采用序列二次规划算法(Sequential Quadratic Programming,SQP);第二步剩余段则采用经典多目标优化方法中的第三代直接搜索域法DSD-III[20-21]。
2.3 各段优化目标讨论
(1)巡航段优化目标
巡航段的优化目标对应于飞行任务级目标。在本文针对的空基发射入轨任务中,为入轨飞行器提供更多的初始机械能是其追求的目标。
(2)剩余段优化目标
剩余段轨迹优化的目标是减小爬升滑行段和返回段的飞行难度,在保证达到规定巡航飞行状态要求的前提下,减小整个飞行任务执行的难度。本文主要从驻点峰值热流密度和轨迹振荡程度两方面评价飞行难度,并作为优化目标考虑:
1)驻点峰值热流密度最小:为了减小高超声速巡航时的阻力,巡航飞行器的外形非常扁平,因而其前缘驻点处的半径很小,此时飞行过程中的驻点热流密度较大。根据X43 飞行器的相关数据[22],其在30km以马赫数7 和2°攻角进行巡航时的驻点热流约为6.2MW/m2。因此,本文研究的这一类巡航飞行器中,驻点峰值热流问题较为突出,应予以优化减小,从而减轻对结构热防护的设计压力。
2)轨迹振荡最小:爬升滑行段和返回段的飞行可能出现一定的轨迹振荡,频繁、大幅的轨迹振荡对飞行控制不利。尤其在返回段,轨迹振荡可能影响转进场着陆段时的飞行状态,进而对最终的着陆过程产生不利影响。因此,以轨迹振荡最小为优化目标,有助于降低整个任务的飞行难度。
考虑到上述两个优化目标存在此消彼长的制约关系,本文采用多目标优化方法求解剩余段轨迹优化问题,以期得到多目标优化解集(Pareto 非劣解集)。
2.4 巡航段轨迹优化模型
巡航段优化目标为
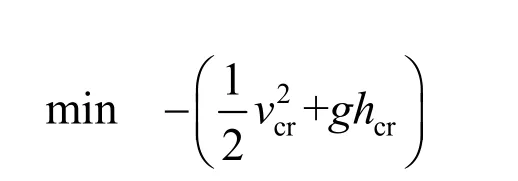
式中vcr和hcr分别为巡航速度和高度。该目标可以在空基发射入轨任务中为入轨飞行器提供更多的初始机械能。
巡航段设计变量为:1)巡航初始时刻的高度h0cr;2)巡航初始时刻的马赫数Ma0cr;3)巡航期间的飞行攻角αcr。在定高定速的稳态巡航模式中,巡航高度和马赫数基本不变。因此由上述3个设计变量即可确定巡航段的飞行状态。三者的取值范围须处于超燃冲压发动机的工作窗口内。本文参考“桑格尔”冲压发动机[19]的窗口参数给出取值范围如表1 所示。

表1 设计变量取值范围Tab.1 Ranges of the design variables
巡航段约束条件为:
1)根据稳态巡航的推阻平衡和升质量平衡条件,得巡航期间飞行马赫数、航迹倾斜角的理论变化量应为零,但在实际飞行中很难保证上述变化量绝对为零,需要给定一个很小的容许变化范围,本文对最大、最小巡航马赫数和以及巡航期间最大航迹倾斜角最小航迹倾斜角作如下限定:
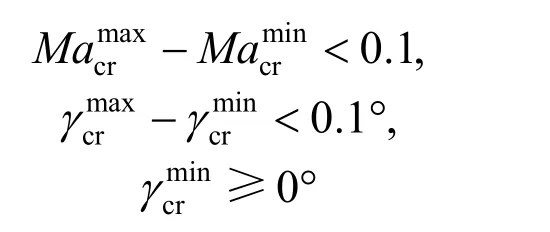
2)动压约束,实际飞行动压q应小于动压约束上边界
3)驻点峰值热流约束,驻点热流Qs的最大值即驻点峰值热流Qsm应小于上边界
2.5 剩余段轨迹优化模型
剩余段轨迹优化为二维多目标优化
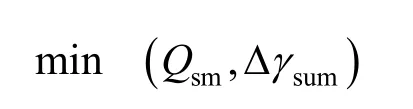
Δγsum为轨迹振荡总量,用航迹倾斜角的全程累积变化量表示

式中tf为全轨迹的总飞行时间。
剩余段轨迹优化的设计变量为:
1)爬升滑行段飞行攻角αcg,取值范围为–10°≤αcg≤25°;
2)返回段飞行攻角αrt,取值范围为0°≤αrt≤5°。
剩余段轨迹优化的约束条件为:
1)动压约束:q≤qub;
2)过载约束:实际过载nload应小于许用过载上限
4)爬升滑行段终端飞行状态约束。爬升滑行段结束时,其高度hfcg和马赫数Mafcg必须与第一步优化得到的巡航段入口高度h0cr和马赫数Ma0cr相等,且此时航迹倾斜角γfcg应基本为0,这里同样设置一个很小的容许范围0.1°,则有以下约束:
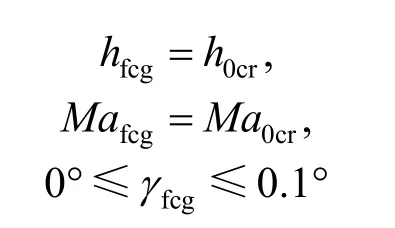
5)进场着陆初始飞行状态约束。本文飞行器最终在地面航程已定的指定机场着陆,因此返回段结束时须满足一定的关于高度、速度、航迹倾斜角和航程的进场着陆条件

式中hfr为飞行高度fh的要求值;和分别为飞行速度vf的上、下边界;和分别为航迹倾斜角γf的上、下边界;和则分别限定了航程xf的上、下边界。
3 多目标优化方法
一个标准的多目标优化问题可由以下形式表达:
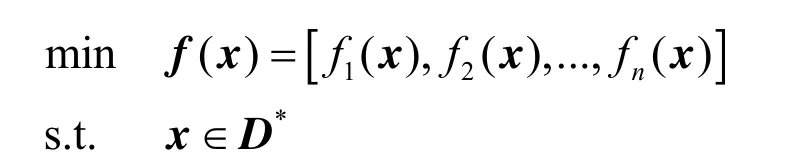
式中x是设计变量;f(x)为多目标函数向量;fi(i=1, 2, …,n)为第i个目标函数;n为目标函数数量;D*是可行设计空间。各目标函数构成了目标空间。满足约束条件的目标空间称为可行目标空间,记为Y*。
多目标优化目标函数中,任意两个目标之间都是此消彼长的制约关系,因此其解不唯一。Pareto 优化解,也称多目标优化非劣解,其对应的所有n个目标函数取值不可能同时小于任何其它优化解对应的相应目标函数值。否则,该解为劣解,不属于Pareto 优化解。
本文采用第三代直接搜索域DSD-III 的经典多目标优化方法。其基于锚点进行多目标寻优。每个锚点对应于一个优化目标的单目标最优解,因此n个目标函数对应n个锚点。例如,在图3 所示的二维多目标优化问题中,f1和f2为两个目标函数,因而总共存在两个锚点。其中,左上方的锚点对应于目标f1最优(最小)时的单目标优化解,而右下方的锚点则对应于目标f2最优时的单目标优化解。过所有锚点可构建一个目标空间,称为理想超平面。在图3 中,该超平面实际为经过两个锚点的直线(图3 中的虚线)。图中左下方黑色曲线段为Pareto 前缘,其中的点构成了Pareto 前缘点集。
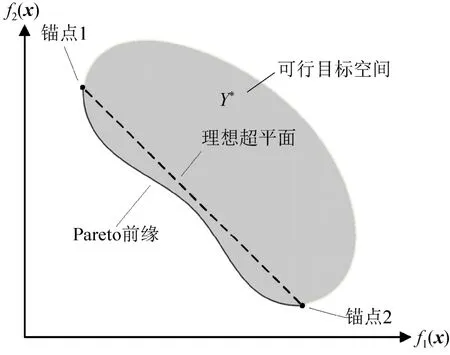
图3 多目标优化的基本定义Fig.3 Basic definitions of MOO
DSD-III 可以较为高效的求得多目标优化Pareto 前缘点集,且该点集能较为全面和均匀的覆盖Pareto前缘。Pareto 点集的分布均匀性,能够以有限的点表征优化目标之间的量化制约变化信息,为进一步对优化解的选择和决策提供支持。有关该方法的详细描述可参阅原始文献[21]。
4 算例及优化结果
4.1 算例描述
算例中的助推器及巡航飞行器各部分质量如表2 所示。巡航飞行器由载机进行空基投放发射,投放高度为12km,投放初速度为236m/s,初始航迹倾斜角为5°。其中,固体火箭助推器总推力为240kN,比冲为2893m/s。

表2 助推器及巡航飞行器质量Tab.2 Mass of booster and the cruise vehicle单位:kg
约束条件方面,动压约束设置为不超过qub=130kPa,过载不超过5,驻点峰值热流小于5MW/m2,进场着陆初始状态约束参考航天飞机[23]设置如下:

4.2 优化结果
本文采用MATLAB R2016a 软件进行整个优化过程的仿真计算。其中采用了fmincon 优化器,选用SQP 算法作为底层的单目标优化算法。
(1)第一步优化结果
第一步巡航段单目标最优轨迹如表3 所示,飞行器巡航期间高度和马赫数基本不变,满足稳态巡航的状态要求。

表3 巡航段优化解Tab.3 The cruise optimal solution
(2)第二步优化结果
基于上述巡航飞行状态,得到的剩余段轨迹二维多目标优化Pareto 前缘点集如图4 所示。其中,所有点均为有效点,未得到冗余的优化点。同时,该前缘点集较为均匀的勾勒出了该多目标优化问题的Pareto 前缘,其变化趋势具有较强的非线性。分析该Pareto 点集的分布可知,在图中左侧驻点峰值热流Qsm较小的区域中,随着航迹倾斜角全程累积变化量Δγsum的大幅降低,Qsm的增加量很小。而随着Qsm的增加,航迹倾斜角累积变化量的降低幅度逐渐减小。在图4 中的右侧,当Qsm>4.35MW/m2时,降低Δγsum需要付出的热流代价较高。因此在设计解的选择和决策时,建议在Pareto 前缘点集分布图中相对靠左的区域(Qsm<4.35MW/m2)选择设计解,避免热流代价很高的设计解区域。最终的设计解,还需进一步结合防热技术发展现状和实际工程具体设计需求进行分析确定。

图4 剩余段轨迹优化Pareto 前缘点集Fig.4 Pareto frontier set of rest trajectory optimization
图4 中位于最左上方的Pareto 点对应于驻点峰值热流Qsm最小的单目标优化解,最右下方的Pareto 点则对应于轨迹振荡程度Δγsum最小的单目标优化解。两者的对比如图5 所示,主要轨迹参数如表4 所示。
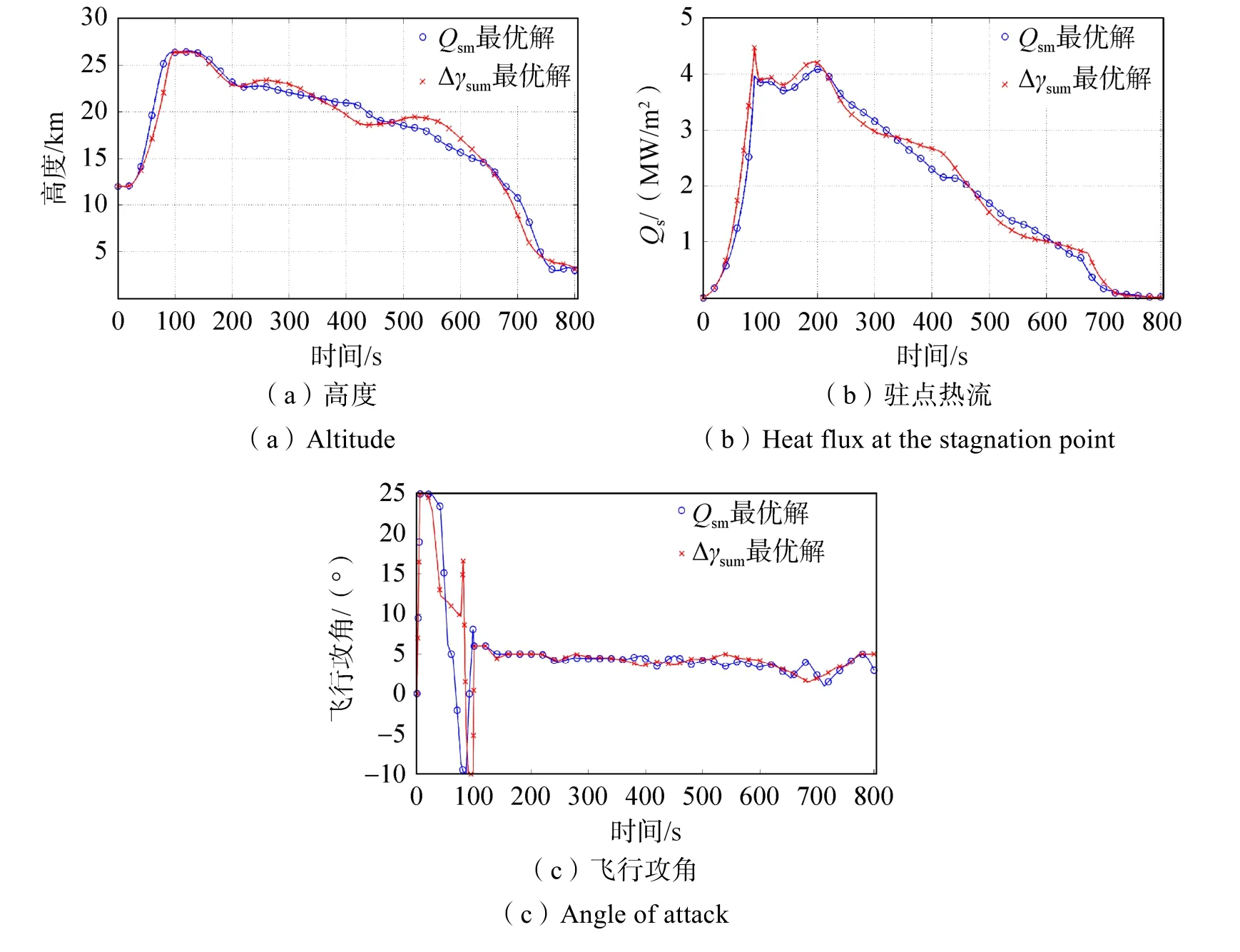
图5 两个轨迹优化解对比Fig.5 Comparison of the two optimal trajectories
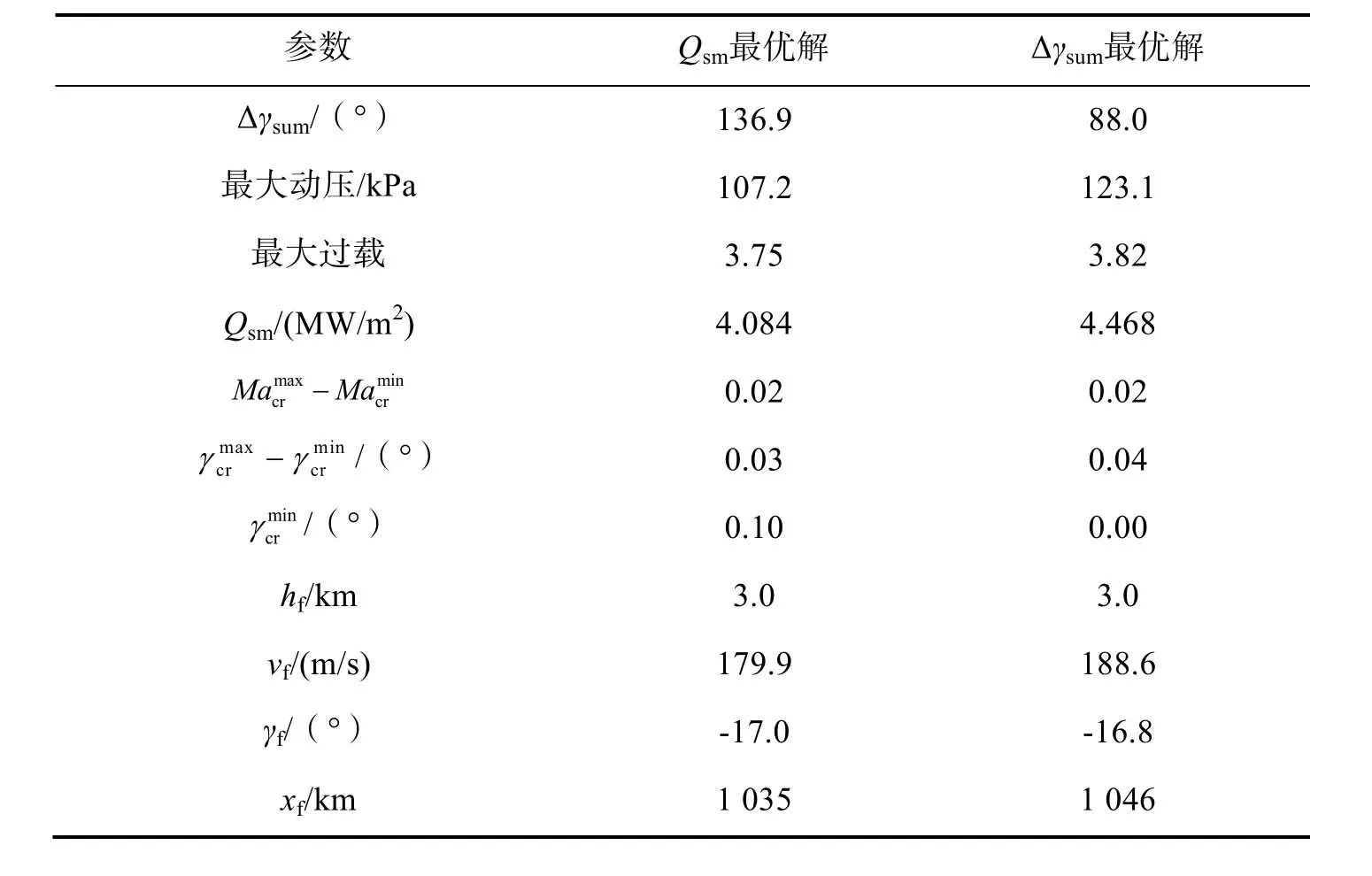
表4 轨迹参数Tab.4 Trajectory parameters
由表4 所示数据可得,所有约束条件均满足,且剩余段轨迹多目标优化结果体现了两个优化目标的最优性以及两者之间量化制约变化关系。其中,将Qsm最优解和Δγsum最优解进行相互对比可知,两者分别将各自的优化目标Qsm和Δγsum相对削减了8.6%和35.7%。
此外,结合图5 的飞行攻角曲线可以看出,在两条最优轨迹中,作为设计变量的爬升滑行段(100s以前)飞行攻角存在明显的不同;而返回段(120s 以后)的飞行攻角在初期较为近似,350s 后逐渐显现出差异。因此,两条轨迹的设计变量对于优化目标寻优的期望值差异主要集中在爬升滑行段和返回段中期以后的飞行过程。
5 结束语
本文面向空基发射入轨任务,对配置超燃冲压发动机的可返回高超声速巡航飞行器的轨迹多目标优化问题进行了构建、分析和求解,该飞行器须在巡航结束之后减速返回地面预定机场水平着陆。首先将高超声速巡航飞行器的轨迹设计划分为巡航段轨迹单目标优化和剩余段轨迹多目标优化两步先后进行,其次对各段飞行轨迹优化模型进行了定义,最后应用SQP 优化算法和DSD-III 多目标方法对整个轨迹优化问题进行了求解。
研究结果表明,针对高超声速巡航飞行器,采用分步进行多目标优化的策略,可以协调处理其不同阶段飞行轨迹之间的关联关系和各飞行阶段的不同优化需求,并将整个轨迹设计问题转换为具体模型化表达的优化问题。通过采用相应的优化算法,求解各段飞行轨迹优化问题,最终综合形成完整的飞行轨迹优化解。优化方法层面,在剩余段轨迹多目标优化中,采用DSD-III 方法优化得到的Pareto 前缘点集无冗余优化点,且较为均匀的描绘出了多目标优化问题的非线性Pareto 前缘;两个优化目标均取得了不同幅度的优化效果,所有约束条件均满足要求,可有效求解该轨迹多目标优化问题。本文的研究成果可为类似的实际工程优化设计提供一种从问题构建、到采用相关优化算法进行求解、再到根据多目标优化结果进行制约权衡设计的设计思路和参考范式。
