源自考题 探索变式
2020-07-08赵金丽
赵金丽
(浙江省杭州市余杭中学,311120)
《普通高中数学课程标准(2017年版)》提出,要注意培养学生的数学核心素养.在课堂上渗透数学核心素养,让学生不断体验数学学习的过程,从而培养新时代学生的自我学习研究能力和创新活力是重中之重.
课堂形式是多样的,一般来讲,可大致分为新授课、综合应用课和试卷评价课.而在试卷评价教学中,可以选择一个题目或一类题型展开变式教学.本文以浙江省2017年高考题为载体,探索研究变式教学的方法.
一、原题呈现
2017年浙江省高考数学简答题的第2题,使得很多学生在该题上思维受阻,原因是用向量法建系时很难让所有坐标轴落在四棱锥的边上,以常规方法建系时四棱锥的顶点不能在z轴上,而用几何法找角时又不能直接通过斜线上的一点去作该面的垂线,因此有一定的难度.原题呈现如下:
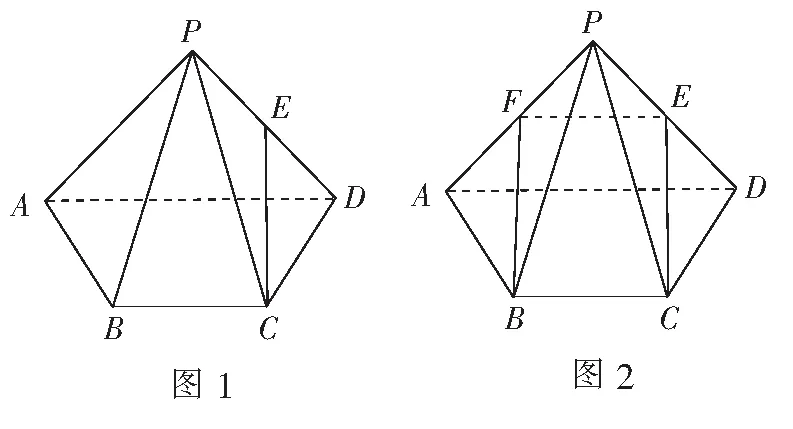
如图1,已知四棱锥P-ABCD,∆PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(1)证明:CE∥平面PAB;
(2)求直线CE与平面PBC所成角的正弦值.
分析第(1)问可运用几何法,即用线面平行的判定理.第(2)问给出两种方法解决,运用向量法和几何法找到线面角求值,关键就是找线面垂直,而这种垂直往往会利用面面垂直的性质定理.
解析(1)证明:取AP的中点F,连结EF,FB,如图2所示.由于EFBC,所以四边形EFBC是平行四边形,则CE∥BF.又因为CE⊄平面PAB,BF⊆平面PAB,由线面平行的判定定理,可知CE∥平面PAB.
(2)方法1(几何法)
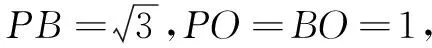
所以CE2=CD2+ED2-2CD·EDcos∠PDC

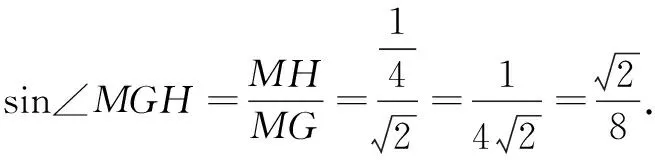
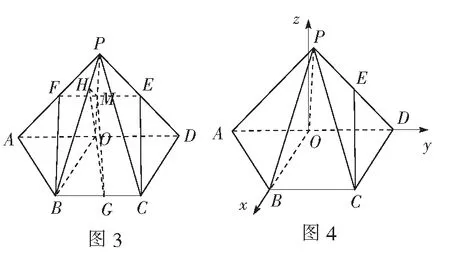
方法2(向量法)
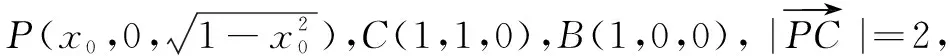
二、变式训练
变式1如图5,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AD=2,BC=CD=1,AD∥BC,E是PD的中点.
(1)证明:CE∥平面PAB;
(2)若∠DAB=60°,求BE与平面PBC所成角的正弦值.
解题指导(1)证明线面平行,一般通过线面平行的判定定理或者面面平行的定义得到,因此可以从这两个方面入手.本题可以在平面PAB中找一条与CE平行的直线,通过线面平行的判定定理得到.(2)求线面角可以通过几何法找到线面角求出,或者通过等体积法求出高,再求出线面角,也可以通过建系,用向量法,最后代入线面角的公式求出.
解题过程略.
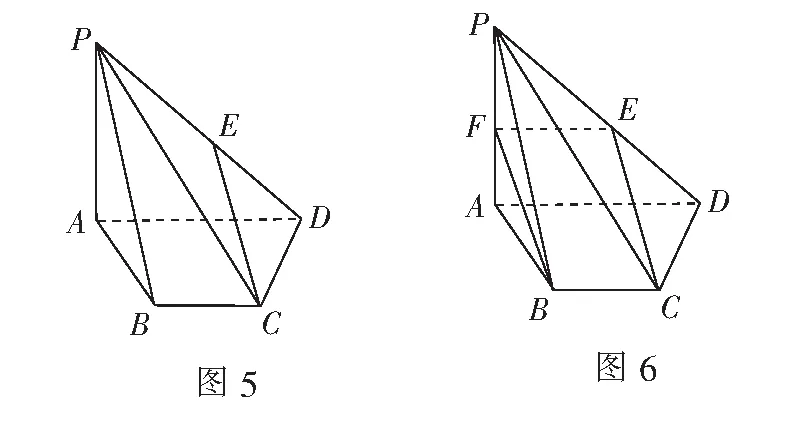
变式2如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AD=2,BC=CD=1,AD∥BC.
(1)若E是PD的中点,证明:CE∥平面PAB;
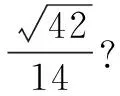
解析(1)证明:在AP上取中点F,连结EF,BF,则EFBC,所以四边形EFBC是平行四边形,所以CE∥BF.又因为BF⊂平面PAB,CE⊄平面PAB,所以CE∥平面PAB.
(2)方法1(空间向量法)


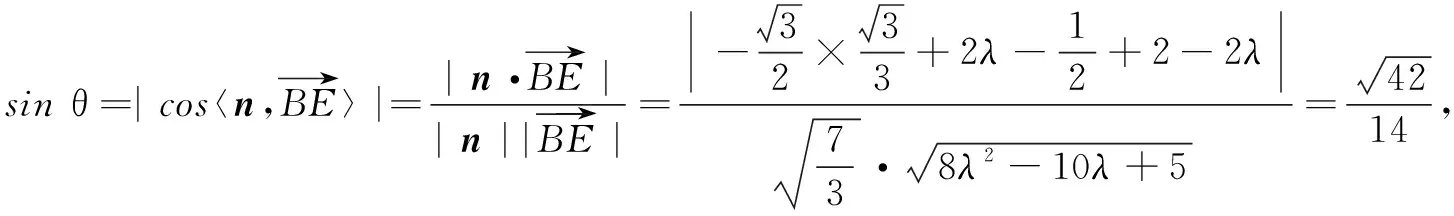
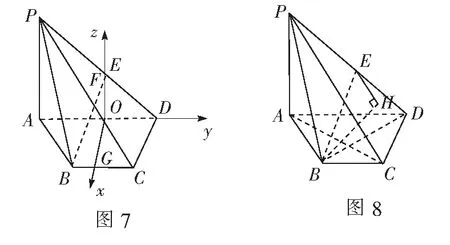
方法2(等体积法)
如图8,过点B作BH垂直平面PCD,连结EH,则∠BEH即为直线BE与平面PCD所成角.
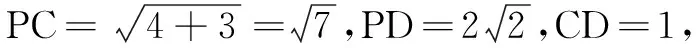
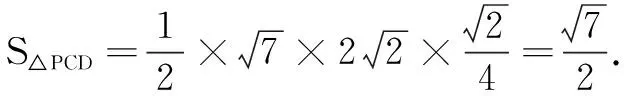
在立体几何题上采用一题多解,由根生叶,并设置开放性问题,把学生带入立体几何的海洋中遨游,可以培养学生发现问题,分析问题,解决问题的能力,同时也有助于六大核心素养的渗透.
