“双轨模型”的教学设计与思考

郭红清

(江苏省黄埭中学，215143)

数学建模、模型应用是数学核心素养中的重要组成部分.每一个典型问题的解决，其实都是典型的解题实践,蕴含着深刻的模型思想.知识无涯,题海无边,不可能逐一解决每一道数学题,因此，具有普遍意义的方法论和数学观就显得非常必要.本文以解析几何中的存在性问题为例，探究复习课“双轨模型”的教学设计.

一、创设情境,模型建构

活动1已知∆ABC的三条边长a,b,c,作出三角形图形.

分析画出线段a即BC以后,我们就已经确定了所求三角形的两个顶点B,C,意味着再确定一个顶点A就行了.

条件包含两部分AB=c和AC=b,条件的每一部分单独使用不能完全确定点A,只能确定它在一个“轨迹”上.综合起来,点A应该是两个“轨迹”的交点.尺规作图大体上都是这样的过程.

受以上作图过程的启发,我们抽离出一个解题模型——“双轨模型”,加以推广,能解决很多的数学存在性或有解的问题,尤以解析几何问题最为典型.模型叙述如下:

首先,把问题归结要确定一个点；然后,把条件分成两部分,使得对每一部分,未知点都形成一个轨迹.未知点的存在就意味着两部分对应轨迹的公共点,也即转化为图形的位置关系.

设计意图尺规作图是平面几何教学的传统内容,形象生动的背景切入,贴近学生认知,简单易懂却又深刻.作图方法在理论上的重要价值特别能启发解题思路,使得学生建构和接受“双轨模型”非常自然,为后续迁移和应用做好铺垫.

二、类比推理,模型迁移

活动2(1)直线y=kx+1与圆(x-2)2+y2=1有公共点,求实数k的取值范围.

(2)在平面直角坐标系xOy内，已知点A(2,0),在直线l:y=kx+1上存在一点P,使得PA=1,求实数k的取值范围.

分析容易发现,两题实质上互通,存在点P即直线和圆有公共点,而位置关系又是直线和圆的根本问题,以下借助模型加以说明.

关于点P的条件分成两部分：一是在直线l上;二是满足PA=1.

只看条件的一部分,将另一部分放在一边,点P既不能完全确定又不能完全自由,那么点P被限制在一个“轨迹”上.条件(2)隐藏着一个以A(2,0)为圆心,半径为1的圆A.点P的存在转化为直线和圆A两个轨迹必须有公共点.

设计意图通过两个本质相同的实例对比,从形式上的不同认识到实质上的一致,体会存在性问题的描述方式,紧扣教材中直线和圆的位置关系,引导学生从逻辑关系上打通两者的联系.(2)中隐藏了一个圆,为增加难度,可以考虑将条件“PA=1”修改为“OP=2AP”.修改后难度更高,条件“OP=2AP”需要采用坐标法得到代数方程,进而通过方程认识到本题中隐藏的轨迹,这也是考试热点“阿波罗尼斯圆”.

三、巩固深化,模型应用

活动3(1)已知点P是圆O:x2+y2=4上的动点,点A(4,0),若直线y=kx+1上总存在点Q,使点Q恰是线段AP的中点,求实数k的取值范围.

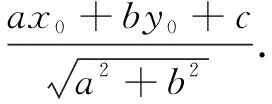
分析(1)关于点Q的条件分成两部分：① 在直线y=kx+1上;② 满足点Q恰是线段AP的中点.为了认识条件②,利用解析法,设出点Q的坐标,利用几何关系中点得出点P,代入已知圆O.第(2)题同理设出点C的坐标，表示有向距离之和为0并化简，即可分析出隐藏的轨迹.

解题过程(1)设Q(x0,y0),点Q恰是线段AP的中点,则P(2x0-4,2y0).

故存在点Q等价于直线y=kx+1与圆(x-2)2+y2=1有公共点.

(2)设C(x0,y0),直线m:y=k(x-3).

化简得y0=k(x0-9).

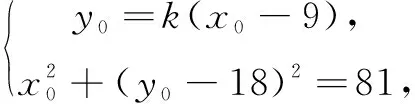
故存在点C等价于直线y=k(x-9)与圆x2+(y-18)2=81有公共点，

设计意图从两个具体的实例入手,抓住双轨模型分析存在性问题的重难点,也即找到题目中隐藏的“轨迹”,两个问题各自隐藏了“圆”和“直线”,具有代表性.问题(1)实质上是活动2中的问题,改变了面貌.问题(2)提供了新概念,要求很高.问题的实质也就是两个轨迹有公共点即直线和圆的位置关系.

四、链接高考,模型追击

活动4(2016年江苏高考题)如图1,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).

(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;

(2)设平行于OA的直线l与圆M相交于B,C两点,且BC=OA，求直线l的方程;

(1)，(2)解题过程略.

解题过程(3)设P(x1,y1),Q(x2,y2),

将(x2,y2)代入已知圆M的方程，得(x1-t-4)2+(y1-3)2=25.点P满足

故圆M上存在点P,Q等价于圆M:(x-

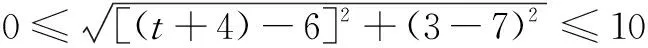
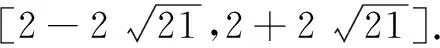
设计意图本题利用几何法解释略有不足,作为解析几何的核心思想,应培养或引导学生多从代数角度思考,即利用坐标法.代数法推理严谨,常常能弥补观察的局限性,回避复杂的几何特征.坐标法可以挖掘题目所蕴含的轨迹方程或代数关系,通过轨迹方程揭示隐藏的图形或轨迹,回到本质的位置关系.

“轨迹”实际上就是点的集合,加以推广,“两条轨迹存在交点”与“两集合交集非空”实质上也是相同的.对于集合A∩B≠∅,借用教材中“含有一个量词的存在性命题”,我们给出数学形式:∃x∈A，使得x∈B.由此来看,存在性问题利用双轨模型来解释实在合理不过.

举一举生活中的情境,两个人的朋友各自构成了朋友圈,所谓存在共同的朋友即意味着两个朋友圈有重叠,从数学上看即两个集合有交集.数学知识来自于生活的高度抽象,而数学方法仍然是实际的抽象.知识和方法都是模型建构的范围,数学核心素养中着重强调建模能力,用数学的眼光看世界.“双轨模型”的学习,在课堂上或课后引导学生从集合,从生活等角度观察,学生思维一定会愈加开阔.