基于“主题式”的课堂教学设计——以“圆锥曲线的参数方程复习”为例

张启锋

(福建省永定第一中学，364100)

“主题”就是指一节课的“中心思想”,好的主题教学应当是和课程知识点紧密吻合的,主题完成的同时也完成了知识点的教学,同时也推动了主题的深入.《普通高中数学课程标准》(2017年版)指出,教师应把主题的内容视为一个整体,引导学生寻找不同量之间的依赖关系、对应关系.教师要理解数学学科素养的具体要求,不仅关注每一节课的教学目标,更要关注主题单元的教学目标,明晰这些目标对实现数学核心素养发展的贡献.主题可以是一章或跨几章内容组成，或一个教学周期内容组成，或以蕴含在一些章节重要数学概念，或培养某个数学核心素养、基本能力组成主题等等.

本文以笔者应福建省教育学院数学研修部之邀,为“2019年福建省普通高中高级职称教师省级培训”开设的一节展示课为例,探索基于“主题式”课堂教学的设计与实施.

一、知识回顾

章建跃博士认为,“概念教学的核心是引导学生开展概括活动:将凝结在数学概念中的数学思维活动打开,以若干典型具体事例的属性、抽象概括共同本质属性、归纳得出数学概念等思维活动而获得概括过程.”通过一定的情境或有效提问,回顾已学的有关概念,为快速进入主题铺路.

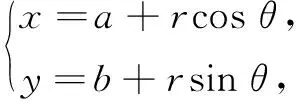
问题1圆与椭圆的参数方程是唯一的吗?

问题2圆锥曲线的参数方程与普通方程如何互相转化?

设计意图学生已学过圆与椭圆的参数方程,从学生已有的基础出发,复习圆锥曲线参数方程与普通方程的互相转化以及参数的几何意义,唤起学生回忆；加深对圆与椭圆参数几何意义的理解,为本节课主题进入做好工具准备,实现追求学生知识的自然生长.

二、方法构建

圆锥曲线的参数方程用来表示圆锥曲线上的点在解题上具有一定的优越性,能解决在普通方程下不易解决的问题,如有关距离问题、交点问题、最值问题和位置关系问题.下面由例题导入本节课主题,即圆锥曲线参数方程中“坐标法”的应用.

分析这是人教版课本中的例题,题目简洁,但含有信息量大,题中包含椭圆与直线,求点的坐标与距离的最小值.

师：此题的着力点在哪?

生：可以用点到直线距离公式把距离表示出来，设椭圆上动点M的坐标.

师：如何表示椭圆上的点?

生：用“坐标法”表示出椭圆上动点M的坐标.

师：为何要用参数来表示点M的坐标？

生：点M(3cosθ,2sinθ)中只有一个变量θ,可以简化运算.

学生基本上都能求出最小距离,但有部分同学不会求点M的坐标,暴露出学生对三角函数辅助角公式掌握得不够娴熟.

设计意图简单的一个设点坐标,有别于以往的必选内容中的点M(x,y),让学生体会到“坐标法”的好处，强化了参数方程和三角函数辅助角公式的应用,体现教学遵从从低点起步,小步慢走的思想.

三、类比改编

问题3与简单的线性规划进行类比,你能改编出一个题目吗?

学生经过充分的思考后:

师：高考中圆锥曲线主要以圆或椭圆为载体,有关取值范围、最值问题、位置关系等,都可以利用参数方程来表示点的坐标.

设计意图简单的一个设点坐标,体现出参数方程的优越性，让学生在自主探究中领悟“坐标法”的好处,体会“坐标法”在解决类似问题中作用.课堂设计符合学生思维发展规律，通过对问题的载体的改变，问题的设问改变,帮助学生进行知识的迁移,加深对“坐标法”的理解.渗透用代数法解决几何问题的思路,从而培养学生独立思考问题、提出问题、解决问题的能力.

四、 思考探究

典型例题不仅能够巩固、深化知识,更重要的是能够通过例题的“结构”,全面掌握知识应用的不变性、灵活性,也能考查学生综合运用所学知识、思维方法,多角度地观察、思考、发现、分析和解决问题的能力.

师：一个动点变为两个动点,如何处理多个动点问题?

生：设椭圆上的动点M(2cosα,sinα)(α为参数),圆上的动点N(cosβ,3+sinβ)(β为参数,然后利用两点间距离公式，可求出|MN|的取值范围.

生2：不对,这样不又有两个变量了吗?应该把动点M到动点N的距离化归为动点M到圆心的距离,求出|MO|,再加上或减去半径长度,就是|MN|的取值范围.

师：非常好,我们可以把这种方法叫“以静制动”.找到其中的一个不变量,利用化归思想,从而实现快捷解题.

设计意图高考试题设计一般会注重素材选取的普遍性,突出知识体系的完整性和知识间的联系.要求学生能够基于试题情境深入思考,整合所学知识得出结论.本例题力求突出知识间的横向联系和方法上的差异性,让学生在“最近发展区”遭遇问题,在熟悉的问题中感觉陌生,在相似的方法中感受到不相似.引导学生自觉使用“坐标法”解决问题,使参数方程发挥最大作用.在教学过程中要主动渗透数形结合思想,并通过有效提问,让本节课主题更加突出.

五、巩固成果

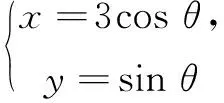
设计意图课堂练习是思维的延续,是检查和发展课堂“主题”是否落实到位、教学目标是否完成的需要.通过高考原题也让学生体会高考怎么考,怎么体现数学核心素养.学生通过练习,在练习中发现易错点,在练习中经历用“坐标法”解决问题的完整过程.

突出坐标法,即用代数方法来解决几何问题.参数就是一座桥梁,是“红娘”.如何发挥“红娘”作用,是本节课自然的、重中之重的“主题”,是最核心的教学要求.例题的精选，让学生感受到借助参数方程设出动点坐标的必要性,体会根据问题的特点选择合适的参数.设出动点坐标,体会解题技巧.而类比改编的设计，能够梳理知识结构,建立知识网络,覆盖基础知识,复习基本技能；能够体现知识的发生、发展过程,逐步深入、层层递进,体现数学思想方法，培养数学核心素养.