思维可视化,让数学学习真正发生
2020-07-07肖丽丹
肖丽丹

[摘要]知识是载体,发展思维是目标,分析思维方法能带动学生更好地掌握具体的知识。“圆的认识”是北师大版小学数学六年级上册第一课时的内容,其实早在一年级甚至入学前,学生就对圆有了初步的认识,但他们对圆的本质特征的认识是模糊的。因此,教学时教师要紧扣圆的本质——到定点的距离等于定长的所有点的集合,即“一中同长”,同时也要考虑学生已有的生活经验,关注学生的思维发展,培养学生的能力,让学生真正参与到数学学习中。
[关键词]圆的本质;思维可视化;思维能力发展
[中图分类号]
G623.5
[文献标识码]A
[文章编号] 1007-9068( 2020)20-0026-02
信息时代发展到今天,学生的知识储备超乎我们的想象,我们的数学课不能再局限于知识的掌握,还要关注学生的学习过程,注重培养学生的思维能力,让数学课变成学生的思维大餐。尤其是概念教学,怎样才能让学生体会所学内容的价值,并经历概念建构的过程,真正理解概念的本质呢?下面,我以六年级“圆的认识”为例,谈谈如何关注学生的课堂交流,让思维可视化,促进学生的思维能力发展。
一、课前思考
关于“圆的认识”这节课的研究有很多,如何才能从众多的研究中找到新方向,让课堂更有深度和广度呢?我以概念的本质和学生的思维特点为突破口,探寻了一条朴实却又不平常的路。
圆的本质是什么?高中课本是这样定义的:在同一平面内,到定点的距离等于定长的所有点的集合叫作圆。简短的一句话包含了两个关键元素——定点和定长,其实就是圆心和半径。因此在教学时要紧紧围绕这两个关键元素开展活动,让学生经历圆的建构过程,对圆的认识从直观表面走向深刻严谨。
二、教学设计
1.情境导入,提出问题
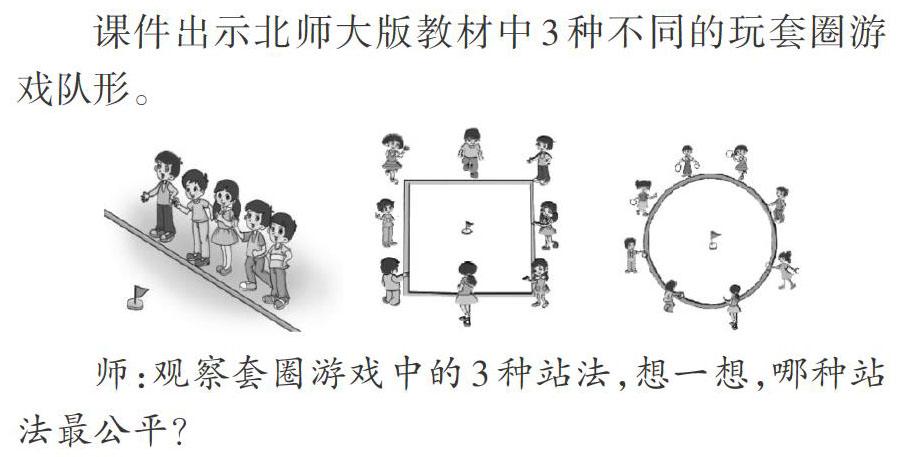
课件出示北师大版教材中3种不同的玩套圈游戏队形。
师:观察套圈游戏中的3种站法,想一想,哪种站法最公平?
(学生各抒己見,经过分析后得出站成圆形时,每个人到旗子的距离相等,所以站成圆形套圈最公平)
师:为什么站成圆形时,每个人到旗子的距离就相等?这节课我们就一起来研究平面上的曲线图形——圆。
这个问题的提出直指圆的本质,但要学生回答还为时尚早,借此引出课题,让学生感受到学习圆的必要性,也揭示了圆是平面上的曲线图形这一特点。
2.认识圆、探索圆
(1)画圆、认识圆
师:你能想办法画一个圆吗?
大多数学生想到用表面是圆形的物体描一圈或用圆规画,如果此时有学生能提出一些独到的方法,就需要教师引导追问,甚至展示。我运用课件动态演示3种画圆的方法:固定拇指,食指转动一圈画圆;固定图钉用线绕一圈画圆;体育老师固定一只脚,手臂伸直,用石灰漏斗在操场上画圆。
师:这3种方法有什么共同点?
学生看了直观动态演示的画圆方法,能很快发现有一个固定不动的点和一个不变的长度,也就是定点和定长,甚至有些学生能直接说出定点是圆心,定长是半径。在学生了解基本的画圆方法后,我示范了圆规画圆的方法,并介绍了圆心、半径和直径的定义,然后让学生自主用圆规画圆,说一说画圆要注意什么。
(2)找圆心
师:玩套圈游戏时,同学们手拉手站成了圆形队形,这时怎样确定旗子的位置呢?
师:假如教具中的圆片就是同学们围成的圆,如何找到它的圆心?请同学们在圆片上找一找。
这个问题比较难,有些学生会用圆规去试一试,也有学生能抓住“直径都经过圆心”的特征,用对折两次的方法找到圆心。学生把圆片对折两次后发现有两条折痕和一个交点,圆心、半径和直径就都出现了。
(3)圆的特点
师:圆的半径和直径还有哪些特点呢?先利用圆片继续折一折、量一量、比一比,再与小组同学说说你发现了什么。
有了前面找圆心活动的基础,大部分学生会继续多折几次,发现圆的半径和直径都有无数条,同一个圆的直径长度是半径的两倍,等等。
师:现在,同学们知道为什么套圈游戏围成圆形时,每个人到旗子的距离都相等了吗?
基于以上探索活动,学生很快就能把每个人到旗子的距离跟半径联系起来,同一个圆内所有半径都相等,回应了情境中提出的问题。
3.生活中的圆
(1)举例说一说生活中的圆。
(2)为什么车轮是圆形的?
(3)猜一猜:车轮在滚动时,轴心的运动轨迹是怎样的?(先让学生谈谈自己的看法,再运用交互式课件演示不同车轮在滚动时轴心的轨迹)
(4)为什么车轮滚动时,圆心的轨迹是一条直线?
(5)解释“一中同长”。
最后两个问题直指圆的核心特征,能帮助学生梳理和综合运用本节课的知识。
4.总结提升
(1)欣赏生活中的圆形物体和运动现象。
(2)从女孩跳芭蕾的矢量运动图中,你能找到几个圆?
三、关注学生,让思维可视化
本节课设计的问题和环节不算多,但好几处学生的回答和展示都给了我惊喜,课堂上生成了很多宝贵资源。
1.当我问学生能想办法画一个圆吗,一位学生说:“先固定一点,再用尺子在它周围量出很多个与它相距4厘米的点,最后把这些点用平滑的曲线连起来。”我眼前一亮,这不正是“到定点距离等于定长的所有点的集合”的画法吗?我赶紧请她展示,并追问:“为什么要画很多个点?为什么它们到固定点的距离都必须是4厘米?能不能有些是5厘米,有些是6厘米呢?”答案是否定的,学生也因此体会到定长的意义。在此基础上,还有学生提出“固定一个点,在它周围可以画很多个大小不同的圆”的想法,衍生出了同心圆。这些画圆方法对学生理解圆的本质有非常好的启发作用,学生从中初步感知了“圆是到一个定点的距离等于定长的点的集合”这一思想。
2.当学生尝试用圆规画圆时,我满以为学生会画得很好,没想到在巡视时,竞发现好些学生画得很吃力。我找出两个具有代表性的错例,让学生说一说是什么原因。经过分析,学生发现一个是定点移动了,另一个是定长变了,所以都没有画成功。善于利用学生的错误资源,就能让学生对定点和定长的意义理解更深刻。
3.在圆片上找圆心的环节,出现了用圆规一点一点尝试的方法,甚至有学生随意画两条线,认为交点就是圆心,当然也有不少学生能想到对折两次找圆心的方法。当这3种方法都展示出来后,我让学生分析哪种方法更好,以及为什么。
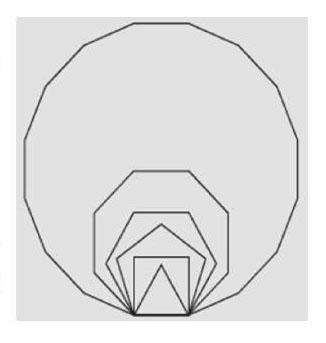
4.小组活动探索圆的其他特征时,我发现有一张学习单上写着:圆是正无限多边形。这是极限思想的体现,很多学生不理解,因此我请这位学生解释什么是正无限多边形。他这样描述:“先把圆片多次对折,然后把边上的点用线顺次连起来,就得到一个正多边形。当边的数量越多,得到的正多边形就越接近圆,所以圆是正无限多边形。”
5.最后我播放课件中女孩跳芭蕾舞的动态矢量图,让学生找一找其中的圆。学生竟然能找出很多个圆:一只脚固定,另一只脚旋转形成一个圆;女孩的裙子本身就是一个圆;她的手保持一个姿势,转动时也形成了圆;脚尖着地旋转时,脚跟的轨迹也是一个圆;旋转时头发甩动也形成了一个圆……可见,学生对圆的本质理解到位了。
当我倾听学生的回答,关注学生的思维方式,尽量让他们展示时,虽然课堂节奏会受到一些影响,但是学生在交流和展示中产生的思维碰撞,却能延伸整个课堂的深度和广度。这样的学习是动态的、真实的。
四、课后反思
虽然本节课的设计没有华丽之处,但我尽力做到将每个环节落到实处。我主要围绕两个问题展开教学:套圈游戏的公平性和车轮为什么是圆的。源于生活的问题情境,让学生体会学习圆的必要性和价值所在。每一个问题都能让学生有话说,当我发现有价值的回答时,会继续追问,引发其他学生的思考,直到问题的本质浮出水面。在找圆心和折圆片的活动环节,我给了学生充分的操作、讨论和交流时间,因此才有类似“圆是正无限多边形”这样精彩的发现。我在处理学生的错误时,不急于给出答案,而是请学生分析原因、辩一辩,印象更深刻。教学之路无止境,当我们关注学生的内心需求和思维方式时,才能让数学学习真正发生。
(责编李琪琦)
