魅力课堂:“可能性”这一课该教什么?
2020-07-07苏明强
苏明强
[摘要]从课程标准的“四基”的角度分析“可能性”这一课,教学的目的应该是让学生了解简单随机现象的不确定性,能说出简单随机现象中所有可能发生的结果,能定性描述简单随机现象发生的可能性大小,体会随机思想和变中不变思想,积累基本活动经验。
[关键词]魅力课堂;可能性;课程标准的“四基”
[中图分类号]
G623.5
[文献标识码]A
[文章编号] 1007-9068( 2020) 20-0017-02
1978年,我国第一次在小学数学中增加了统计知识的教学内容,2001年,教育部颁布了《义务教育数学课程标准(实验稿)》,第一次在小学数学教学内容中增加了概率方面的知识,包括可能性、可能性有大有小、等可能性和可能性大小表示等内容,分布在第一学段和第二学段之中,这时的“可能性”作为概率知识的起始课常常被安排在二年级或三年级。2011年,教育部颁布了《义务教育数学课程标准(2011年版)》,删除了“可能性大小表示”的内容,“可能性”“可能性有大有小”“等可能性”这三部分内容统一安排在第二学段。对“可能性”这一节起始课,北师大版教材安排在四年级上册第八单元第一课时,苏教版教材安排在四年级上册第六单元第一课时,人教版教材安排在五年级上册第四单元第一课时。
对于“可能性”这一课,多数教师反映“教”和“不教”没什么区别,因为即使不教,学生好像也会。于是,教师在教学中基本倾向于让学生学会用“可能”“不可能”“一定”说一句话,如“太阳一定从西边升起来”“太阳不可能从东边升起来”等。这是不是类似语文课中的“造句”?这样教的“可能性”是数学课吗?
笔者所倡导的魅力数学教育观认为:数学课要有数学味——思想的味道、思维的味道和思考的味道。概率课要有概率的味道,如何才能让“可能性”这一课上出概率的味道呢?《义务教育数学课程标准( 2011年版)》在内容标准中对这部分知识的教学提出了“在具体情境中,通过实例感受简单的随机现象,能列出简单的随机现象中所有可能发生的结果,能对一些简单的随机现象发生的可能性大小作出定性描述”的明确要求。下面,结合课程标准提出的教学要求,从课程标准的“四基”的角度分析“可能性”这节课究竟应该教什么、怎么教、为什么。
一、从基础知识的角度分析
基础知识在教学目标中属于结果目标,“可能性”这一课的基础知识究竟是什么?这是一个关键性的问题,有的教师把这节课的知识点定在“一定”“不可能”“可能”这三个词,这就不奇怪很多教师都反映这节课“教”和“不教”一个样,主要原因就在这里:“一定”“不可能”“可能”这三个词确实不需要“教”,因为学生早在生活中就学会了。那么,“可能性”一课从知识的角度上看究竟应该教什么?课程标准提出“在具体情境中,通过实例感受简单的随机现象”的目标要求。笔者认为:“可能性”这节课应该教的知识点不是“一定”“不可能”“可能”这三个词,而是“随机现象”。随机现象包含两层含义,一是在个别试验中呈现出不确定性:二是在大量重复试验中其结果又具有一定的规律性。因此,“随机现象的不确定性”是本节课的具体知识点,应该达到第一水平层次的要求“了解”,作為教学目标可以表述为“了解简单随机现象的不确定性”。
明确了“可能性”一课的基础知识应该教什么,下面接着探讨该怎么教、为什么。从随机现象的数学本质进行分析,一是随机现象要求可能发生的事件至少要有2种,二是随机现象要求随机试验能重复进行,因此,“抛硬币”是一个极佳的模型。然而,如何让学生了解随机现象的不确定性?笔者认为:倘若仅仅把“抛硬币”当成一个游戏活动,学生简单地“猜一猜”“抛一抛”“说一说”是无法达到预定教学目标的。教师可以在“抛硬币”之前先设计一个确定性的活动,再组织“抛硬币”的活动,从“确定的”过渡到“不确定的”,让学生形成对比。在“抛硬币”的试验中,不要让学生“猜一猜”——猜硬币落地后哪一面朝上,而应该让学生“想一想”——想让硬币落地后哪一面朝上。“猜一猜”容易让学生沉迷于游戏活动之中,“想一想”更能让学生体会到“我们无法主观控制硬币落地后哪一面朝上”,这样设计更加接近随机现象不确定性的数学本质。
二、从基本技能的角度分析
基本技能在教学目标中属于结果目标,“可能性”这一课的基本技能究竟是什么?这是本节课的另一个关键性问题,有的教师把这节课的技能点放在用“一定”“不可能”“可能”这三个词说一件事情(或一句话)上,这就是多数教师反映这节课“教”和“不教”一个样的另一个根本原因。那么,从基本技能的角度分析“可能性”一课,究竟该教什么?课程标准提出“能列出简单的随机现象中所有可能发生的结果,能对一些简单的随机现象发生的可能性大小作出定性描述”的目标要求。笔者认为“可能性”一课的基本技能,应该包括以下两个方面的内容:一是说出简单随机现象中所有可能发生的结果(即有几种可能),需要达到结果目标的第三层次水平“能”(相当于“掌握”);二是定性描述简单随机现象发生的可能性大小,需要达到结果目标的第三层次水平“能”(相当于“掌握”)。因此,“可能性”一课在基本技能方面,作为教学目标可以具体表述为:能说出简单随机现象中所有可能发生的结果,能定性描述简单随机现象发生的可能性大小。
明确了“可能性”一课的“基本技能”应该教什么以后,就该讨论怎么教,以及为什么了。第一,在“抛硬币”活动中,不能让学生仅仅沉浸在游戏活动的欢乐之中,而应该让学生在每一次游戏活动之前先“想一想”,再“说一说”有几种可能发生的情况,以及为什么。第二,在概率知识的学习历程中,描述随机现象发生的可能性大小,需要经历一个从定性描述到定量描述的过程,定性描述是用“一定”“不可能”“可能”三个词语进行描述,定量描述是用“1”“0”“大于0小于1的分数”进行描述。“可能性”一课,要让学生学会用“一定”“不可能”“可能”定性描述随机现象发生的可能性大小,而不是让学生学会用这三个词说一件事(或一句话)。比如,在“抛硬币”活动中,不是让学生用“可能”描述这个游戏活动的全过程,说“硬币落地后可能正面朝上,也可能反面朝上”,而是应该让学生根据“抛硬币”的一个随机事件(如硬币落地后正好正面朝上),选择适当的描述性词语,描述这个随机事件发生的可能性大小(可能)。因此,教学时,教师可以先叙述随机现象中的一个随机事件,然后让学生定性描述这个随机事件发生的可能性大小,这才是本节课应该达到的技能目标要求。
三、从基本思想的角度分析
基本思想是数学课程标准的“四基”的重要内容,在教学目标中属于过程目标。数学思想是指数学知识、方法在更高层次上的抽象与概括,数学思想常常蕴涵在数学知识的形成、发展和应用过程中。一般认为,数学基本思想有抽象思想、推理思想和建模思想,抽象思想包括集合思想、分类思想、符号表示思想、对应思想、数形结合思想、变中不变思想、极限思想等;推理思想包括转化思想、归纳思想、类比思想、演绎思想等;建模思想包括简化思想、量化思想、优化思想、函数思想、方程思想、随机思想、统计思想等。“可能性”一课蕴涵的数学思想主要有随机思想和变中不变思想——应该达到过程目标的第二层次水平,教学目标可以表述为“体会随机思想和变中不变思想”。
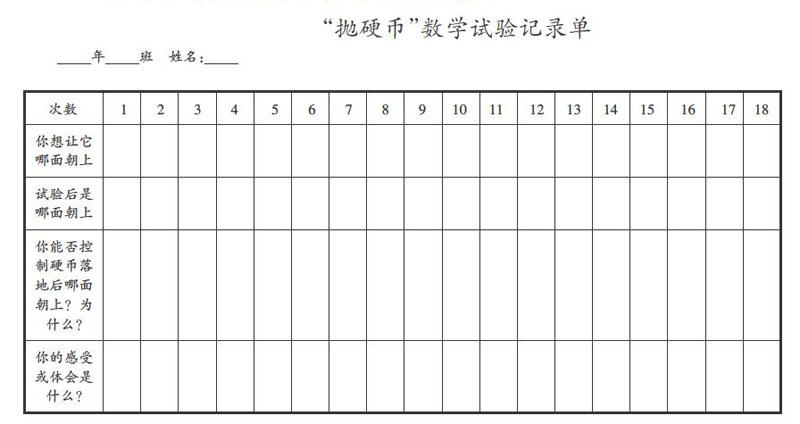
如何在“可能性”一课中融人数学思想的教学,让学生在数学活动中体会随机思想和变中不变思想?在“抛硬币”这一随机试验中可以设计一张试验记录单(如下图所示),第一栏为“你想让它哪面朝上”,第二欄为“试验后是哪面朝上”,要求学生每次试验之前先填写第一栏,试验后再填写第二栏,试验18次后,看一看记录单,想一想:能否控制硬币落地后哪面朝上?为什么?在抛硬币这个试验中,什么变了?什么不变?融人数学思想的教学,关键在于教师的活动设计和语言启发,以及及时引导学生进行必要的数学思考。在“抛硬币”的数学试验中,通过巧妙设计的记录单,学生体会到随机事件具有不确定性,且无法人为控制硬币落地后是哪面朝上。在这个过程中让学生体会随机思想:每一次试验是哪一面朝上是不确定的——“变”,然而所有发生的情况只有2种是确定的——“不变”,这是变中不变思想。
四、从基本活动经验的角度分析
基本活动经验是数学课程标准的“四基”的重要内容,在教学目标中也属于过程目标。活动经验是学生经历数学活动过程的一种结果,是学生在“做”的过程和“思考”的过程中逐步积淀的,是学生在数学学习活动过程中逐步积累的,积累数学活动经验是提高学生数学素养的重要标志。因此,帮助学生不断积累基本活动经验是数学教学的重要目标,主要包括观察的经验、操作的经验和思维的经验,基本活动经验属于过程目标的教学要求,应该达到第一层次水平,作为教学目标可以表述为:积累数学活动经验。
“抛硬币”在“可能性”一课中是一个简单随机现象的基本模型,是让学生在试验活动中积累数学活动经验的重要载体。教师在组织“抛硬币”试验活动时,不能让学生将其当成游戏来玩耍,而应该正确引导学生进行必要的观察、操作和思考,不断帮助学生积累经验,为后续概率知识的学习奠定重要的经验基础。
综上所述,“可能性”是小学概率知识的起始课,它是一节“种子课”,让学生了解简单随机现象的不确定性,能说出简单随机现象中所有可能发生的结果,能定性描述简单随机现象发生的可能性大小,体会随机思想和变中不变思想,积累基本活动经验,从此开启随机现象的学习和研究之旅。这才是一节有概率味道的数学课。
(责编金铃)
