关于梯形有关概念教材编写及二次开发研究(一)
2020-07-07刘慧
刘慧


[摘要]現行教材中关于梯形有关概念的编写,一是概念探索活动的设计缺乏从生活中探究、抽象、提炼出概念的过程,致使思维含量很低;二是有的概念表述不严谨或存在科学性错误;三是梯形上下底概念界定不明确导致理解的混乱。分析认为,这与对“淡化概念”教学理解的偏颇,致使教学中“形式”与“实质”全面淡化不无关系。
[关键词]教材编写;梯形;高;上底;下底
[中图分类号]
G623.5
[文献标识码]A
[文章编号] 1007-9068( 2020) 20-0001-06
梯形是学生在小学第二学段学习的基本图形之一。关于梯形的有关概念,国内各版本教材安排的时间有所不同:人教版教材安排在四年级第一学期;沪教版教材安排在五年级第一学期;北师大版教材把梯形的概念安排在四年级第一学期,而把梯形的上下底和高安排在五年级第一学期;其他版本教材都是安排在四年级第二学期。由于梯形在生活中有着非常广泛的应用,且内容比较简单,各版本教材在编写时都较充分地体现了新课改的教育理念,注重与生活的联系和探索活动的设计。然而,研读、分析教材的编写以及教学实证后发现,教材编写存在着一些不足,有必要对其进行二次开发。本研究在分析了教材对于梯形有关概念的编写存在不足的基础上,对教材进行了二次开发,并进行教学实践且取得了良好的效果。
一、梯形概念探索活动的比较分析
综观各版本教材,关于梯形概念探索活动的设计虽然大同小异,但从外在形式来看可分为三种情况。
1.“图形一概念一图形”的设计
诸多教材中,直接从图形人手探讨梯形概念的只有北师大版教材(如图1)。它是通过对四边形进行分类,引导学生观察、对比后发现梯形的特征,提炼出概念,再找出梯形的图形。这是单纯从图形到图形的设计,前后都没有联系生活,学生不能从生活当中体会到学习的必要性,也看不到在生活中的应用。值得肯定的是,通过对比四边形,学生可能较容易发现梯形的特征。
2.“构造图形一概念一生活”的设计
有些教材是让学生先通过操作活动构造几个梯形图形,再归纳图形的特征,进而得出梯形的概念,而后找一找生活中的梯形。如,沪教版教材(如图2)和浙教版教材(如图3)的设计。这体现了让学生动手动脑进行探索的先进教育理念,也体现了数学知识的应用。虽然两者的构造方法不同,但教材都是直接给出“图形的一组对边平行,另一组对边不平行”,学生不用思考与探讨就能获得梯形的特征,思维含量很低。另外,联系生活也仅仅是说明了生活中有梯形这种图形而已。
3.“生活一图形一概念”的设计
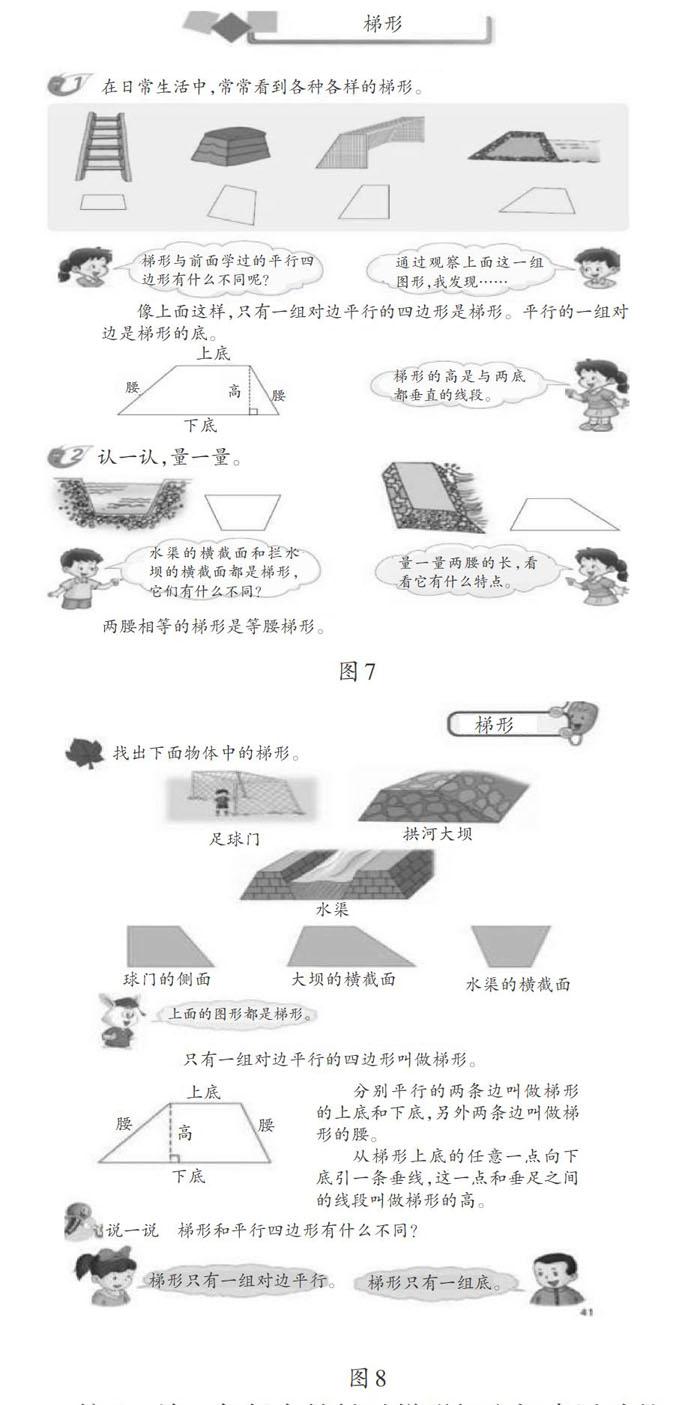
有些教材是从生活中常见的实物(如梯子、跳箱、足球门、河坝、房顶、画架、篮球场等)图片人手,让学生发现其中含有一些梯形,再引导学生探讨梯形的特征,提炼出有关概念。这样编写的教材有人教版教材(如图4)、苏教版教材(如图5)、青岛版教材(如图6-1和图6-2)、西师大版教材(如图7)、冀教版教材(如图8)。这种设计能让学生体验到数学知识来源于生活,体会到知识的应用价值。从另一个角度来看,教材中呈现的屋顶、水渠和河坝横截面等严重脱离小学生的生活,要让他们想象出来很困难;再者,教材也只是告诉学生生活中有梯形而已,这还是从图形来探讨梯形的概念。
综上可知,各版本教材对梯形概念探索活动的设计实质上都是从图形到图形,即使联系生活也是浮于表面,流于形式,思维含量很低。因为设计没有真正触及生活,没有从生活中抽象、提炼出“这种图形为什么叫梯形”“为什么只有一组对边平行,而另一组对边不平行”“为什么上底比下底短”“生活中的很多事物为什么要设计成这种形状”等相关知识。实际上,这些都能让学生从生活中探索、抽象、提炼出来(详见研究(二)),进而真正理解梯形的有关概念,体会到知识的广泛应用,做到终身不忘。
二、有的概念表述缺乏严谨性或存在科学性错误
众所周知,数学中的概念是学生学习其他数学知识与进行思维的起点和基础。正确理解数学概念是学生掌握数学知识,进行科学思维,发展数学能力的前提。但是,一些教材对概念表述缺乏严谨性,甚至存在科学性错误,主要表现在以下方面。
1.对梯形的高的表述缺乏严谨性或存在错误
西师大版教材将梯形的高表述为“梯形的高是与两底都垂直的线段”(如图7)。显然,这表述相当不严谨。众所周知,梯形的高是夹在两底间的垂线段,并不是与两底都垂直的线段就是高。北师大版教材在五年级上册一次性就给出了三角形、平行四边形和梯形的高。首先,给出了“从一个顶点向底引出的、与底垂直的线段就是高”(如图9)。这不仅犯了与西师大版教材同样的错误,而且“从一个顶点”的前提对平行四边形和梯形的高来说存在局限性,束缚了学生的思维。也许编者认识到了存在的问题,于是又给出了“平行四边形可以从边上任意一点向对边画垂线,画出的这些线段都是高”。这仅仅补充了对平行四边形的高的定义,还是没说清画垂线画到哪里为止。
若按上述教材的定义,一个梯形(包括三角形和平行四边形)的高的长度就可以是任意长度。虽然梯形有无数条高,但长度是相等的,不是有无数条长度不同的高,二者不能混淆,毋庸多言。
其次,以下教材中对梯形的高的表述本质是一样的,只是个别字词不同,但都存在问题。具体地说,浙教版教材(如图10)把梯形的高定义为“从梯形上底的一点向下底作一条垂线,这个点和垂足间的线段叫做梯形的高”。沪教版教材(如图2)把梯形的高定义为“从上底上一点向下底画垂线,这个点和垂足之间的线段叫做梯形的高”。冀教版教材(如图8)把梯形的高的定义为“从梯形上底的任意一点向下底引一条垂线,这一点和垂足之间的线段叫做梯形的高”。若根据这三个版本教材的定义,从梯形下底上一点向上底引一条垂线,这个点和垂足之间的线段就不是梯形的高了?显然,这些定义有失偏颇,且严重束缚了学生的思维。
2.四边形的概念表述错误
虽然四边形的概念不属于梯形的教学内容,但梯形是四边形。然而浙教版教材(如图3)一开始就给出:“画出与下面各组平行線相交的2条不平行直线,构成一些四边形。构成的图形是哪一类四边形?”这样的四条直线构成的图形是四边形?浙教版教材第80页“平行四边形的边与角”一节存在同样的问题:“在一组平行线上,画出另一组与它们相交的平行线,构成四边形。这些四边形有什么特点?”(如图11)由此可见,这些表述不是失误或印刷错误造成的,是严重的科学性错误。众所周知,上述描述中构成的图形不是四边形,而是《高等几何》(射影几何)中的简单四线形,《数学辞海》也将其称为简单四线形。只能说这样构成的图形中有四边形,或图形的一部分是四边形。再者,教材给出的图形与由四条不共线的线段首尾依次相接围成的(凸)封闭图形——四边形,是一样的图形吗?
当然,上述教材中概念不严谨或存在错误的问题,可能是考虑到小学生的接受能力,为了体现“淡化概念”的教育理念而精心设计的。可是,其他版本教材给出的严谨、科学的定义,难道学生就接受不了吗?这个问题值得我们数学教育工作者深思。
三、梯形上下底界定的不明确导致理解混乱
关于梯形上底和下底的概念,所有教材中都没有给出明确的界定。有的教材连底的定义都没有给出,只是在图形中标出了上底、下底,如人教版教材(如图4)、青岛版教材(如图12)、北师大版教材(如图9);其他教材(如图2、图3、图7、图8),以及图13都给出了类似的定义:互相平行的一组对边分别叫做梯形的上底和下底。可到底哪条是上底,哪条是下底均没有明确界定,仅仅是在图中标了出来。最重要的是,所有教材中标出上下底的梯形都是将上下底水平(横着)放置,且上面的底比下面的底短。
这样一来就导致学生对上底和下底的理解产生混乱:到底在上边的叫上底,还是短的叫上底?如果上下底不是水平放置的梯形呢?如果上下底是水平放置的梯形,但短的底在下,长的底在上,又怎么办呢?这不仅给学生造成了困惑,还让不少教师也感到困惑。笔者于2019年7月7日6:05上百度搜索“梯形的上底和下底怎么区分?”得到了“百度为您找到相关结果约9,290,000个”的结果,可见不少人处于困惑之中。拥有4亿用户的“100作业帮( https://www.zybang.com/question/f443f3e088199da30ac4lcba257ecf53html)给出了一个教师与教研组讨论及查资料后的“优质解答”,主要内容如下:
关于梯形上下底的界定……,大致有以下观点:一、不论位置上或下,其中较短的一条叫上底,较长的一条叫下底;二、不管它的长短,位置在上的叫上底,位置在下的叫下底。三、如果梯形是横着放的,平行的一组对边,上面的叫上底,下面的叫下底;如果梯形是竖着放的,平行的一组对边画有高时,有垂直符号的称下底,另一条称上底。陕西人民教育出版社出版的《小学教材全解》101页写道:“梯形中互相平行的一组对边中,通常把上边叫做梯形的上底,下边叫做梯形的下底。”人民教育出版社出版的《教师教学用书》93页提到:“要注意说明,通常把较短的底叫上底,较长的底叫下底。”疑惑中,个人还是比较支持第一种观点,因为如果以方位定上下底(即上面的为上底,下面的为下底),那“竖放的梯形”也就是说梯形的两底在侧面,叫它上、下底也不恰当……其实,梯形的上下底之争完全不必太较真,即使人教版的教学用书也只是用了“通常”二字,就是习惯上,没什么科学道理的,也是相对而言的,无论怎样区分都不影响梯形的特性。我想这大约也是为什么教科书没有给出明确定义的原因吧……
对于梯形上下底的理解处于一片混乱状态之中,不仅导致教师教学模棱两可或回避不谈,学生更是稀里糊涂,家长指导学生完成家庭作业时也一筹莫展。
关于梯形的上下底是不是没有明确的界定?其实,《数学辞海》在“梯形”条目中明确定义:“通常把短的称为上底,长的称为下底。”再者,在不同版本的《教师教学用书》中,有的提出了类似的教学建议,有的避而不谈。既然有明确界定,那为什么各版本教材中都不说明呢?是为了“淡化概念”,还是和上面那位教师一样,认为“通常”二字就是习惯,没有科学道理?抑或是当梯形的上下底不水平放置(横放),或水平放置(横放)时长的底在上面,上下的方位与感觉不相符或矛盾,不好解释,也解释不通?抑或是不管上底下底,只要不影响梯形面积的计算就行了?
其实,梯形的上下底界定为“短的是上底,长的是下底”是具有科学性的,也没必要加“通常”二字,因为它来源于人们的现实生活,是对事物抽象的结果(详见研究(二)),不是随意而为的。
四、原因分析
众所周知,数学概念是整个数学大厦的奠基石,它对学生学习数学的重要性毋庸置疑。若说概念探讨流于形式还尚无大碍,但概念表述的科学性是必须保证的。当然,由于数学的严谨性和抽象性等特征,再加上小学生认知特征的制约,小学教材不可能建立在严格的理论体系之上,用通俗易懂的、生活化的语言对数学概念进行宏观描述是可以的,也是必要的。但是,这些不能成为教材中概念表述不严谨,甚至存在科学性错误,或回避概念的理由。
回顾课程改革的历程,基于学生学习数学困难和减负的需要,“淡化概念”教学成为一种“理念”和时尚,课程标准也降低了对数学概念教学的要求。笔者于2019年7月6日8:10在百度搜索“淡化概念教学”,得到“百度为您找到相关结果约3,190,000个”的结果,且绝大多数文章都提出要淡化概念教学,只有极个别的文章提出异议。研读一些专家的有关论述,发现“淡化概念”主要有以下观点:一是不要求学生死记硬背,不出单纯考数学概念的题;二是淡化文字叙述,甚至可以不叙述,让学生了解其大意就行;三是教学不要在概念上下过多的功夫。当然,也指出“淡化概念”教学是“淡化形式”,目的是“注重实质”“讲究实效”,让学生在“用”和“做”中更好地领悟与理解概念。事实上,“淡化概念”的观点很难实现,甚至存在矛盾。试问:淡化文字叙述,学生只了解概念的大意就能认识到概念的实质?就能更好地理解概念?心理学理论早已表明,实现数学语言和汉语言的转换是促进学生内化与理解数学知识的关键。由此,概念不表述何以进行内化与理解?
