缺项3×3阶上三角算子矩阵的可能点谱
2020-07-07吴秀峰黄俊杰
吴秀峰, 黄俊杰
(1.内蒙古师范大学数学科学学院,内蒙古呼和浩特010022;2.内蒙古大学数学科学学院,内蒙古呼和浩特010021)
§1 引 言
缺少了某些元素的算子矩阵称为缺项算子矩阵.算子矩阵的谱补问题旨在讨论缺项算子矩阵中所缺的元素对整个算子矩阵谱的影响,在插值理论,换位提升理论,以及系统控制理论中具有重要应用.缺项算子矩阵的谱补问题有两个基本内容:一是缺项算子矩阵的谱扰动,即当所缺的元素跑遍特定集合时所得算子矩阵的谱的交集,它是整个算子矩阵谱的稳定的组成部分;二是缺项算子矩阵的可能谱,即当所缺的元素属于特定集合时所得算子矩阵的谱的并集,它反映了整个算子矩阵的谱的分布范围.
设H1,H2,H3,H均为无穷维复可分Hilbert空间.以B(Hi,Hj)表示从Hi到Hj的所有有界线性算子构成的集合,特别地,B(Hi)表示Hi上的所有有界线性算子构成的集合,其中

给定算子A∈B(H1),B∈B(H2),C∈B(H3),记
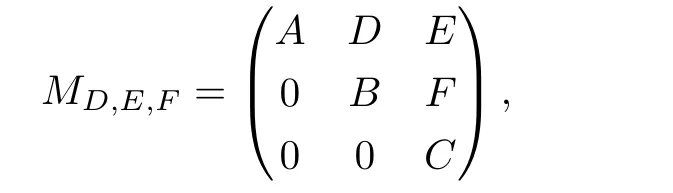
其中D∈B(H2,H1),E∈B(H3,H1),F∈B(H3,H2)为缺项的算子,则称MD,E,F为H1⊕H2⊕H3上的3×3阶缺项上三角算子矩阵.类似可有对给定算子A∈B(H1),B∈B(H2),记2×2阶缺项上三角算子矩阵
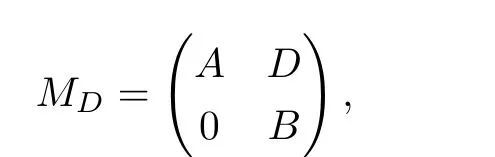
其中D∈B(H2,H1)为缺项的算子.
经过近二十年的积累,2×2阶上三角算子矩阵的谱补问题研究已日臻完善,涌现出诸如谱,近似点谱,亏谱,本质谱,Weyl谱,Browder谱,点谱,剩余谱以及连续谱等的补问题结果[1-9].对于缺项3×3阶上三角算子矩阵,文[10]描述了左(右)Fredholm谱扰动以及Weyl型定理;文[11]研究了Moore-Penrose谱扰动;文[12]和[13]分别给出了点谱,剩余谱和连续谱的可能谱和扰动的描述.文[14]研究了谱扰动以及填洞问题.此外,文[15]研究了四类点谱的扰动,文[16]研究了1,2类点谱和1,2类剩余谱的可能谱.本文继续研究缺项3×3阶上三角算子矩阵的谱补问题,得到四类点谱的可能谱.需要指出的是:缺项3×3阶算子矩阵的某些结论不能由2×2阶情形直接推出,不是其简单推广;文中对于点谱的分划可参见[17],谱的这种细分划对于讨论算子矩阵的半群生成定理,谱包含性质等具有一定的作用[18-19].
下面给出一些基本概念和辅助引理.对于算子T,分别以T∗,N(T),R(T)表示T的共轭算子,零空间和值域,记n(T)=dimN(T),d(T)=dimN(T∗).
定义1.1设X为Banach空间,T是X中的有界线性算子.称集合
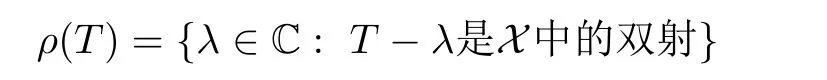
为T的预解集,预解集ρ(T)中的元素λ称为T的正则值.称集合σ(T)=Cρ(T)为T的谱.易知,T的谱σ(T)可分成互不相交的3个组成部分:
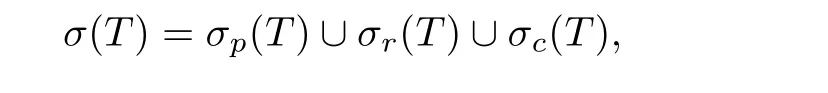
其中集合

分别为T的点谱,剩余谱和连续谱.此外,称集合

分别为T的左谱,右谱,Moore-Penrose谱,压缩谱,并且为叙述方便记记ρin(T)=Cσp(T),ρ∗(T)=Cσ∗(T),其中σ∗(T)∈{σl,σδ,σm,σco},ρ∗(T)∈{ρl,ρδ,ρm,ρco}. 如所熟知,λ∈σm(T)当且仅当R(T−λ)不闭;λ∈ρl(T)当且仅当T−λ为具有闭值域的单射.类似于文[17],对点谱进一步细分为
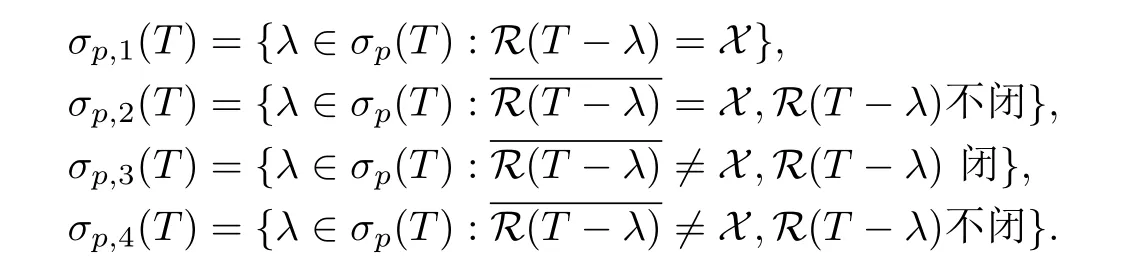
定义1.2设A∈B(H1),B∈B(H2),C∈B(H3)为给定算子,称
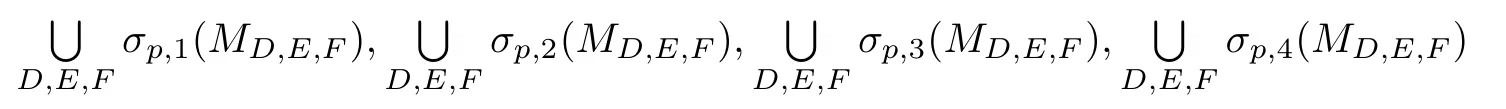
分别为缺项算子矩阵MD,E,F的1类可能点谱,2类可能点谱,3类可能点谱,4类可能点谱.

§2 主要结果及证明



不难看出λ∈σp,2(MD,E,F).若λ∈∆43,则定义E=0且F形如(1),

易得λ∈σp,2(MD,E,F).
情形1λ∈σco(C)∪(ρin(A)∩ρin(B)∩ρin(C)).此时显然任给D,E,F均有λ∈σco(MD,E,F)或者λ∈ρin(MD,E,F),从而λ/∈∆.
情形2λ∈ρδ(C)且d(B−λ)>n(C−λ).此时对任意D,E,F算子矩阵MD,E,F−λ均有形如(3)的分块形式,其中(C−λ)1为为可逆算子.注意到d(B−λ)>n(C−λ),易知无论如何选取算子D,E,F均有R(F22)不稠密,从而λ∈σco(MD,E,F).因此λ/∈∆.
情形3λ∈ρδ(C)∩ρm(B)且d(A−λ)+d(B−λ)>n(B−λ)+n(C−λ).此时由定理2.1的情形5可知,对任意D,E,F均有λ∈σco(MD,E,F).因此λ/∈∆.
情形4λ ∈ ρm(A)∩ρm(B)∩ρδ(C)且min{n(B−λ),d(A−λ)}<∞,min{n(C−λ),d(A−λ)}<∞且min{n(C−λ),d(B−λ)}<∞.此时任给D,E,F算子矩阵MD,E,F−λ均有如下分块表示

其中(A−λ)1,(B−λ)1,(C−λ)1均为可逆算子.因此,存在可逆算子U和V使得
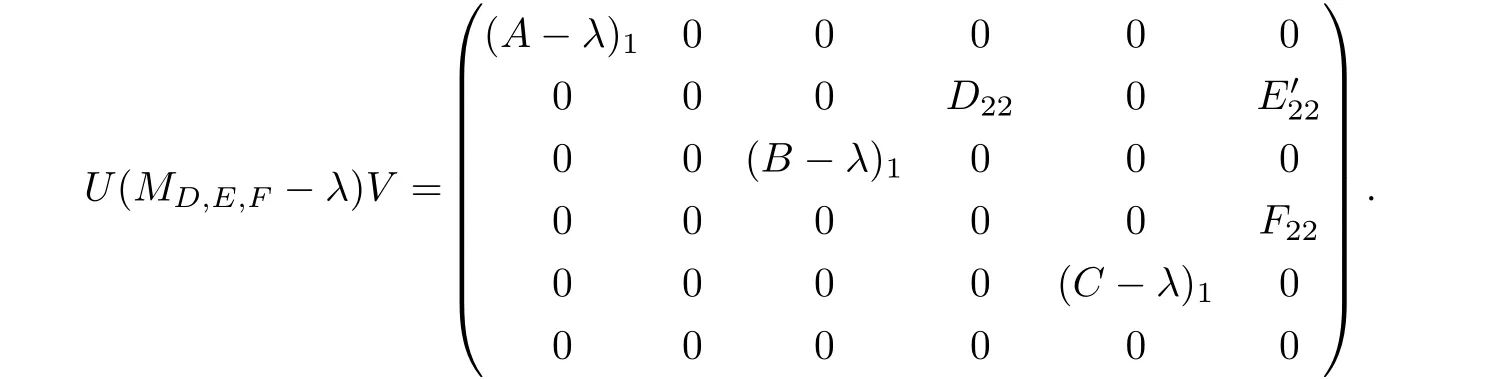
定理2.3设A∈B(H1),B∈B(H2),C∈B(H3)为给定算子,则
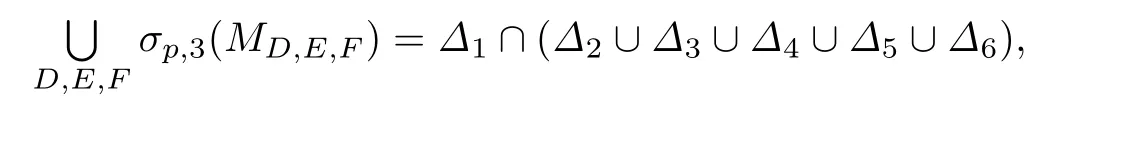
其中

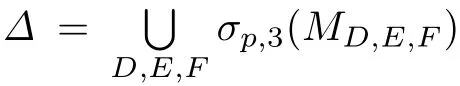
(1)设λ∈∆1∩∆2.定义算子D=0,E=0,F=0便得λ∈σp,3(MD,E,F).
(2)设λ∈∆1∩∆3.因为λ∈σm(A)∩σm(B)∩σm(C),所以dimN(A−λ)⊥=dimN(B−λ)⊥=dimN(C−λ)⊥=∞.若n(B−λ)=d(A−λ)=∞,则定义E=0且
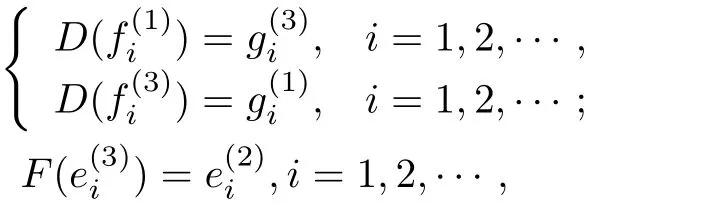
容易验证λ∈σp,3(MD,E,F).类似地可以证明当d(B−λ)=n(C−λ)=∞或者n(C−λ)=d(A−λ)=∞时,存在D,E,F使得λ∈σp,3(MD,E,F).
(3)设λ∈∆1∩∆4.现设λ∈∆41.若n(B−λ)=∞,则定义E=0,F=0且
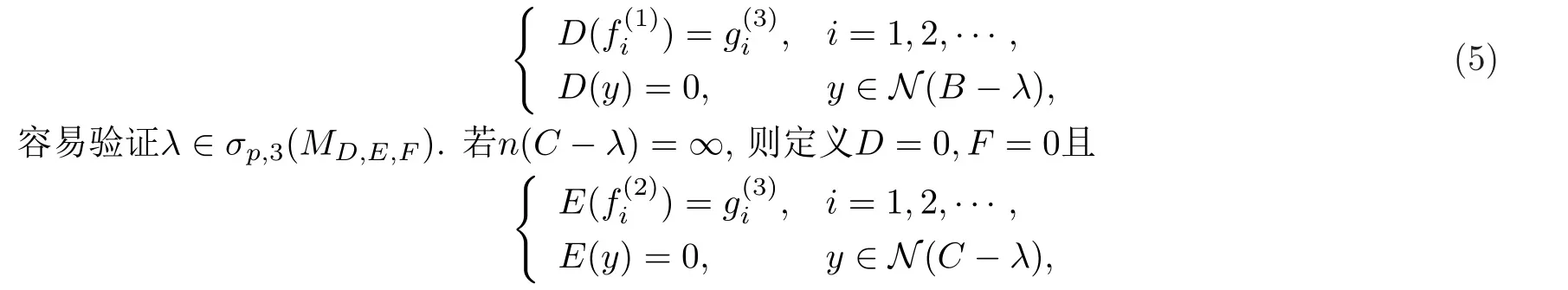
易得λ∈σp,3(MD,E,F).类似地可以证明当λ∈∆42∪∆43时,存在D,E,F使得λ∈σp,3(MD,E,F).
(4)设λ∈∆1∩∆5.现设λ∈∆51.若n(C−λ)=∞,则定义D=0且

容易验证λ∈σp,3(MD,E,F).若n(B−λ)=d(A−λ)=∞,则取(2)中的D,E,F,从而λ∈σp,3(MD,E,F).类似地可以证明当λ∈∆52时,存在D,E,F使得λ∈σp,3(MD,E,F).


