几类非线性数学物理方程精确解的符号计算
2020-07-07马立媛沈守枫
周 凯, 杨 军, 马立媛, 沈守枫
(1.浙江工业大学应用数学系,浙江杭州310023;2.上海交通大学数学系,上海200240)
§1 引 言
孤子理论的发展说明了构造非线性数学物理方程精确解的重要性.例如,钟型和扭结型孤子解可以用来分析和模拟流体,等离子体和弹性介质中的波现象.近些年,由于符号计算软件Mathematica,Maple和Matlab的完善,一系列数学机械化方法如Hirota双线性方法,函数展开法,Painlev´e分析和Lie对称方法得到了快速发展[1-13].
首先利用Hrota双线性方法[14-16]考虑如下的可积非局部离散mKdV方程.
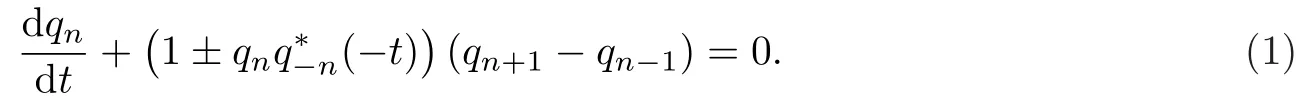
这里t∈R是连续变量,n∈N是离散变量,∗表示复共轭.方程(1)拥有离散的矩阵谱问题
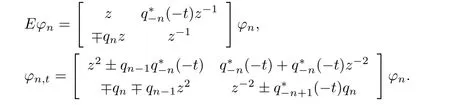
移位算子E定义为Ef(n)=f(n+1),Ef(−n)=f(−(n+1)).方程(1)可退化为非局部mKdV方程[17-18]
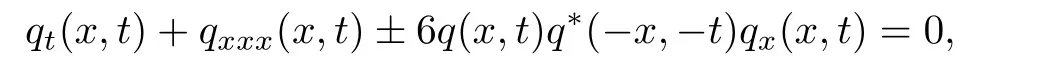
其次,利用Jacobi椭圆函数直接构造如下的多分量Klein-Gordon方程
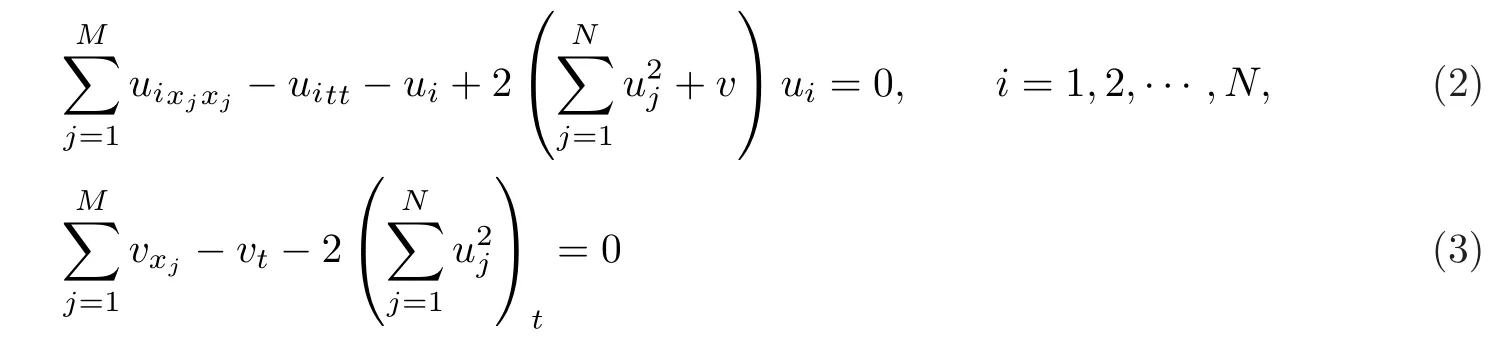
和多分量长波-短波方程
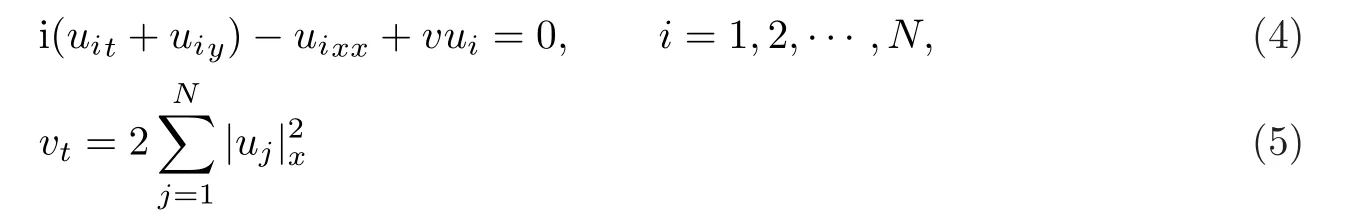
的精确解.事实上,对于多分量方程来说,很少有其精确解成功构造的工作.各种形式的Klein-Gordon方程可以用来研究浅水波,光纤通讯和量子物理[19-24].特别地,当M=1时,文献[25]给出了Painlev´e分析.对于长波-短波方程,文献[26]利用Hirota双线性方法给出了线孤子解.
文章的安排如下:利用Hirota双线性方法,§2给出了方程(1)的N-孤子解的显式表达式.特别地,分析了2-孤子解的渐近行为.§3利用Jacobi椭圆函数展开法给出了方程(2)-(3)和方程(4)-(5)的行波解.§4是文章的结论.
§2 方程(1)的2-孤子解和渐近行为
考虑到1-孤子解的表达式较为简单,将以注记的形式给出,所以直接构造2-孤子解.首先引入Hirota双线性算子


这里双线性算子A1和A2由

及
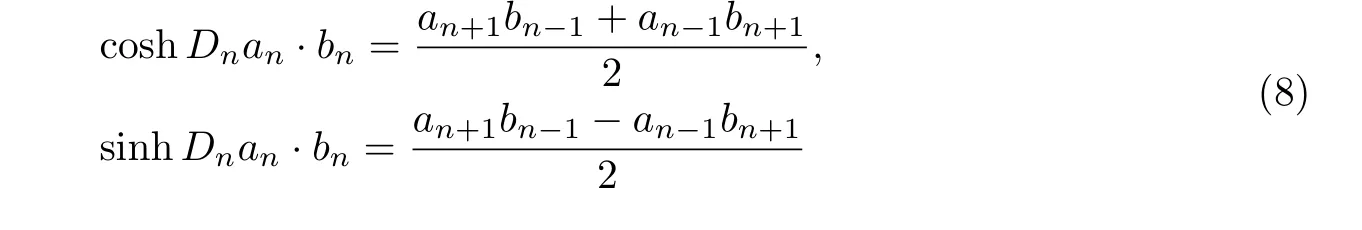
给出.

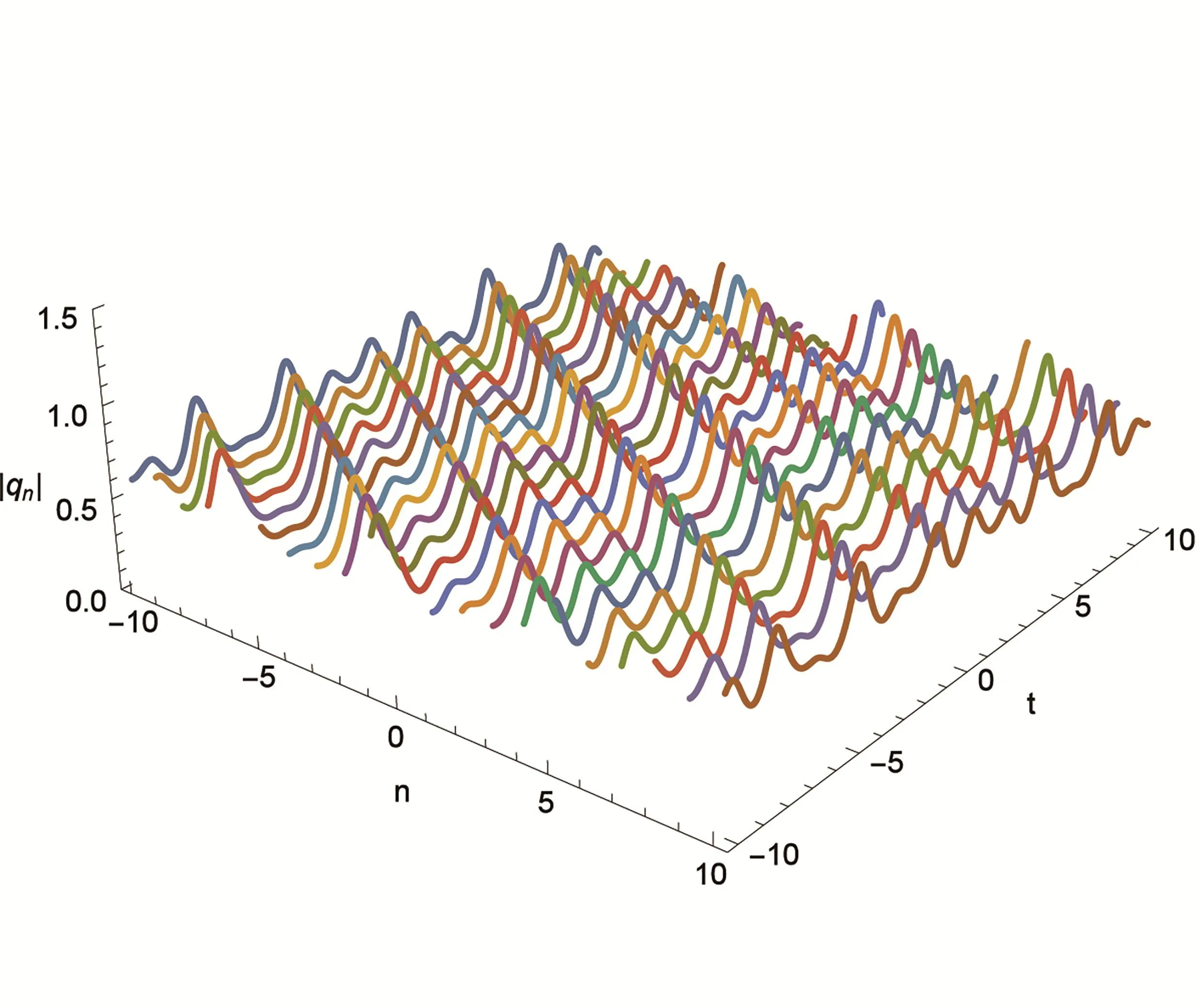
图1 参数取k1=3i,k2=2i的2-孤子解

图2 参数取k1=0.2+i,k2=i的2-孤子解
进而对于其它方程,可知恒成立.
最后令ε=1,2-孤子解为
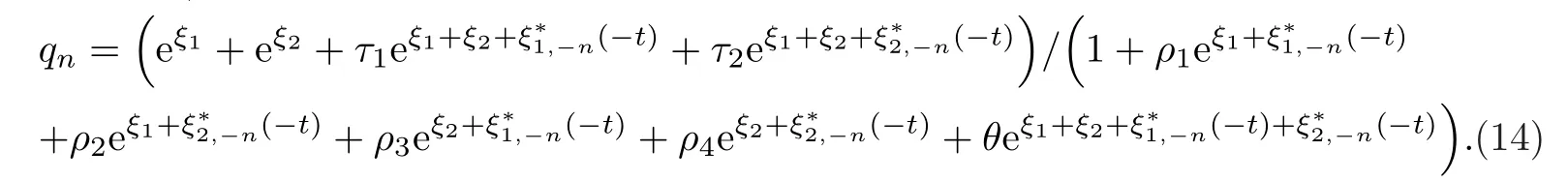
简便起见,这里记τ1=a(1,2,1∗),τ2=a(1,2,2∗),ρ1=a(1,1∗),ρ2=a(1,2∗),ρ3=a(2,1∗),ρ4=a(2,2∗),ρ5=a(1,2)和θ=a(1,2,1∗,2∗). 当

该2-孤子解(14)表现为保持弹性碰撞的周期孤子,见图1.
如果选择

则2-孤子解(14)的动力学行为见图2.
当固定ξ1,可得
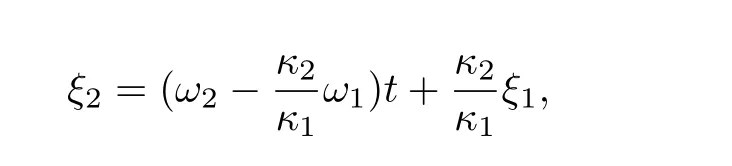


利用符号计算软件Maple,可以构造该精确解的相互作用行为.
§3 方程(2)-(3)的Jacobi椭圆函数解
设方程(2)-(3)的行波解为如下形式,

分别是模为m∈(0,1)的Jacobi椭圆正弦函数,Jacobi椭圆余弦函数和第三类Jacobi椭圆函数.这些Jacobi椭圆函数有如下的平方关系式
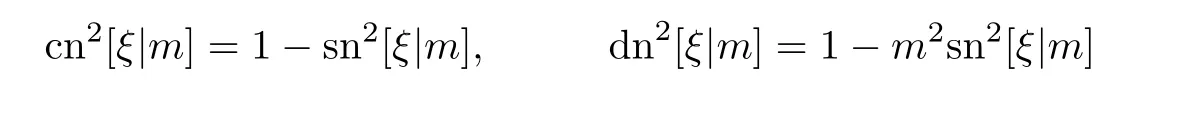
和导数关系式

这样可以分三种情形直接求解方程:
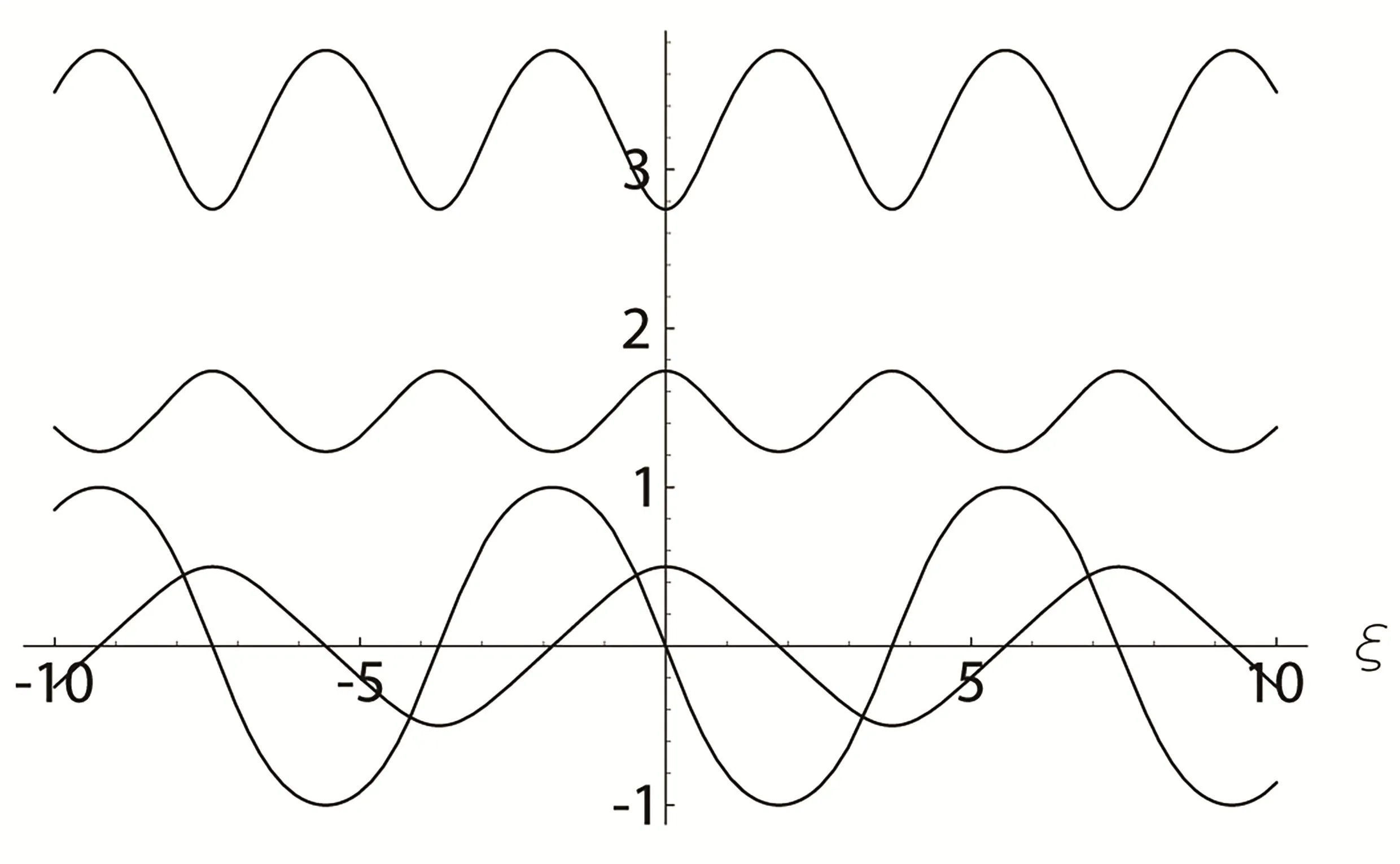
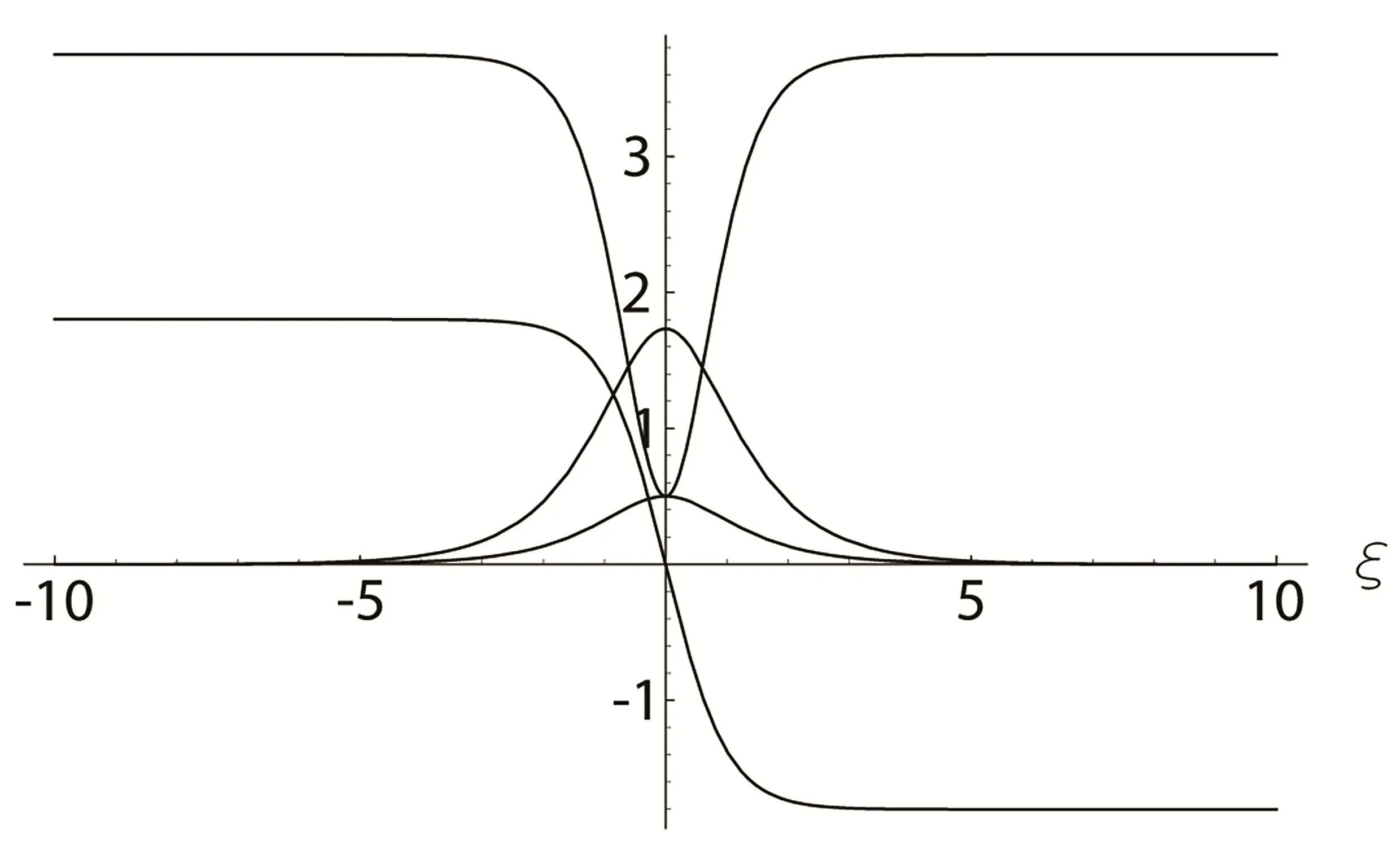
情形1当0 图3 3-耦合方程的Jacobi椭圆函数解 也就是说,构造了方程(2)-(3)新的精确解: 这里条件0 并且需要满足式子(28).当模m→1,上述精确解退化为相应的双曲函数解,即1-孤子解. 情形2当p=N时,类似可得另一个新的行波解 图4 3-耦合方程相应的1-孤子解 且需要满足如下式子: 情形3当p=0,q=N时,可得如下新的行波解 另外令dn[mξ|m−1]=cn[ξ|m],情形p=q=0 注3.1对于多分量长波-短波方程(4)-(5),令 类似于上述计算过程,可得新的精确解(29)-(30),其系数为 且需要满足如下的约束条件 非局部方程有其自身特殊的性质和应用,已经引起专家学者的极大关注.例如非局部mKdV方程是一个可积的无穷维哈密顿系统,其作为一个重要的数学模型能很好描述非线性时空对称介质中的波传导现象.典型的非局部方程包括非局部非线性Schr¨odinger方程,非局部离散非线性Schr¨odinger方程[27-36],非局部KdV方程,非局部mKdV方程[37-38]和非局部Davey-Stewartson方程[39-40].非局部离散mKdV方程是一个新的可积系统.在§2中,利用Hirota双线性方法,构造了该方程的1-孤子解,2-孤子解和N-孤子解,并给出了2-孤子解的渐近分析. 对于多分量Klein-Gordon方程和多分量长波-短波方程,直接构造了新的Jacobi椭圆函数解.当模m→1时,这些解退化为相应的双曲函数解.最后,这些方程的其它的数学物理性质如Painlev´e性质,Lie对称有待进一步研究.
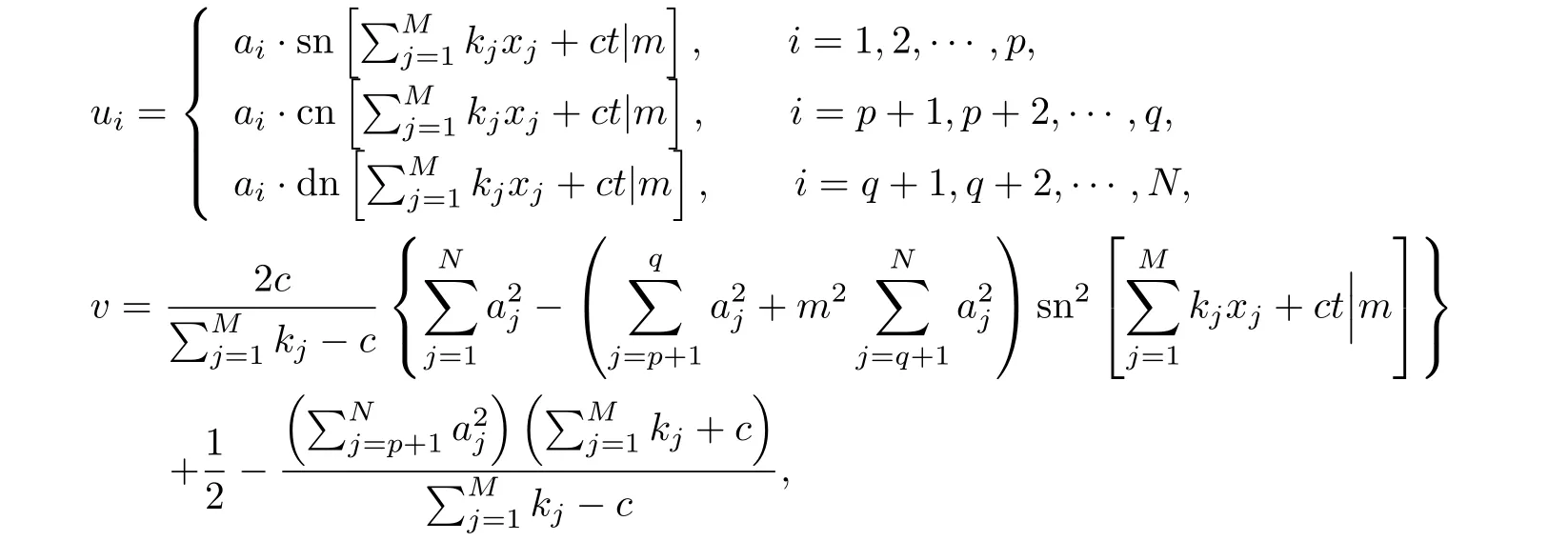


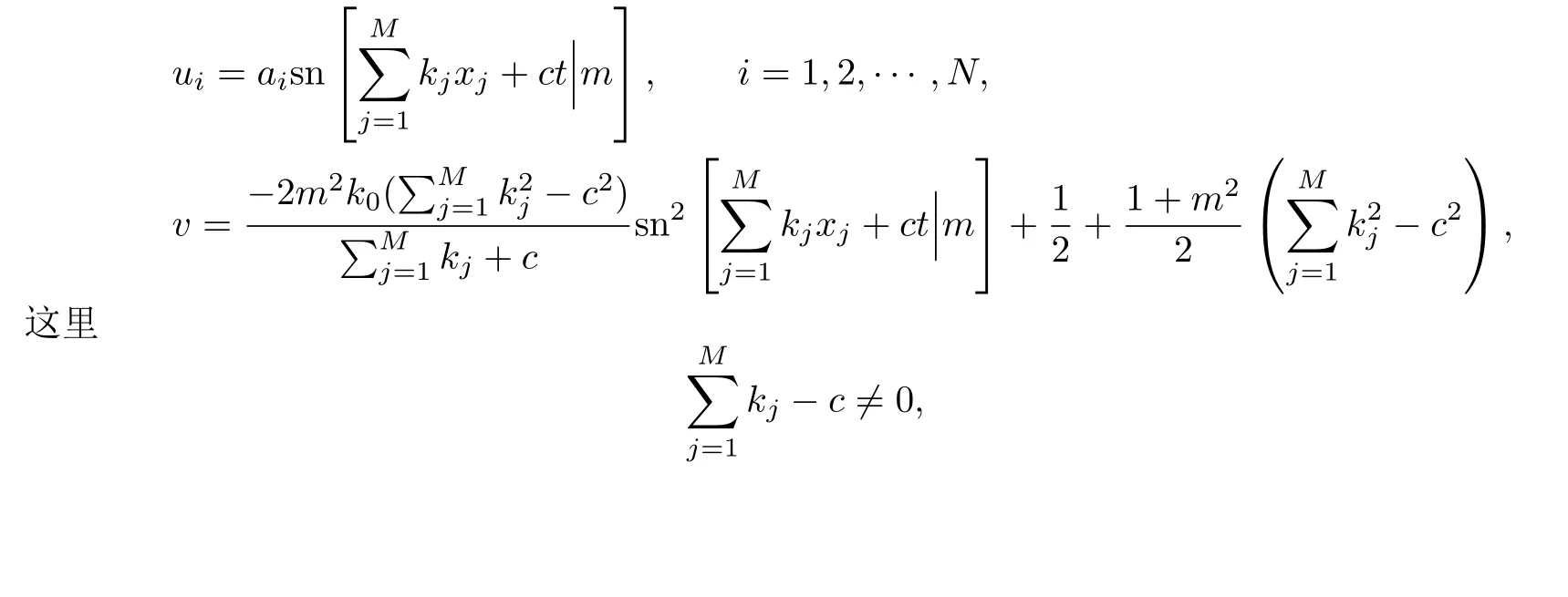
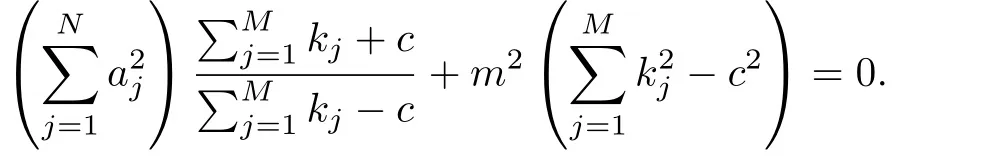
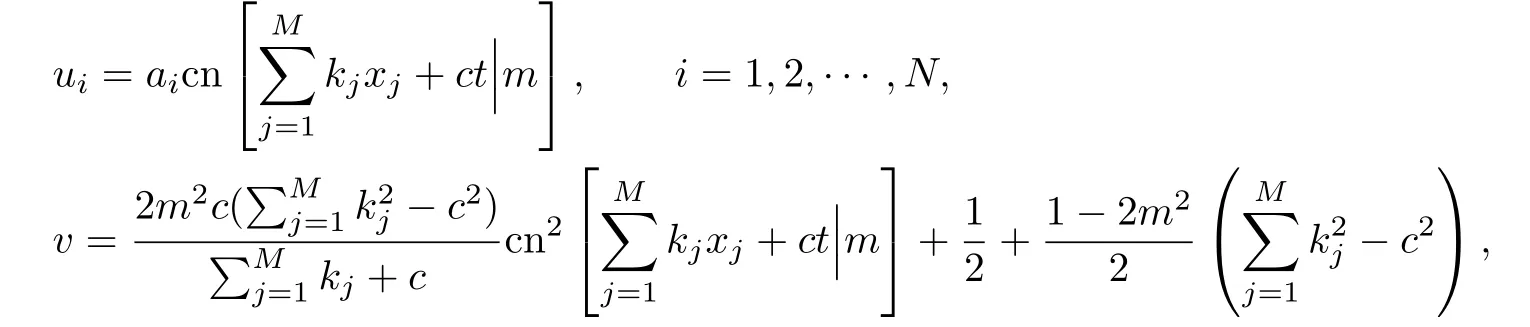
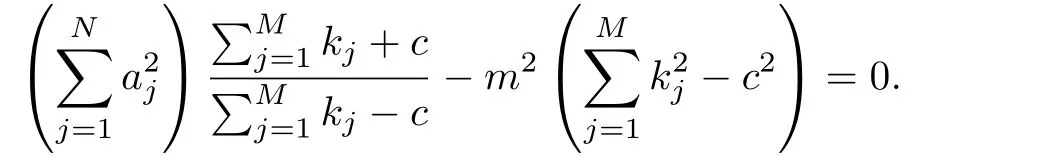
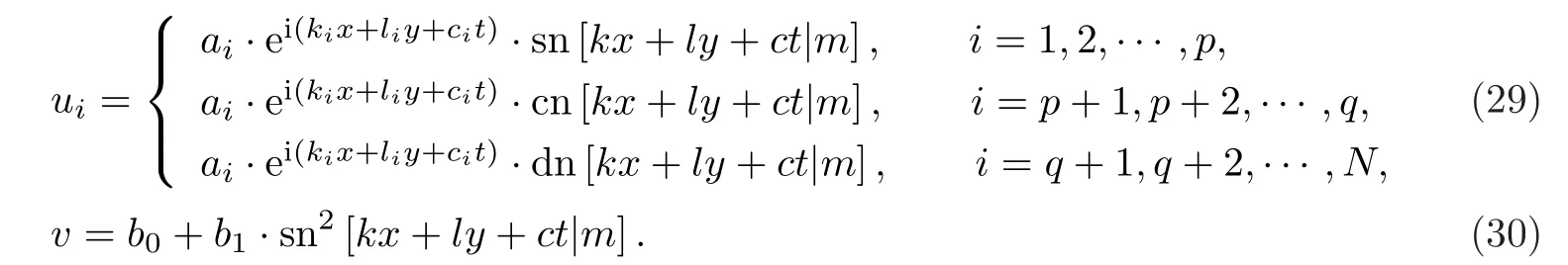
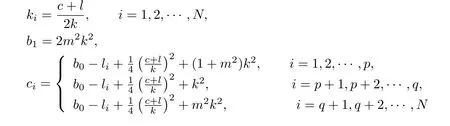

§4 结论
