一类热传导系数跳跃的非Fourier温度场分布的奇摄动双参数解
2020-07-07包立平李文彦吴立群
包立平,李文彦,吴立群
(1.杭州电子科技大学理学院,浙江杭州310018;2.杭州电子科技大学机械工程学院,浙江杭州310018)
§1 引 言
随着超短脉冲激光加热,金属快速凝固等现代高新技术的发展,热作用的周期时间短到皮秒以至飞秒量级的超急速,超常规热传导规律的研究越来越引起人们的重视.
在许多实际物理问题中,会遇到含有间断系数的扩散问题,例如,热传导过程中在不同温度下,热传导系数会出现间断[1],从而这些物理问题的数学模型就归结于间断系数问题.如何有效和准确地求解它们仍然是一个很大的挑战.虽然许多学者针对这类问题的数值求解作了大量的研究工作,但是使用经典的有限元方法求解很难获得高精度的数值解.关建飞,沈中华[1-2]等人用Fourier热传导定律描述了板状金属材料中脉冲激光激发的超声波,并用有限元方法进行了数值模拟.对于常规条件下的非稳态热传导问题,人们常常采用Fourier热传导定律来描述热流密度与温度梯度之间的关系,也足够精确,但是延伸到温度急剧变化的场合,用Fourier热传导定律来描述将存在问题,因此使用非Fourier热传导定律更合适.李金娥[3]建立了一个双层材料层合板瞬态加热情况下的非Fourier热传导分析模型,用向后差分法得到了温度场的数值解.张浙[4]对非Fourier热传导的性质,模型,模型的求解及应用与实验等几个方面的研究进展做了一个较详尽的概括与评述,并指出了今后需要着重研究的方向,采用非Fourier热传导定律来构建模型,考虑由于温度急剧变化热传导系数出现跳跃的情况,得到了非线性的具有间断系数的奇摄动双曲方程.刘法贵,葛云飞,李才中[5]考虑具间断系数线性双曲型方程组Riemann问题,利用分析的方法证明了该问题包含波解的存在性.张志娟,蔚喜军[6]讨论了一维,二维具有间断系数抛物方程的LDG方法,进行了稳定性分析,并给出了解的误差估计,但获得该结果对真解的光滑性要求比较高.张荣培,蔚喜军和崔霞应[7]用间断方法求解带有间断系数的二维椭圆方程针对扩散系数间断的特点,构造了一种新的加权对称内惩罚方法证明了相应双线性形式的连续性和强制性,并给出收敛性证明数值算例表明该方法对于求解强间断系数问题是有效的.常洛[8]考虑了间断系数抛物方程的显隐格式区域分裂有限元方法,在子区域内部应用隐式方法,子区域相邻内边界条件值由一个函数在前层的值给出,从而实现了并行计算.该方法在子区域内部和跨越内边界时都保证了问题的守恒性,经过理论分析得到了误差估计并给出了数值算例.Rauf Amirov[9]构造了新的积分来表示具有分段常导系数和间断条件的Sturm-Liouville方程的基本解,并且研究了边值问题的重要谱性质.上述文献都是通过数值模拟的方法得到相关结果.
本文考虑脉冲激光作用于材料表面基于热弹机制产生的温度场,过去通常用Fourier热传导定律描述由激光激发的温度场,但在瞬态热传导过程中(特别是某些极端情况,如激光加热等),热量传递具有和经典热传导理论所认为的扩散行为完全不同的物理机制,物理机制的差异反映在描述物理行为的数学表达式上,就是说以经典的Fourier定律为基础建立起来的热传导理论,已不能对这种情况下的热量传递规律做出合理的解释,因此采用非Fourier热传导定律构造模型,克服了这一问题.由于热松弛时间特别小,因此可以将该问题视为奇摄动双曲方程问题.通过建立模型.应用奇摄动方法来求解.康连城[10]研究了一类具有非线性初边值条件的奇摄动问题的n维拟线性双曲抛物型方程,给出了该摄动问题光滑解具有一致有效的一阶渐近展开式的存在性.文献[11]研究了一类具有变动边界的初边值问题的奇摄动的拟线性双曲抛物型方程,给出了此问题的解具有以退化问题充分光滑解为首项的广义渐近展开式的存在性.但文献[10-11]的模型并未出现系数间断的情况,宋明玲[12]研究了多维空间上具有间断系数的半线性双曲型方程柯西问题局部解的存在性和唯一性,文献[13]研究了一类具有连续势垒和不连续(左或右连续)发生器的一维反射后向双随机微分方程,得到了该随机微分方程解的存在性定理和比较定理.文献[14]介绍了一类非光滑系统的几何理论,将理论引入到综合数学中的几何学与拓扑学中.但只是研究了解的存在唯一性,并没有确定位置关系,文献[15]研究了一类漂移和扩散系数都可能不连续的一类随机微分方程的Euler-MuluyAMa逼近的强收敛性.文献[16]研究了一类非光滑的奇摄动动力系统,在系数出现间断时,利用爆破技术对非光滑动力系统进行正则化.文献[17]研究了具有间断源项的半线性微分方程奇摄动问题,针对这些问题,构造了一个适当的分段均匀网格的数值方法,该方法对于奇异摄动参数是一致收敛的,数值结果验证了理论结果.文献[1-2]提到了热传导系数出现间断的情况,但只是用有限元方法数值模拟计算的.目前来说,尚未见到关于具有间断系数的奇摄动双曲方程的研究的报导,特别是间断位置未定的情形未见研究结果.
本文用非Fourier热传导定律来描述脉冲激光作用于材料表面基于热弹机制产生的温度场,考虑由于温度急剧变化热传导系数出现跳跃的情况,得到了非线性的具有间断系数的奇摄动双曲方程.应用奇摄动双参数展开法得到该问题的展开式,并且得到了内外解的存在唯一性,进而确定了热传导系数跳跃的位置关系.并用缝接法将热传导系数发生跳跃的位置两边的解缝接起来,从而得到了解的形式渐近展开式.其次通过余项估计,得到了渐近解的一致有效性,从而得到了完整温度场的分布,为非Fourier热传导在非均匀材料领域中的应用研究提供参考依据.
§2 模型建立
现在作如下的假设:
[H1]φ(t),λ(x)是已知的任意阶连续可微函数,且φ(0)=0,φ0(t)≥0.
[H2]热传导系数
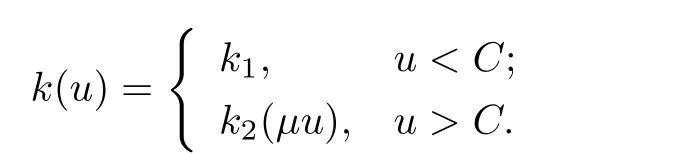
其中k1和C为正常数,k2的导函数连续,µ是小参数.假设热传导系数在u=C处发生跳跃的位置为x=ϕ(t,ε),t∗ x=ϕ(t,ε)待定. 由文献[4],可得非Fourier热传导的单相延迟热传导模型,考虑热流矢量的传播和温度梯度的关系 其中ε为相位延迟,k(u)为热传导系数.能量方程为 因此 所以 由文献[1-2]可知,在多种材料中会出现热传导系数间断的情形.因此本文讨论的(1)中的热传导系数满足假设[H1]的假定,即热传导系数跳跃的非Fourier温度场问题 初始条件和边界条件分别为 由假设[H2],k(u)是不连续的,在u=C存在一跳跃间断点,且在u=C处,x=ϕ(t,ε),t∗ 令Ω1={(x,t)∈[0,L]×[0,T]|u(x,t) 因此问题(1)-(2)可改写为 其中Ω1的边界∂Ω1={(x,t)|0≤t≤t∗,x=L}∪{(x,t)|t=0,0≤x≤L}∪{(x,t)|0≤t≤t∗,x=0}∪{(x,t)|t∗≤t≤T,x=ϕ(t,ε)},Ω2的边界∂Ω2={(x,t)|t∗≤t≤T,x=ϕ(t,ε)}∪{(x,t)|t∗≤t≤T,x=0}. 分别对(3),(4)构造形式渐近解,首先给出(3)的合成展开式 其中 将(6)代入到(3)中,比较ε的同次幂系数,可得: 比较εµ的同次幂系数,可得: 在有界域上,根据线性抛物方程理论,可得到(7)-(10)和(15)-(16)的存在唯一性. 定理1(1)中的热传导系数k(u)在u=C处发生跳跃的位置为 证令δ为充分小的正常数,kδ(u)∈C∞(R),满足 现考虑问题 边界条件和初始条件为 令 则ω1t(x,t)=−φ0(t)+(kδ(u)ω1x)x,ω1(0,t)=0,ω1(x,0)=0,ω1(L,t)=−φ(t)≤0. 应用De Giorgi迭代技术,由极值原理可得ω1≤0. 因此uδ(x,t)≤φ(t).令ω2(x,t)=uδx(x,t),可得 本文采用非Fourier热传导定律来构造温度场模型,考虑由于温度急剧变化导致热传导系数出现跳跃的情况,得到了非线性的具有间断系数的奇摄动双曲方程.应用奇摄动双参数展开法得到该问题的展开式,并且得到了内外解的存在唯一性,进而确定了热传导系数出现跳跃的位置关系.并用缝接法将热传导系数发生跳跃的位置两边的解缝接起来,从而得到了解的形式渐近展开式.其次,通过余项估计,得到了渐近解的一致有效性,从而得到了热传导系数跳跃的非Fourier温度场的完整分布.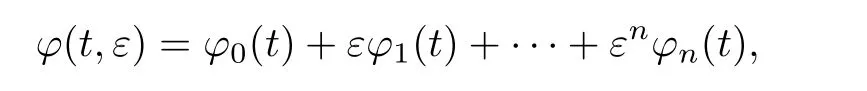





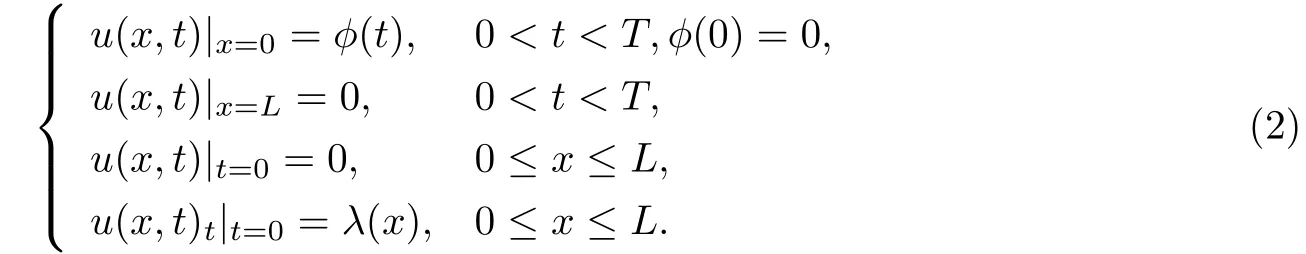

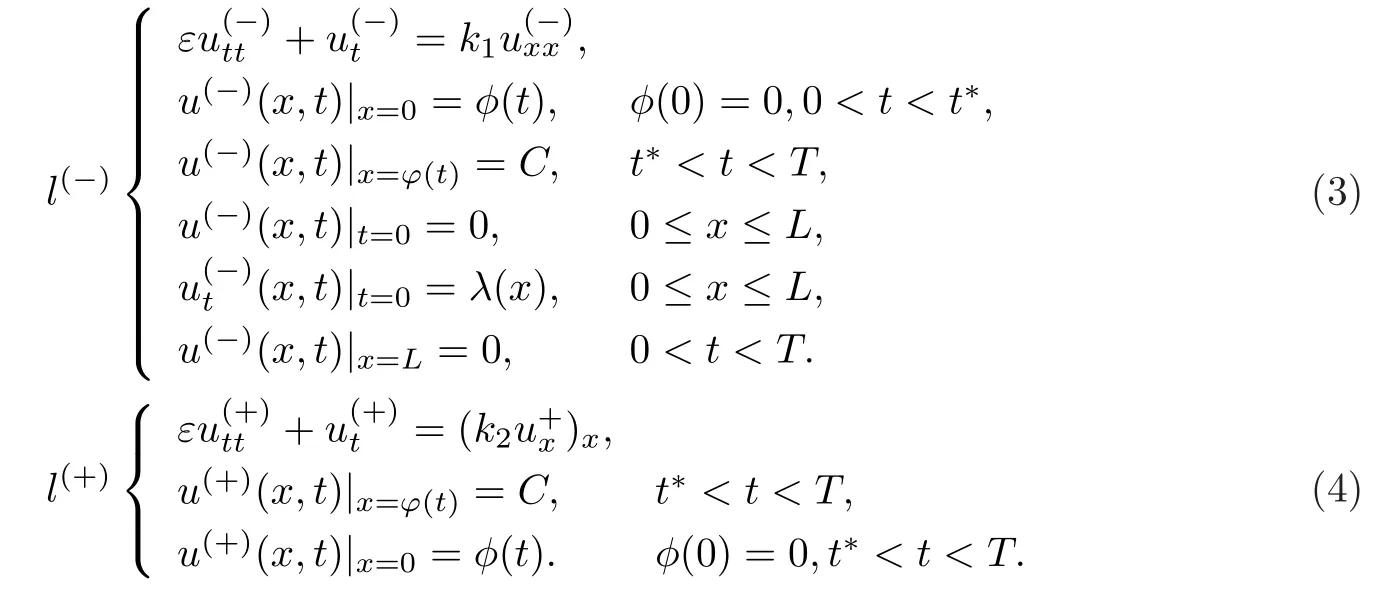
§3 形式展开
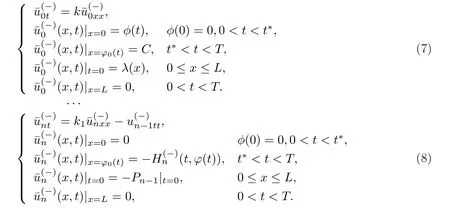


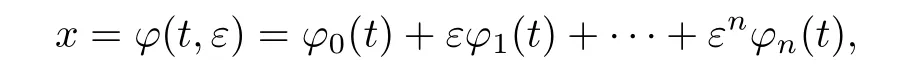
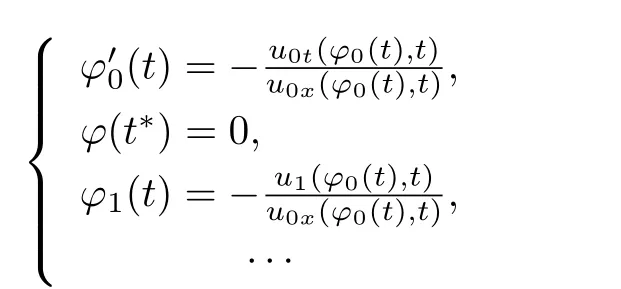
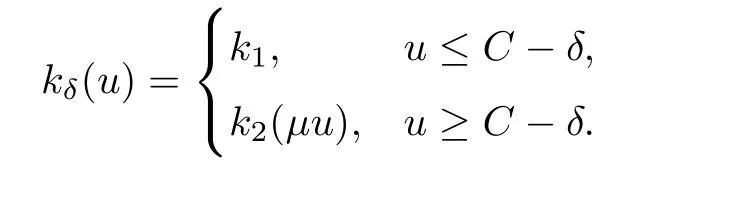

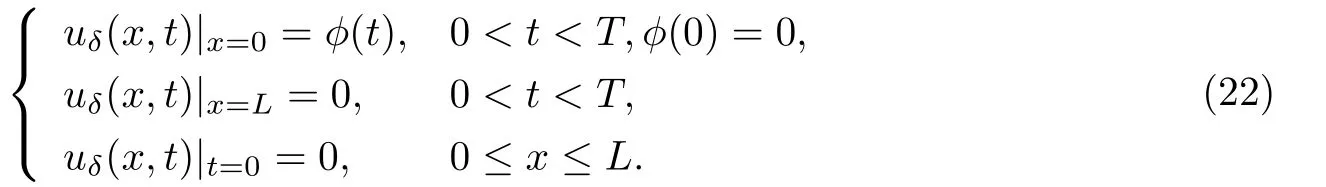
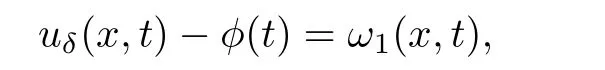


§4 余项估计



§5 结束语
