地表多层框架结构地震反应分析

张悦豪，迟世春，王茂华

(1.大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024；2.大连理工大学 建设工程学部水利工程学院 工程抗震研究所， 辽宁 大连 116024)

近年来，随着城市的快速发展，人们对于地下空间的使用日趋增多。一般认为，地下结构受到周围岩土体的约束，其抗震安全性能高于地上结构，导致对地下结构的抗震研究有所忽视。但1995年发生的阪神大地震[1-3]中，许多地下结构受到了严重的破坏，如大开地铁站站内的中柱几乎全部破坏，顶板破坏引起地面塌陷严重，以及2008年发生的汶川地震，大量的隧道结构发生了不同程度的破坏。一系列地下结构的安全性问题引起了全世界专家和学者们的重视。

很多地面建筑都含有下部结构，如地下停车场，地下大型商场等。目前对于地表结构及地下结构的抗震研究已有一定进展[4-8]，地上和地下结构地震反应特性有很大区别，其抗震设计方法也有所不同。对于地上结构，主要的抗震设计方法包括底部剪力法、振型分解反应谱法以及时程分析法。对于下部结构，早期延用了地面建筑的抗震设计方法，即采用地震系数法[9]进行设计。在20世纪60年代，Newmark等提出了自由场变形法[10]，该方法认为由于地震引起的地下结构的变形，与该位置处自由场反应的变形一致。Penzien等人建立了柔度系数法[11]，该方法认为土体和结构的抗侧刚度不同会引起的体系之间的相互作用，在方法中加入了这部分考虑。后来日本学者提出反应位移法[12]和反应加速度法[13]，已广泛应用于地下结构的抗震设计，刘晶波等基于地上结构的Pushover分析方法和反应加速度法提出地下结构Pushover分析方法[14-16]。从以上的简化方法中可以看出，地下结构由于受到周围土体的包裹，其地震反应主要取决于围岩土体的变形，这与上部结构的动力响应主要取决于结构的动力特性有所不同[17]。

本文基于黏弹性人工边界考虑相互作用的影响[18-19]，以某含有三层地下室的框架结构为背景建立有限元模型，通过ANSYS进行结构整体有限元分析。并得到了一些规律，给工程人员提供一定的参考。

1 有限元模型

1.1 模型概况

模型为现浇框架结构，地上6层，地下3层，地下室层高4 m，其余层高3 m，柱尺寸600 mm×600 mm，梁尺寸250 mm×400 mm，混凝土强度为C30。地下室顶板厚度为300 mm，底板厚度为500 mm，外墙厚度为400 mm。地基土长度30 m，宽度30 m，深度60 m，结构与土体均采用线弹性模型。结构梁、柱采用不同截面特性的梁单元Beam 188；地下室墙体采用壳单元Shell 163；地基土体采用体单元Solid 45，其有限元模型如图1所示。场地土划分为4层，土层相关参数见表1。土体动力参数[20]见图2。

图1 有限元模型

图2 土体动力本构曲线

表1 场地土参数

1.2 阻尼和接触

瑞雷阻尼可以较好的反应土层的阻尼性质，因此在ANSYS中采用，阻尼矩阵表达式如下：

C=αM+βK

(1)

其中，α，β分别为瑞雷阻尼的质量阻尼系数和刚度阻尼系数，通过下式来确定。

(2)

(3)

其中，ω=2πf，f为结构自振频率，采用前两阶频率。

真实情况下，土体和地下室外墙这两种材料刚度差距是很大的，可以通过在ANSYS中设置接触面来模拟它们之间的动力接触关系。结构的刚度较大，用Targe 170单元来模拟，地基土体的刚度较小，用Contact 173单元来模拟。

1.3 边界条件

结构-地基的动力相互作用是一个开放系统问题，由于结构体系复杂，往往采用有限元的数值方法进行分析，在这个过程中需对无限域进行模拟，可采用人工边界完成。

在多种人工边界中，黏弹性人工边界模拟效果好，且易在ANSYS中实现，被广泛应用。本文采用集中黏弹性人工边界，弹簧和阻尼参数见文献[21-23]。由于边界节点多，且每个节点的参数都不一样，需要编写程序输入，人工边界的弹簧阻尼系数如下：

(4)

C=ρc∑Ai

(5)

其中:ρ为土体的密度；α为弹簧单元的系数；G为土体的剪切模量；R表示结构振动引起的散射波源到边界节点的距离；c为波速，对于边界节点阻尼器为法向的取压缩波波速cp，对于边界节点阻尼器为法切向的取剪切波波速cs；∑Ai为人工边界节点所代表的影响面积。

2 荷载和工况

2.1 地震波的选择

2.2 地震动等效输入

地震动输入采用等效节点力法，文献[24-27]将自由场地震动的位移、速度和应力转换为等效节点荷载作用在人工边界上。

(6)

2.3 Fourier谱强度频率匹配度

地震动的傅里叶幅值谱可反应一定频谱特性[28]，文献[29]根据地震动的Fourier幅值谱的频率和结构自振频率的相近关系，以及与该频率对应的Fourier幅值的大小程度，基于共振的原理提出Fourier谱强度频率匹配度的概念，并将其分为以下三种。

图3 Kobe波时程和傅里叶谱

(1) Fourier谱强度卓越频率匹配度为：

(7)

其中：fp表示傅里叶谱中的卓越频率；cp为fp对应的幅值；cmin为c1，c2，c3中的最小值；c1，c2，c3分别为三个最大的傅里叶幅值；fn为结构第n阶振型频率；c=max(|fp-fj| )。

(2) Fourier谱强度三大峰值频率匹配度为：

(8)

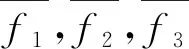
(3) Fourier谱强度平均频率匹配度：

(9)

(10)

式中：f*为地震动平均频率；c*为f*对应的傅里叶幅值；cmax为c1，c2，c3中的最大值；e=max(|f*-fn| )。

2.4 工况选择

地下结构和地上结构地震反应特性有很大区别，已有研究表明[30]，地上结构的地震反应主要受结构惯性效应影响，地下结构地震反应过程中，结构的惯性效应对结构地震反应的影响有限。由于地下结构受到周围土体的包裹，因此场地土的特性对其地震反应影响较大，地震动强度参数对于上下部结构地震反应的影响也很重要[30]。

为了体现上下部结构的动力反应特性，本文分别研究了地震动峰值加速度，地震动频谱特性，上部结构频率和土体惯性效应对结构的地震反应的影响。由以往震害表明，结构柱、结构地下部分顶底板和侧墙是薄弱环节，选取这几个截面作为控制截面进行弯矩、剪力、轴力分析。

3 结构与场地动力特性的影响

3.1 动力特性

结构的动力特性通过结构振型对应的自振频率来反应，本文分别计算了地表框架结构、单独的场地和土-结构体系的自振频率。计算结构自振频率时，将结构底边界固定。计算土-结构体系的自振频率时，将场地和体系的底边界固定，侧面边界采用法向约束，计算结果见表2。

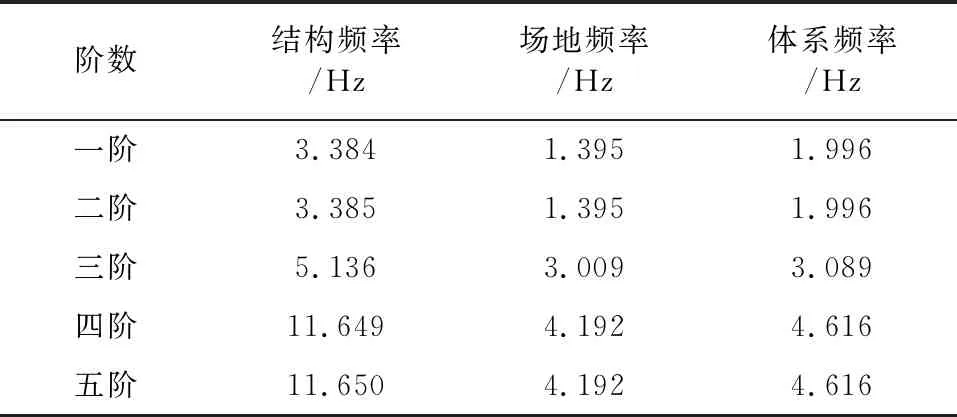
表2 自振频率

3.2 不同场地动力特性地震响应

工况选择：本文通过改变土体密度来改变土体动力特性，分别取实际情况土体密度的2.0倍、1.5倍、1.0倍、0.5倍和0.1倍建立土-结构相互作用模型，模型参数对应工况对照表3，其中，工况3对应土体密度实际情况，工况5为0.1倍实际土体密度，视为忽略土体惯性效应。

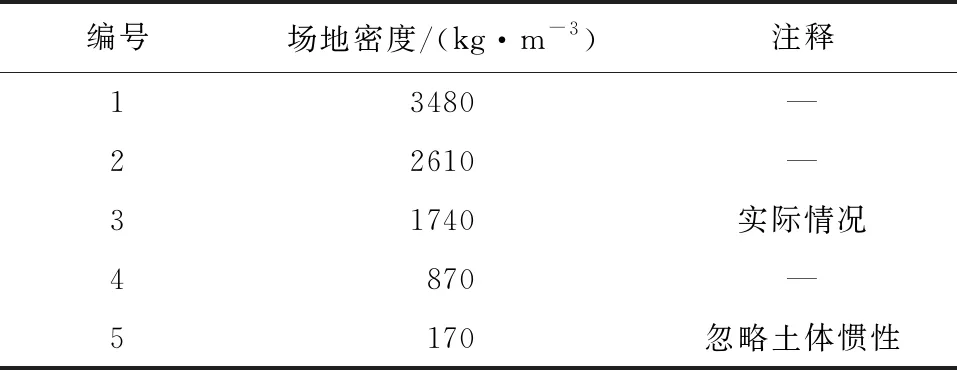
表3 工况表

地震反应的控制截面选取：截面1(底板处中柱)和截面2(顶板处中柱)进行分析。统一在模型底部输入经过调幅的Kobe地震波，幅值0.035g，持时20 s，时间间隔0.01 s。

表4为不同土体密度对应截面内力幅值，对于截面1，忽略土体惯性效应对剪力影响达到43%，对弯矩影响达到40%。对于截面2，忽略土体惯性效应对剪力影响达16%，对弯矩影响达17%。可见土体惯性特性对地下结构影响较大。图4、图5为截面1和截面2在工况3和工况5情况下的剪力和弯矩时程图。

表4 不同工况截面剪力弯矩峰值

图6为各工况下弯矩剪力极值沿高程的分布，可以看出土体自振特性对结构地下部分的地震反应有较大影响，服从一定规律，土体密度越大，结构地下及地上部分的地震反应越大。

3.3 不同结构动力特性地震响应

上部结构的动力特性可通过其自振频率来反应，本文通过改变上部结构弹性模量，密度来改变上部结构的频率。在模型底部输入经过调幅的Kobe地震波，幅值0.035g。分析结构地震反应，对于结构地下室中柱，结构频率的改变对其受力影响较小，但对于结构地上部分中柱的受力影响较大。随着结构频率的增大，结构地上部分中柱的剪力、弯矩、轴力表现出明显的规律性。即随着上部结构频率的增大逐渐减小。

图4 截面1内力时程图

图5 截面2内力时程图

4 地震动特性的影响

4.1 不同地震动频谱特性地震响应

本文选取已有记录的多条天然地震波，并对其统一调幅至建筑抗震规范中7度多遇地震对应的地震加速度。从模型底部的基岩位置处输入地震动时程，研究频地震动的频谱对结构体系的影响。

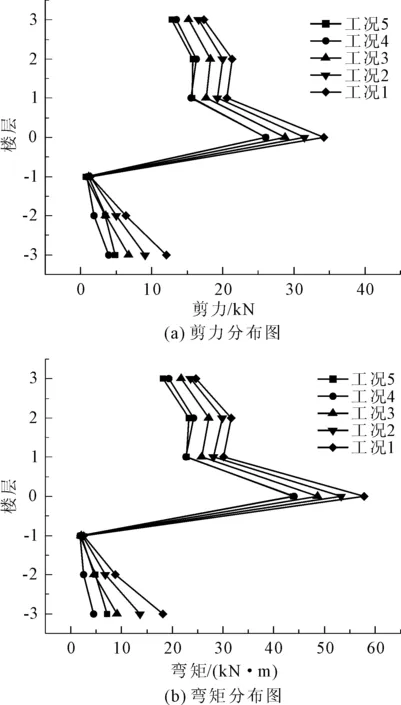
图6 不同土体密度中柱地震反应

表5为结构基频对应的三种Fourier谱强度频率匹配度，由计算结果可知，四种地震波的Fourier谱强度卓越频率匹配度从大到小依次是Imper波、Friu波、Loma波、Kobe波；Fourier谱强度三大峰值频率匹配度从大到小依次是Loma波、Friu波、Kobe波、Imper波；Fourier谱强度平均频率匹配度从大到小依次是Loma波、Kobe波、Imper波、Friu波。

表5 不同地震动对应的Fourier谱强度频率匹配度

分析表6可知，结构地下室顶底板，地下室侧墙和结构地上部分中柱的剪力弯矩反应由大到小依次是Loma波、Kobe波、Imper波、Friu波，这个结果与Fourier谱强度平均频率匹配度的大小顺序一致，使用Fourier谱强度平均频率匹配度能较好的反映地震作用下频谱特性对结构地震反应的影响。但是对于结构地下室中柱，不同频谱的地震动对其地震反应影响较小，无明显规律。

表6 不同地震动频谱对应结构地震响应

4.2 不同地震动幅值地震响应

依据《建筑抗震设计规范》[31](GB 50011—2016)中表5.1.2-2中的规定，本文分别计算了6度、7度、8度、9度多遇地震影响下的结构的地震反应。地震波选取经过调幅的Kobe地震波，峰值分别为0.018g、0.035g、0.07g和0.14g，从模型底部输入。

分析结构中柱的地震反应，中柱的地震反应大小整体上随着地震动幅值的增大而增大。地表以下部分的中柱，受力大小虽然不尽相同，但是整体分布一致，弯矩和剪力在底板和顶板位置处相对较大，中部较小，整体呈现出剪切变形的模式。由于考虑自重的影响，轴力相对较大，6度、7度地震作用下轴力由下至上逐渐减小。8度、9度强度较高的地震作用下，在地表处轴力有放大。

5 结 论

文章考虑土体-结构动力相互作用，建立整体分析模型，对其进行地震作用下的动力反应分析。主要结论如下：

(1) 地震作用下，不同工况下的地下室中柱受力大小虽然不尽相同，但具有一定规律性。弯矩、剪力在底层位置处较大，向上逐渐减小，地表面处达到峰值，整体呈现剪切变形的模式。轴力由下到上呈现递减趋势，峰值出现在地下室底层位置处。由于土体对地下室的约束作用，结构地下部分的地震反应相对于结构地上部分的地震反应较小。

(2) 地震动频谱特性对地下室中柱的地震反应影响较小。对于地下室顶底板及侧墙和结构地上部分的中柱，Fourier谱强度平均频率匹配度可较好的反映结构和地震动因共振效应引起的结构地震反应的放大，Fourier谱强度平均频率匹配度越大，结构地震反应越明显。地震动幅值对结构地震反应影响较大，并且随地震动幅值增大，结构地上部分和地下部分地震反应均明显增大。

(3) 以地基土体的密度反应土体的动力特性，可知忽略土体的动力特性对地下室中柱的地震反应的影响可达到43%，而忽略结构的动力特性对地下室中柱的地震反应影响相对较小，不到10%。通过改变结构的材料参数改变结构的自振频率，可知在相同的地震动作用下，结构的自振频率对地下室的地震反应影响较小，但对于地面以上结构，结构自振频率的改变对其影响较大。