后掺骨料混凝土框架边节点恢复力模型研究

贾金青，毛鹏飞，张丽华，张 强，郑婉婷

(大连理工大学 海岸与近海工程国家重点实验室， 辽宁 大连 116024)

在当今社会，泵送商品混凝土技术是一种被广泛采用的施工技术。与普通混凝土相比，泵送混凝土为满足其可泵性，通常采取减小粗骨料粒径(粗骨料粒径不宜超过泵管内径的1/4)[1]和增大水泥用量等措施。研究表明，水泥用量大和粗骨料粒径减小会导致混凝土中水泥浆体富裕过大，不利于骨料发挥强度骨架和嵌锁作用[2-3]，进而出现混凝土早期开裂严重的问题[4]。

后掺骨料混凝土是指在基准混凝土(泵送混凝土)的基础上，后掺一定体积分数的粗骨料，二次搅拌均匀后再进行浇筑和振捣。与基准混凝土相比，单位体积混凝土中，粗骨料含量提高，水泥含量降低，可以有效改善早期开裂现象，并且可以降低成本，具有经济和环保价值。将泵送混凝土技术和后掺骨料工艺相结合，贾金青[5]提出一种绿色混凝土施工设备及施工方法，可以实现在待浇筑楼层后掺一定体积分数的粗骨料并进行二次搅拌均匀。

沈卫国[6]通过均匀抛入不同体积率的粗集料，研究表明混凝土的强度和弹性模量在体积置换率为20%时达到最大，随后有所降低。胡玉龙[7]通过对后掺骨料泵送混凝土梁抗剪性能进行试验，研究表明在15%抛填率下，泵送混凝土抗压强度及梁的抗剪承载力均有较大提高，且工作性能满足要求。贾金青等[8]通过6根不同后掺率的简支梁进行抗弯试验，研究表明C40泵送混凝土的最佳粗骨料后掺率为20%。贾金青等[9]通过5根后掺骨料钢筋混凝土柱进行大偏心受压试验，研究表明在20%骨料后掺率下，柱的极限承载力最大。贾金青等[10]通过5根后掺骨料钢筋混凝土柱进行小偏心受压试验，研究表明后掺率为10%的混凝土柱试件延性最好，后掺率为20%的混凝土柱试件的延性与普通混凝土柱相近。

目前对后掺骨料混凝土抗震性能的研究还很少，已有研究表明，后掺率为20%混凝土的抗压强度、抗冻以及抗氯离子渗透等性能较好[11-12]。因此，本文基于7个后掺率为20%的边节点试件的拟静力试验结果，考察试验轴压比和核心区体积配箍率对其抗震性能的影响，并在试验的基础上，采用三折线模型和回归分析方法，建立恢复力模型，以期为后掺骨料混凝土框架节点弹塑性地震反应分析提供参考。

1 试验概况

1.1 试验材料

试验采用P.O42.5R级普通硅酸盐水泥，Ⅰ级粉煤灰，细骨料为天然河砂(中砂)，基准粗骨料为5 mm～16 mm连续级配石灰石碎石，后掺粗骨料为10 mm～20 mm连续级配石灰石碎石，拌合用水采用自来水，并添加ViscaCrete3301聚羧酸高效减水剂。根据“强柱弱梁”的抗震设计理论，柱采用后掺率为20%的C40混凝土，梁采用后掺率为20%的C30混凝土。混凝土配合比依据规程进行计算以及试拌而得[13]，柱配合比为(水泥+粉煤灰)∶石子∶砂子∶减水剂∶水∶后掺粗骨料=1∶1.781∶1.456∶0.011∶0.403∶1.310，梁配合比为(水泥+粉煤灰)∶石子∶砂子∶减水剂∶水∶后掺粗骨料=1∶2.324∶2.061∶0.013∶0.489∶1.590。

1.2 试件编号及主要参数

试验设计了7个边节点试件，后掺率均为20%，试件主要参数见表1。梁、柱尺寸及配筋见图1。

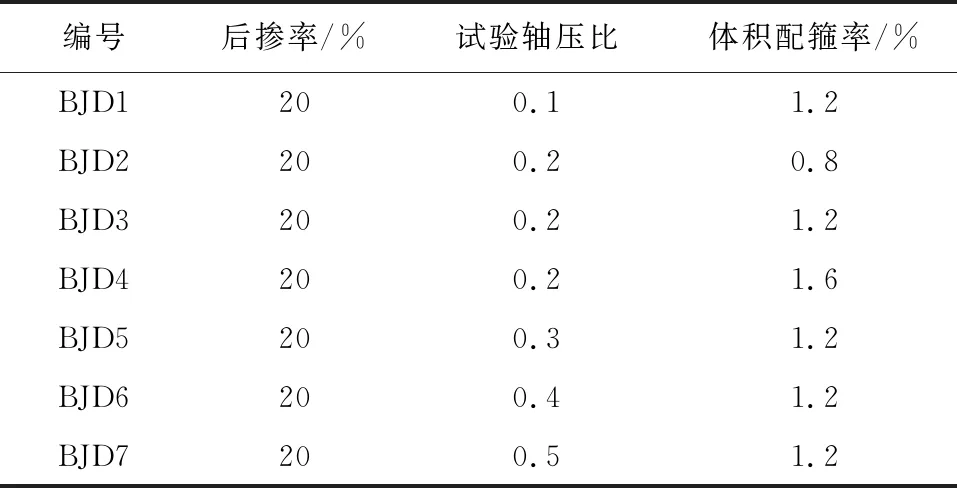
表1 试件主要参数

图1 试件尺寸及配筋(单位：mm)

1.3 基本力学性能指标

依据《金属材料拉伸试验》[14](GB/T 228.1—2010)和《混凝土物理力学性能试验方法标准》[15](GB/T 50081—2019)的标准实验方法，测得钢筋及混凝土伴随试块的基本力学性能如表2、表3所示。

表2 钢筋基本力学性能

表3 混凝土基本力学性能

1.4 加载装置及加载制度

本试验采用梁端加载方式，在柱端施加恒定轴压力，在梁端施加低周往复荷载，加载装置实图见图2，示意图见图3。采用力-位移混合加载制度[16]，在试件屈服之前，采用荷载控制，每级荷载增量约为预估屈服荷载的25%，循环一次，试件屈服之后，采用位移控制，每级位移增量约为10 mm，循环三次，直到试件的承载力下降到峰值荷载的85%[16]，结束试验。加载制度见图4。

图2 加载装置实图

图3 加载装置示意图

图4 加载制度

2 恢复力模型的建立

2.1 骨架曲线特征点的确定

考虑本试验试件的加载受力过程，采用三折线恢复力模型，将骨架曲线简化为三段，分别为弹性段、屈服-峰值段和峰值-破坏段。骨架曲线计算模型包含六个特征点：正(反)向屈服点、正(反)向峰值点、正(反)向破坏点。由于各个试件的滞回曲线存在一定的差异，难以用统一的方式表达出来，因此需要对各试件的骨架曲线进行无量纲化[17]。本文以各试件的峰值点(Δmax，Pmax)为基准点进行无量纲化，横坐标表示为Δ/Δmax形式，纵坐标表示为P/Pmax形式[18]，将各试件无量纲化后的骨架散点汇总于图5，可以发现较好的规律性。

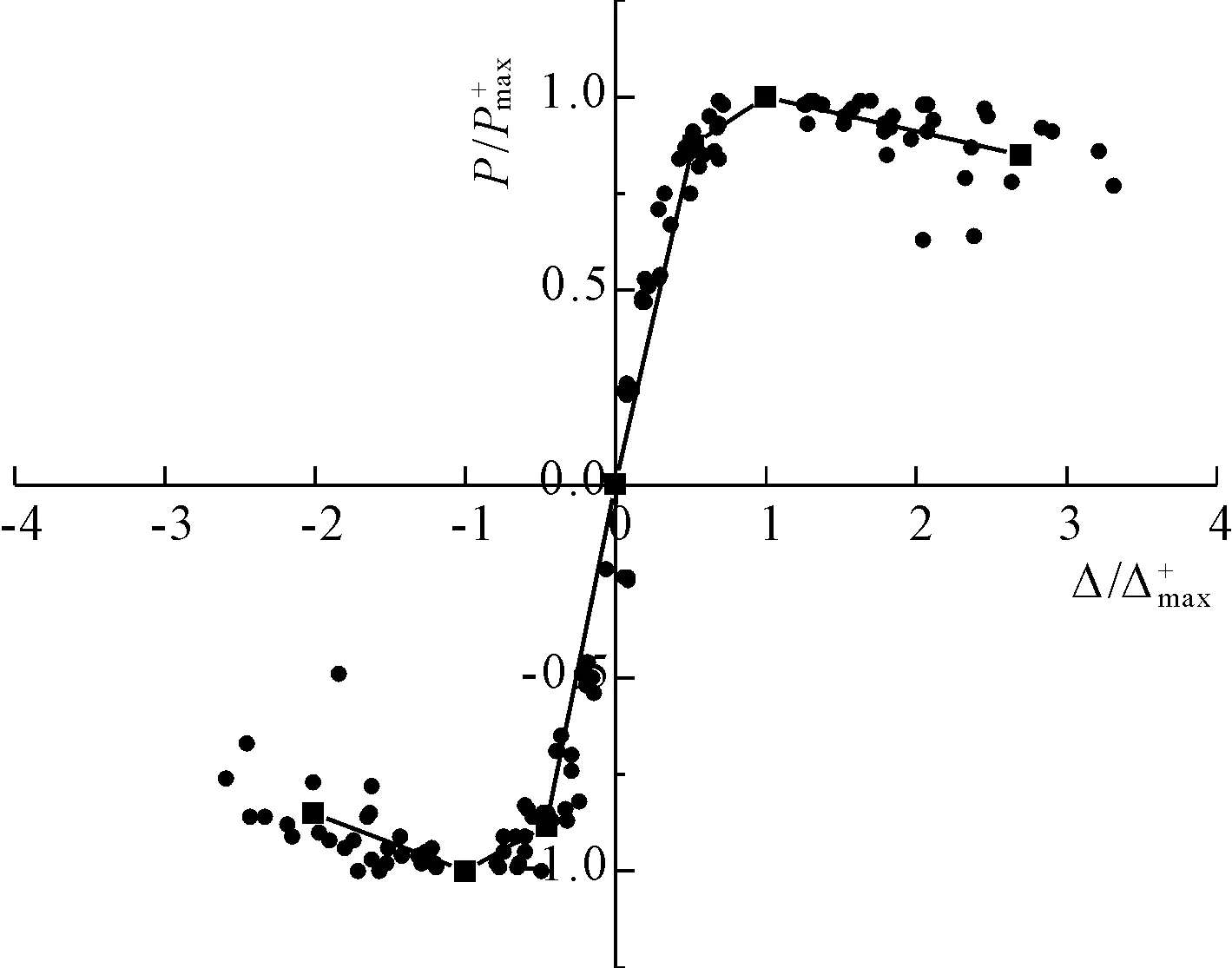
图5 各试件无量纲化骨架散点

采用Excel的趋势线功能对各段的散点进行线性拟合，得出各段的数学表达式如表4所示。取破坏点荷载Pu=0.85Pmax，进而可以确定各特征点的坐标，得出骨架曲线计算模型，如图6所示。

表4 三折线各段的线性回归方程

图6 骨架曲线计算模型

2.2 刚度退化规律

如图7所示，以K1(K3)表示正(反)向卸载刚度，K2(K4)表示反(正)向加载刚度。随着低周往复加载的进行，试件的加载刚度和卸载刚度会出现退化现象。具体表现为：1→2、5→6均为正向卸载线，而5→6的斜率比1→2的小，表明正向卸载刚度出现退化；2→3、6→7均为反向加载线，而6→7的斜率比2→3的小，表明反向加载刚度出现退化。为描述刚度退化规律，通过回归分析，建立加卸载刚度随加卸载点位移的计算公式。

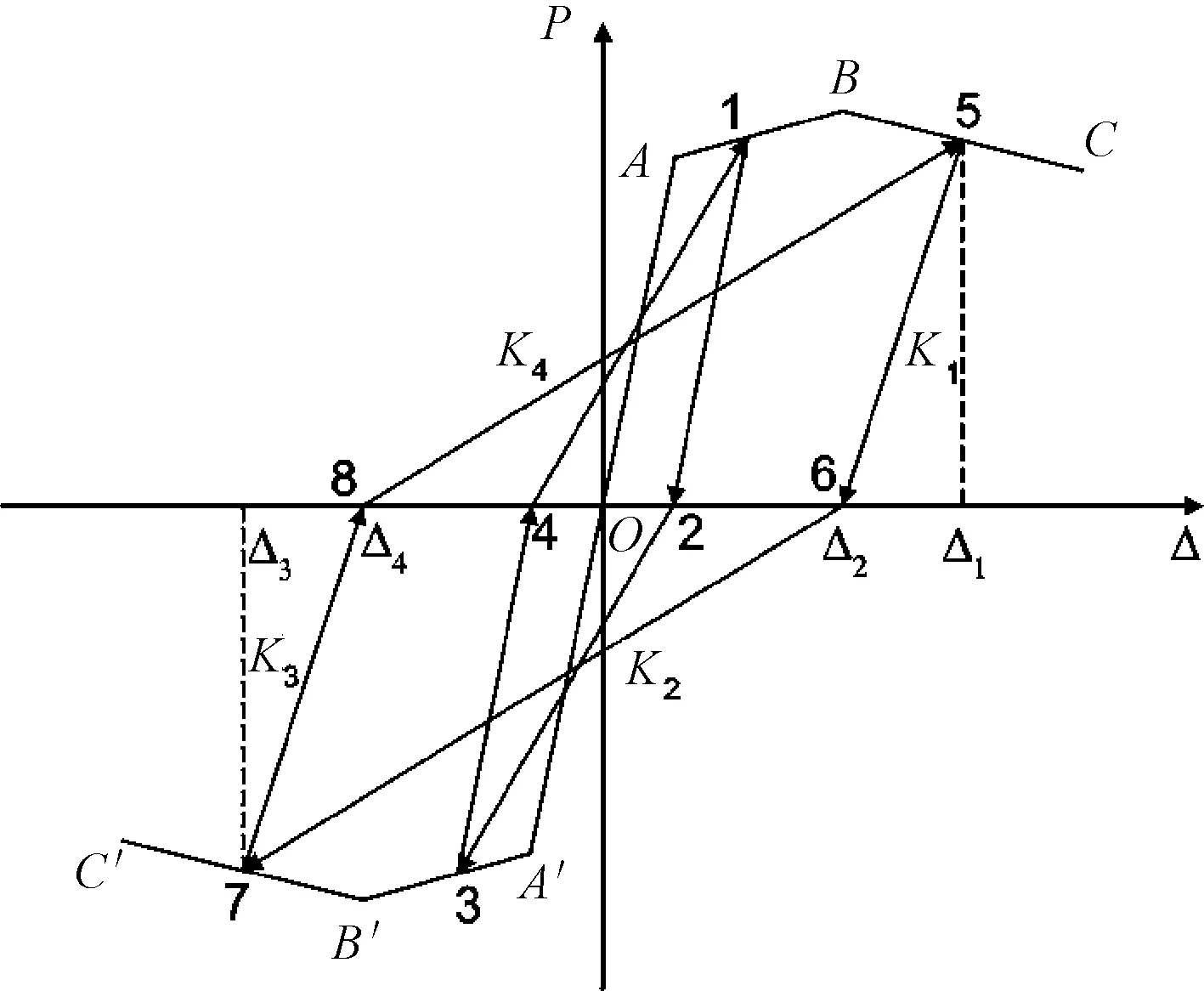
图7 刚度退化

(1)

图8 K1退化曲线

(2)

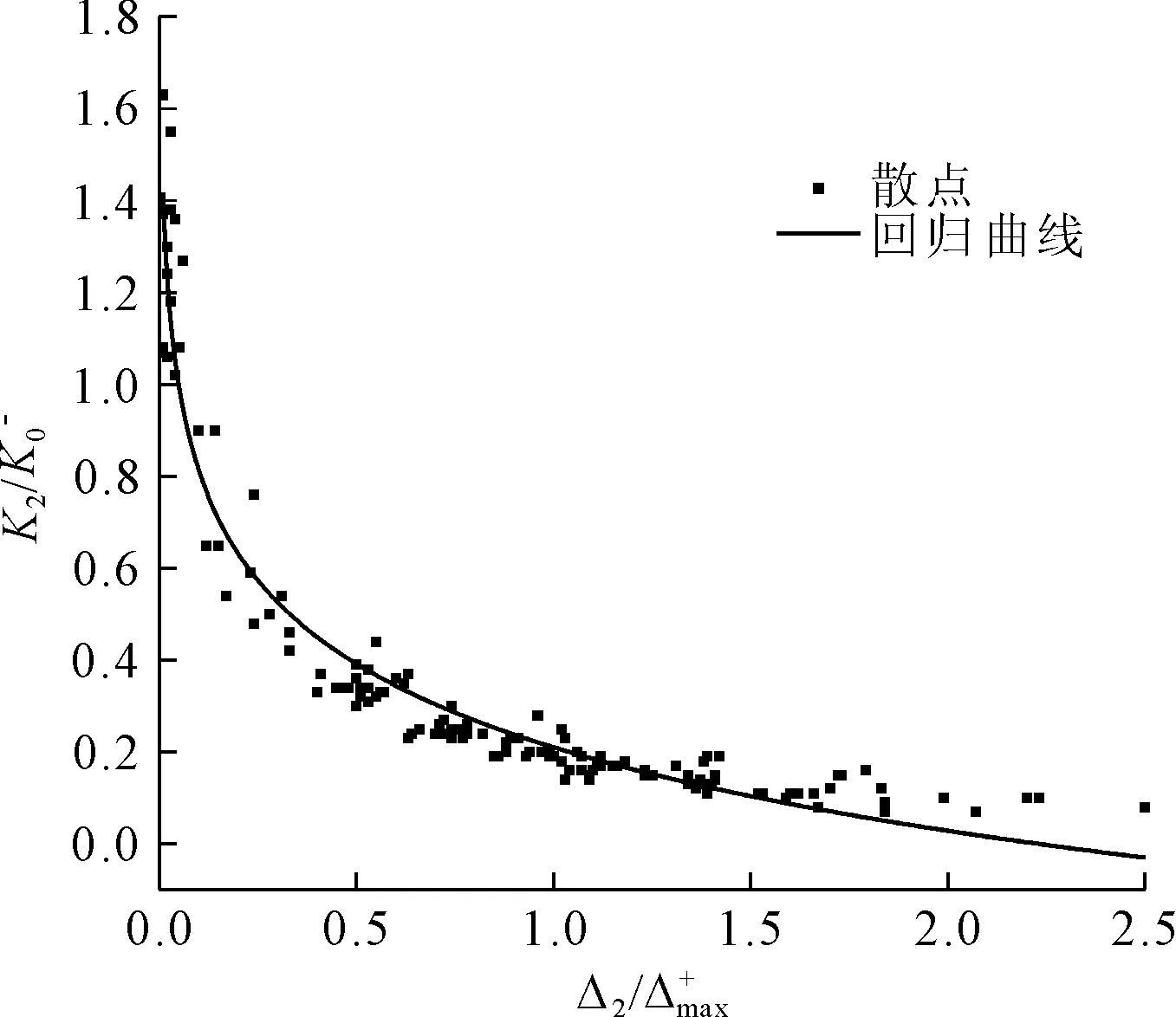
图9 K2退化曲线

(3)

图10 K3退化曲线

(4)

2.3 滞回规则

滞回规则如图7所示，说明如下：

(1) 当试件处于弹性阶段时，正(反)向加载沿OA(OA′)，正(反)向卸载沿AO(A′O)，正向加(卸)载刚度为正向初始刚度，反向加(卸)载刚度为反向初始刚度。

图11 K4退化曲线

(2) 当试件处于屈服-峰值阶段时，正向卸载沿1→2进行；反向加载以正向卸载残余位移点2为起点，若试件反向未屈服，加载路径为2→A′→B′→C′，反之，加载路径为2→3→B′→C′；反向卸载沿3→4进行；正向加载路径按4→1→B→C进行。

(3) 当试件处于峰值-破坏阶段时，正向卸载沿5→6进行；反向加载以正向卸载残余位移点6为起点，若试件反向未达到峰值荷载，加载路径为6→B′→C′，反之，加载路径为6→7→C′；反向卸载沿7→8进行；正向加载路径沿8→5→C进行。

3 恢复力模型验证

根据骨架曲线计算模型中各特征点的坐标，可以得出各试件的计算骨架曲线，计算骨架曲线与试验骨架曲线的对比如图12所示。根据骨架曲线计算模型和滞回规则，可以得出各试件的计算滞回曲线，计算滞回曲线与试验滞回曲线的对比如图13所示。

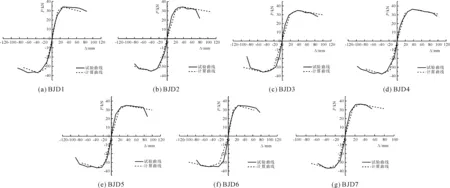
图12 计算骨架曲线与试验骨架曲线对比

图13 计算滞回曲线与试验滞回曲线对比

由图12和图13可知，虽然计算曲线与试验曲线在局部存在一定的差异，这主要是部分数据离散性略大、恢复力模型本身与实际工程存在一定误差综合导致的，但是，从总体而言，计算曲线与试验曲线吻合良好，本文所建立的三折线恢复力模型可以反映后掺骨料混凝土框架边节点在低周往复荷载作用下荷载-位移的关系，可为后掺骨料混凝土框架边节点的抗震性能和弹塑性动力反应分析提供参考。

4 结 论

(1) 在低周往复荷载作用下，各试件主要经历弹性、屈服强化以及破坏三个阶段。随着加载的进行，加载刚度、卸载刚度出现退化现象。试件屈服之后，卸载出现残余变形，且残余变形随加载级次的增大而增大。

(2) 各试件的滞回曲线呈梭形且饱满程度较好，表明试件具有良好的耗能能力和滞回性能。

(3) 计算曲线与试验曲线吻合良好，本文所建立的三折线模型，可以反映后掺率为20%的框架边节点在低周往复荷载作用下的荷载-位移关系，可为后掺骨料混凝土框架节点弹塑性地震反应分析提供参考。