玻尔氢原子模型中德布罗意波的最概然解释

雷 勇

(南京信息工程大学物理与光电工程学院大学物理部，江苏 南京 210044)

1 提出问题

玻尔氢原子模型在量子理论发展史上有着非常重要的地位，在模型中玻尔根据对应原理思想得出了氢原子轨道稳定性的量子化条件：只有电子角动量为(即约化普朗克常量)整数倍的那些轨道才是稳定的[1, 2]。根据对应原理确定某个体系的量子化能级需要知道系统轨道运动的频率对能量的依赖关系，这通常比较麻烦，但是如果反过来，把角动量量子化条件作为出发点，往往可以比较容易求出体系的量子化能级。此外，量子化条件与经典力学并不相容，带有一定的人为假设性质，并未从根本上解决不连续的本质[3]，因此当时的物理学家希望能对量子化条件给予更深刻的物理解释。英国物理学家布里渊曾设想原子核周围存在以太波，这种波是由电子运动激发的。该波相互干涉，只有在特定合适的轨道半径时才能形成绕原子核的驻波，因为轨道半径是量子化的[4]。

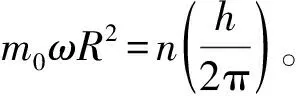
λn=2nπa0

(1)

其中a0是玻尔半径。

尽管德布罗意利用相位波理论解释了量子化条件，但是从后来建立的量子力学角度看，其解释有明显的局限性。薛定谔于1926年发表在《物理学年鉴》的第一篇论文[6]中从经典的雅可比-哈密顿方程出发，并引入作用量函数S=Klogψ(K是一常量)，利用变分法得到描述氢原子的方程：

(2)

式中，E为电子能量；e为电子电量绝对值；r为电子相对原子核的距离。在考虑函数ψ的单值性和有限性后，当E为负值时，方程(2)中E的解为

(3)

得到和玻尔氢原子模型一样的能级。薛定谔进一步写到：“我……最终……以上述更为中性的数学形式给出了它们，因为它揭示出了真正本质的东西。在我看来，真正本质性的东西，在于‘整数’假设无须再神秘地引入量子化规则，而是通过进一步回溯问题，从而发现‘整数性’根植于某个空间函数的有限性和单值性。”[6]薛定谔的解释显然不同于德布罗意。不仅如此，氢原子本征态波函数ψnlm也不是动量的本征函数，所以ψnlm的德布罗意波长没有确定的值，而呈现一定的分布，这显然与德布罗意的解释不同。此外，玻尔模型中氢原子能级不存在简并问题，而量子力学解存在简并问题，如下文所述不同的简并态对应的德布罗意波长分布并不一样。

尽管德布罗意的解释有明显的局限性，但是我们不应该简单地认为德布罗意的解释是错误的或者纯属巧合，应该进一步探究其内在原因。量子力学的计算结果显示玻尔氢原子模型中的半径其实是由|Rn(n-1)r2|2得到的最概然半径[3]，其中Rnl为径向函数，可以看出最概然半径仅仅取决于氢原子波函数ψnlm=Rnl(r)Ylm(θ,φ)中的径向函数Rnl(r)部分。我们可以据此推测，玻尔氢原子模型的德布罗意波长λn=2πna0是否具有类似的最概然解释呢？本文基于上述推测，研究了氢原子不同量子态下的径向函数对应的德布罗意波长概率分布，发现λn有类似的最概然解释。

2 计算、分析和讨论

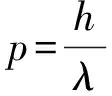
径向函数Rnl(r)由坐标表象到动量表象的变换关系为[7]

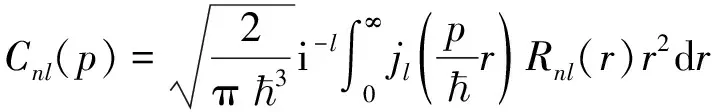
(4)

其中jl是球贝塞尔函数。参考文献资料的一般做法，下面只列出n=1、2、3的计算结果，相应径向函数有6个：R10、R20、R21、R30R31、R32。计算结果显示上述径向函数对应的德布罗意波长概率分布的极值个数并不相同，据此可将这6个态分为两类：第一类是R20、R30、R31，在λ∈(0,∞)范围内，德布罗意波长概率分布有多个极大值，这类情况与我们要讨论的问题无关，所以不再列出它们的具体计算结果；第二类是R10、R21、R32，在λ∈(0,∞)范围内，德布罗意波长概率分布只有一个极大值，这类情况与我们要讨论的问题密切相关。为什么它们只有一个极大值呢？这源于氢原子径向函数的自身特点。氢原子的径向函数可以写为[3]

(5)

其中u(r)满足方程

(6)

函数u(r)，进而径向函数Rnl(r)的行为由径向量子数nr决定[3]。由于nr=n-l-1，所以第二类径向函数有nr=0，此时的径向函数可表示为

(7)

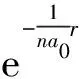
径向函数R10、R21、R32表示如下：

(8)

相应的球贝塞尔函数表示如下：

(9)

根据公式(4)，径向函数R10在动量空间的表示，即动量概率振幅为

(10)

动量的大小在p～p+dp范围内的概率为

(11)

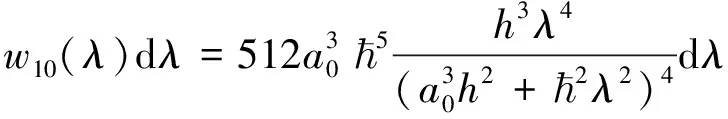
(12)

在λ∈(0，∞)范围内，当λ=2πa0时w10(λ)有最大值，即R10的最概然德布罗意波长λp1=2πa0，等于公式(1)所示的玻尔模型基态(n=1)时的德布罗意波长λ1。

同理可得R21的动量概率振幅：

(13)

则动量大小在p～p+dp范围内的概率为

(14)

可得德布罗意波长分布的概率密度为

(15)

在λ∈(0，∞)范围内，R21态的最概然德布罗意波长λp2=4πa0，等于玻尔模型第一激态(n=2)的德布罗意波长λ2。

最后，R32态的动量概率振幅：

(16)

动量大小在p～p+dp范围内的概率为

(17)

可得德布罗意波长分布的概率密度为

(18)

在λ∈(0，∞)范围内，R32态的最概然德布罗意波长λp3=6πa0，它等于玻尔模型第一激态(n=3)中电子的德布罗意波长λ3。

3 结论

综上所述，可得出结论，德布罗意对玻尔氢原子模型解释中的德布罗意波长在物理实质上对应于氢原子量子态中径向函数Rn(n-1)(即径向量子数nr=0)的最概然德布罗意波长。