流体力学概念性理解缺失的启示
2020-07-06王艺凝吕洪凤
王艺凝 张 豪 吕洪凤
(1中国农业大学烟台研究院,山东 烟台 264670; 2中国农业大学理学院, 北京 100083)
1 导出问题
流体包括气体、液体(生物液)、大气、海洋等。流体的平衡状态、运动状态以及流体和其他物体间的相互作用和规律是流体力学需要研究的内容。流体力学的知识点较多,既有静力学、动力学等高中学习过的经典力学的基础知识,又有流线、湍流等特定概念,不少内容对初学者相当有难度。很多学生在学习中对基础概念重视不够、理解不清,导致学习难度较大,从而影响教学进程和人才培育的质量。
A.Suarez等人从物理教育研究的视角,通过客观题、主观题、学生访谈等多种形式,系统地整理了学生在学习流体力学部分的困难,并指出导致这些学习困难的原因,从而为进一步设计有针对性的教学方法提供了参考[1]。为了摸清学生在理解、应用流体力学概念时的困难,本文参照A.Suarez等人在乌拉圭共和国大学的实验,对中国农业大学大一理工科学生进行了研究。希望可以通过比较独立教学情况,探究如何解决流体力学的概念理解困境。
2 研究过程及结果
A.Suarez等人评估了他所在学校6次测试中的600份试卷,依据错误率对理想流体力学相关的题目进行了归类,从而提出学生在该部分有概念性缺失的假设,为了验证该假设,遂构建了半结构性访谈类测试[1]。我们将该测试题目整理成单选题(详见附录),通过微信和PPT相结合的雨课堂在班级内发布。为分析学生对各题目相应知识点的掌握程度及出错原因,我们给出了各题的选项,见表1。
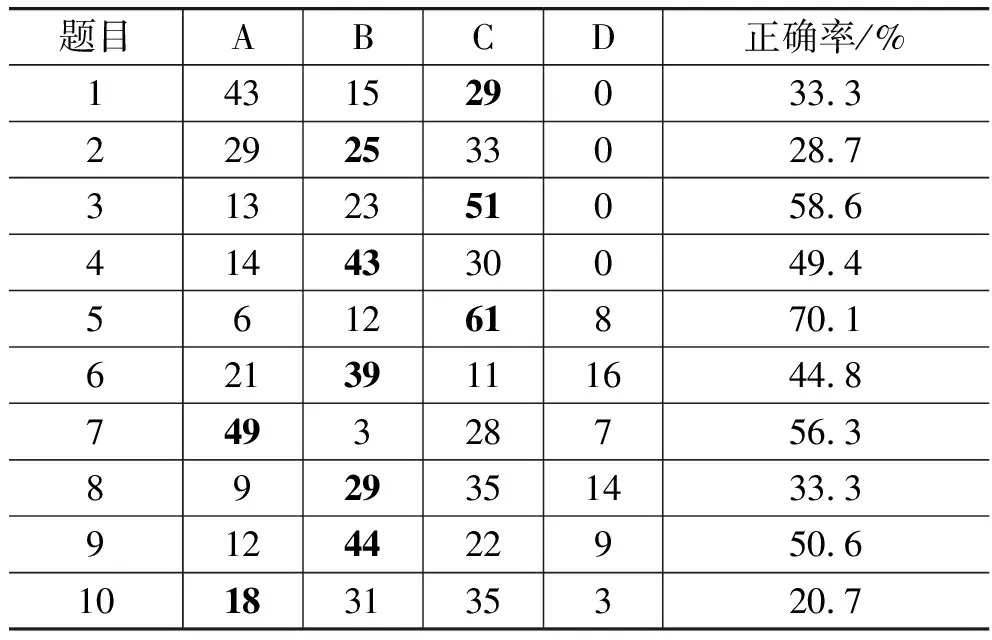
表1 答题选项分布(加黑体者为正确答案选项)
从表1可以看出,学生对1、2、8、10题的答题正确率偏低,数值≤1/3; 4、6题的答题正确率≤1/2;3、5、7、9题的答题正确率略高,属于1/2~3/4范围。经过对以上题目内容的分析,我们对学生的错题原因推测如下:
2.1 伯努利方程和连续性方程使用条件掌握不当(题目1和题目10)
1) 测试题1,正确率33%
(1) 正确解答:根据连续性方程,流体元(质点)在通过均匀截面的垂直管道下降时的速度是恒定的。
(2) 错误解答:流体加速运动(选项A)。近50%的学生沿用重力做功使物体加速的质点力学知识,而忽略了流体的特性、未考虑流体元彼此之间的相互作用。
2) 测试题10,正确率21%
(1) 正确解答:理想流体遇到障碍物、流线变形时,同一高度,流线曲率半径小处的压强小(pA>pB)。
(2) 错误解答:流线曲率半径小处压强大(选项B)、曲率不同处压强相同(选项C)。选项B和选项C的错选率相当,相当一部分学生沿用了流体静力学中同高度处压强相同的知识,未识别出流体元正在加速;也有一部分同学是应用伯努利方程失当。
2.2 流体静力学与动力学混淆不清(题目2和题目8)
1) 测试题2,正确率29%
(1) 正确解答:理想流体从大容器进入下端的窄小竖直管道时,流体在小管中的速度比容器中的快,进口处与小管内某点的压差应低于流体静压力差ρgΔh。
(2) 错误解答: 压差高于(选项A)、等于(选项C)流体静压力差。错选的学生多忽略了流体可流动的前提,受静力学的影响,认为压力只与液体顶部的液柱重量有关。
2) 测试题8,正确率33%
(1) 正确解答:理想流体从大容器进入下端的窄小竖直管道时,长度为dy的流体元在小管中受到的重力G和管壁表面作用力F相等。
(2) 错误解答: G

图1 中、乌两所高校对流体力学概念理解之比较
中、乌两所高校独立教学情况下所得到的结果比较见图1。由图1可知,乌方的学生表现普遍较好。这可能是由于中、乌两所高校在物理教学上的课时不同,导致了双方对流体力学概念的理解存在一定的差异。被研究的乌方大学物理课程为15周75学时,流体力学占用了3周15学时;中方大学的普通物理公共课为16周96学时,流体力学只占了2周6学时。两者的学习内容相仿,但在授课时间上差了2.5倍。此外,乌方第3、4、10题的正确率比中方低,尤其是第10题,乌方学生全部选择了在等高度处、弯曲流线压强处处相同的错误选项。这表明双方学生对伯努利方程的使用均有不同程度的滥用。从题目2和8可以看出,相较于乌方学生,中方学生在从流体静力学到流体动力学的过渡方面产生了不适感。题目3的正确解答是流体元在小管内压强处处相同,这和题目1流体元在小管内的速度处处相同是相洽的。乌方该题目的正确率比第一题的低是因为有部分学生因马虎错答;中方题目3正确率反倒比题目1和8高,则从另一侧面显现出很多同学没有前后题目一致考虑的全局观,也显示了概念应用的混乱性。
上述结果对大学物理流体力学板块的概念教学具有一定的启示性,提示我们在教与学的实践中应该关注以下几点:
1) 液体的不可压缩性
高中知识告诉我们,气体可以压缩而液体不可压缩。但学生们会认为液体在流过狭窄的管道时会被压缩[2]。如,浇花的水管口被捏扁时,喷出的水流速快,这使得学生认为高压应该对应高速。他们把压强等同了力,并将力和速度关联而不是与加速度关联。事实上,若不考虑高度变化,当液体流过的管道变窄时,由伯努利方程可知窄管处的液体流速大、压强低。
2) 伯努利方程的适用性
在运动学、质量守恒方程、能量守恒方程等质点模型中学习过的知识在流体力学中依然适用。流体中有流体元的概念,这也是流体连续介质模型提出的基础。流体元具有宏观物理量如质量、速度、密度等,这些物理量都是空间和时间的连续、可微函数,满足一定的物理定律。流体元速度的方向是流线的切线方向,速度场的空间分布及其随时间、空间的变化是流体力学的研究内容。伯努利方程就是没有“黏性”的理想流体元在流线围成的流管内的机械能守恒定律,只对可逆绝热过程的定熵流动适用。应用伯努利方程时,流体需要满足定常流动、不可压缩、无摩擦力等假设。
3) 流体静力学与流体动力学的关联
物体在平衡条件下的静力学可以看成是动力学的一个特例。对于静止流体,流线上各点的速度为零,由伯努利方程可以得到压强和高度之间的关系。这使得学生难以理解伯努利方程应用于同一流线上不同点之间的关系,很多同学认为静止液体与流动液体的压强应该是一样的,压强只与高度有关,压差来自于参考点上方的液体重量,从而混淆了静力学与动力学[3]。
在教学时,需关注学生掌握基本概念的程度,选择适当的讲授方法,如使用恰当的推导方式、做好必要的理论铺垫等[4]。在翻转课堂上,可以引入慕课等短视频,对知识点进行梳理和分解。此外,针对学生理解、应用流体力学概念的困难,有的放矢地设计、编写该部分的教学材料,也会对解决该问题有所改善。
3 结语
为了摸清学生在理解、应用流体力学概念时的困难,探究如何解决该困境,我们对中、乌两所高校独立教学情况下所得到的结果进行了比较研究。相对于高中的力学,大学的流体力学是全新的知识,流体元的特性与质点的特性既有关联又有不同。学生在该部分的学习难度大,影响了教学质量。许多学生能将伯努利方程应用于流体力学的解题过程,却没有考虑到该方程来自于一个守恒定律,作用于沿着流线移动或同一流管内的流体元。学生在熟练地调用连续性方程和伯努利方程解题时,并没有意识到压力梯度与空间速度变化相关。学生们很难理解运动中流体的不同部分如何相互作用,无法将运动学与动力学联系起来。以上概念误解和困难,在所研究的中、乌两高校学生中均存在。为了解决该问题,应适当地提高授课学时、在授课过程中改进讲授方法、设计有针对性的教学材料等。这对改善现阶段理工类本科教育有一定的借鉴参考意义。
附录题目:

图A1 排水管容器
1. 如图A1所示,一个高为h的容器装满水,水位h保持不变,忽略水的黏度,一个长为L的排水管(和出口处的直径相同)位于排水口处。 如果水从容器刚进入排水管时的速度为v, 在排水管中流动的速度会如何变化?
A. 变大 B. 变小 C. 不变
2. 接题1,考虑图A1中被标记的点1,2,3。点1在排水管上方,点2、3在排水管内。点1、2之间的压差Δp比ρ(z2-z1)的值________?
A. 更高 B. 更低 C. 相等
3. 接第2题, 图A1上2、3点间的压差Δp比ρg(z3-z2)________?
A. 更高 B.更低 C.相等
4. 假设在之前提到过的带管子容器旁放置一同样的容器,两个容器内有等量的水。新容器底端有同样的洞但没有排水管,如图A2所示。同时放水,哪个先排完?
A. 无管容器 B. 无管容器 C. 两者同时

图A2 两等量容器
5. 在一水面高h的箱底端有一长L的垂直管。忽略水的黏滞性。考虑管内的点A、点B以及管外的点C、点D(图A3),下面关于流速正确的是
A.vA
C.vC

图A3 箱底垂直管
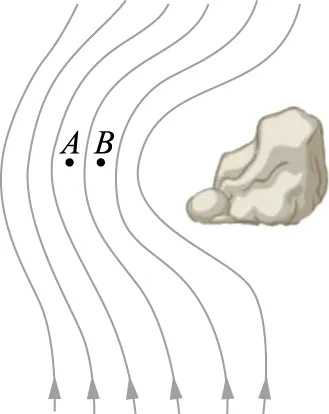
6. 接第5题, 下面关于压强正确的是?
A.pA C.pC 7. 以下哪种因素导致了管外“水流直径会随着流体的流出而减小”现象的产生?即,为何图A3上D点对应的横界面比C点对应的小? A. 流速 B. 装置结构 C. 空气阻力 D. 压力 图A4 流体元 8. 若以垂直管道内长度为dy的流体元为研究对象(图A4),已知其所受的两种力G(重力)和F(管壁表面作用力),以下对这两种力的大小描述正确的是? A.G C.G>FD. 无法确定 9. 接第8题,若以垂直管道外长度为dy的流体元为研究对象(图A4),该流体元受到的合力为? A. 0 B.其重力G C.空气压力 D.无法确定 10. 已知流动液体遇到障碍时,流线发生严重变形。流体元通过等高的A、B两点(图A5)时速度相等。试比较A、B两点的压强(假设压力梯度与速度变化之间没有联系) A.pA>pBB.pA C.pA=pBD. 无法确定 图A5 形变的流线