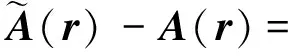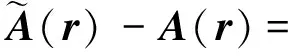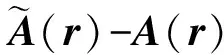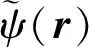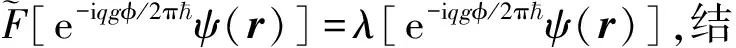磁单极狄拉克弦上磁场的显明形式
2020-07-06林琼桂
林琼桂
(中山大学物理学院,广东 广州 510275)
磁单极的存在(更严格地说是存在至少一种粒子其磁荷与电荷之比与其他粒子不同)导致的一个重要结论是电荷的量子化。仅这一点就足以令理论工作者着迷。磁单极从理论上提出[1]至今已经接近一个世纪,但一直未能在实验上观察到。尽管如此,由于理论上的魅力,它还是受到了持续而广泛的关注。
磁单极的磁场B类似于点电荷的电场,形式很简单。但是,为了将其纳入量子力学,人们必须找到一个矢量势A来描述它。另一方面,A的存在性是以方程·B=0为基础的。既然有了磁单极,后者便不再成立,于是A的存在性就有了疑问。如果一定要用A来描述,那么就难以避免A会具有某种奇性,狄拉克磁单极描述方案就是这样。或者,人们需要用两幅图(chart)构成的图册(atlas)来覆盖三维空间,然后在不同的图上采用不同的矢量势,在重叠区域,它们相差一个规范变换,这是吴大峻-杨振宁磁单极描述方案[2]。
具体来说,狄拉克的矢量势对应的磁场除了磁单极应有的平方反比场,还多了一条磁通弦(通俗地说就是一条磁力线),称为狄拉克弦。它从磁单极所在之处沿任意曲线通向无穷远处,其磁通量抵消了磁单极平方反比场的磁通量,使得任一闭合曲面的磁通量仍然为零。只有当磁通弦没有物理效应(至少对于所考虑的问题)时,这样的矢量势才是对磁单极的恰当描述。讨论磁通弦是否有或对于哪些问题有物理效应,超出了作者的学识,也远远超出这篇小文的范围。前述关于磁通弦的性质在文献上一般只有文字描述,这些性质可以通过考察矢量势的环路积分而得出。但是对矢量势微分(取旋度)并不能自然得出与磁通弦对应的磁场项。当然人们可以利用前述性质手动构造并写下该磁场项,但是这难免有斧凿之嫌。本文将矢量势写成积分形式,然后通过微分运算自然得出包含磁通弦项显明形式的结果。上述矢量势的积分形式在文献上并不陌生[3,4],文献[3]也作了微分运算,但是没有得出磁通弦项的显明形式。对于具有不同狄拉克弦的矢量势之间的规范变换,我们作了一些评述,并指出过去论证电荷量子化的一种方法存在漏洞。最后简单介绍了吴大峻-杨振宁磁单极描述方案,并简述该方案中电荷量子化的论证思路(吴-杨原文[2]对此论证并无详细说明)。希望本文对于电动力学的初学者有所帮助,对于教师也有一些参考价值。
1 狄拉克弦上磁场的显明形式
设磁单极的磁荷为g,位于坐标原点,狄拉克矢量势为

(1)
本文同时采用直角坐标和球坐标,在后面一个实例计算中也采用柱坐标,所用符号都是熟知的,eφ、ez等是单位矢量。对上式取旋度,只能得出磁单极磁场
(2)
而得不到实际存在的磁通弦项。实际上,A(r)在θ=π处有奇性,微分运算在这些地方是有疑问的,可能把某些东西弄丢了。这类似于在球坐标中计算2(1/r),并不能直接得出δ函数。上式的一个显然的推广是
(3)
其中e是任意给定的单位矢量。对上式取旋度,得到的同样是Bg(r)。
现在我们把式(3)改写成下述积分形式
(4)
考虑沿e方向的直线从无穷远至原点的极细螺线管,有助于找到这个积分表示[3,4]。然而,在数学上,这不是必须的。我们只需要证明上式的积分结果是式(3)即可。为此,令u=-s,将上式化为
(5)
分解r+ue=[r-(r·e)e]+(u+r·e)e,两部分互相正交,由此易得
(r+ue)2=r2-(r·e)2+(u+r·e)2
(6)
于是
(7)
利用积分公式
b>0 (8)
完成上式的积分,结果就是式(3)。这就证明了式(4)是式(3)的积分表示。
式(4)可以改写为
(9)
(10)
B(r)=Bg(r)+B′(r)
(11)
其中

(12)
就是磁通弦项的显明形式。如果e=ez,则很容易求出积分,而得
B′(r)=ezgδ(x)δ(y)θ(-z)
(13)
其中θ(-z)是亥维赛(Heaviside)阶跃函数,这是沿z轴负半轴由原点伸展至无穷远的磁通弦,磁场沿z方向,磁通量为g。值得指出,如果我们先计算半径为a的半无界圆柱螺线管的磁场,然后令a→0(同时让I→∞以保持μ0πa2I=g固定,其中I是单位长度的电流),得到的磁场正是上述结果,而磁通弦对应于螺线管内的磁场。详细讨论需要较多篇幅,从略。
下面进一步推广式(4)。考虑一条空间曲线L,它由定点r0伸展至无穷远,其参数方程为
r=r(s), -∞ (14a) 满足 r(-∞)=∞,r(0)=r0 (14b) 我们选取参数s使得ds=|dr(s)|,那么切矢量 (15) 是单位矢量,指向参数增加的方向。参数s类似于古典微分几何中的弧长参数,后者是一个内禀参数,并使得切矢量是单位矢量[5],不同之处是我们的参数s是负的,这是因为我们要把r0当作曲线的终点而不是起点。今构造矢量势 (16) 相应的磁场是 (17) 注意到e(s)·[1/|r-r(s)|]=-(d/ds)[1/|r-r(s)|],上式的计算与式(10)完全类似。最终得到 B(r)=Bg(r,r0)+B′(r) (18) 其中 (19) 显然,Bg(r,r0)是位于r0处的磁单极产生的磁场,而B′(r)是沿曲线L的磁通弦。因此,矢量势(16)描述的是狄拉克弦为曲线L的磁单极。当r(s)=se,则L是沿e方向的直线,此时r0=0,e(s)=e,以上结果就退化为式(11-12)。 举一个实例。设L是圆柱螺线 (20) 则r0=exa,切矢量为 e(s)=-exωasinωs+eyωacosωs+ezωb (21) 代入式(19),即可写出B′(r)的形式。但是这个结果不太直观。如果采用柱坐标,则可将各分量写成 (22) 这样物理图像就非常清晰了。对于B′φ(r),考虑ρz半平面且z<0,可以看到磁通弦多次穿过该半平面(注意φ和z的取值范围都是(-∞,0]),每次穿过的磁通量都是g。对于B′z(r),考虑z给定且z<0的平面,可以看到磁通弦在ρ=a,φ=z/b处穿过该平面,磁通量也是g。 (23) 其中n′是S上r′处的法向单位矢量,dσ′是面积元,而 (24) 是S对r点张开的立体角。下面对这个结果作一些讨论。 对于式(23)中的第二项,当r在S附近时,我们可以以S上靠近r的某点为原点引入局部直角坐标系,完成切向坐标的积分可得该项结果为gδ(xn)n=[gε(xn)/2],其中xn是局部直角坐标的法向分量,ε(xn)是符号函数。所以在S附近,我们可以局部地写出 (25) 当r越过S时,两项的跃变正好互相抵消了,因此整个规范变换函数Λ(r)本身并没有跃变。由此可见,上一段的论证确实存在失察之处。当然,这绝不意味着电荷量子化的结论不成立,因为可以有其他论证方法,比如吴大峻-杨振宁磁单极描述方案中的论证方法,后面会加以讨论。 (26) 其中e′是与e垂直的任一单位矢量。特别地,如果e=ez,取e′=ex,则得 (27) (28) 利用积分公式(8)完成对z′的积分,然后对x′的积分也很容易计算,最后得出 -π<φ<π (29) 第二个等号很容易验证。代入式(23)(忽略第二项),所得结果与式(27)一致,如所期望。不过,对于更一般的曲线,计算立体角的显式是相当困难的。 (30) 相应地,波函数满足 (31) (32)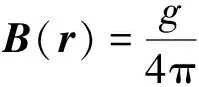
2 规范变换与电荷量子化