高超声速飞行器电离反应流场特性研究

卫丽云,王学德

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

随着人类对高空稀薄流领域探索的不断深入,高超声速飞行器的性能和用途也得到了极大的改善,尤其在军事方面,高超声速飞行器得到了全面发展,比如,高超声速飞行器能有效地进行高空预警,侦查和高空打击工作,极大地拓宽了作战空间。为此,高超声速飞行器水平已逐渐成为各国军事实力的表现。但随着飞行条件的不断升高,稀薄气体电离成为高超声速飞行器不得不考虑的问题,由其导致的“黑障现象”[1]很大程度上影响了再入飞行器与地面的通信交流,且电离反应的吸放热也会影响流场中飞行器的气动特性。而对于电离反应流场的研究,必须在非电离反应流场的基础上引入新的组分,即非电离流场五组分所对应的离子和游离电子。离子和电子的加入使流场中的能量分配产生新的变化,且因为反应机理的不同,电离反应的实现方法也一直是研究的热点。

直接模拟蒙特卡罗方法(DSMC)是一种基于统计学的数值模拟方法,该方法自提出以来被广泛应用于稀薄流问题的研究[2-3]。将电离反应引入DSMC一直以来被视为最可能的研究电离反应的途径。早期的研究大多将电离反应几率与Arrhenius 速率系数函数相关联,而Arrhenius速率函数依赖于单温度速率常数的宏观信息,且建立在化学反应平衡的假设上,这一思想在文献[4-5]中都有应用。但是电离反应温度可达上万开尔文,目前并没有如此高温下完备的单温度速率数据,因此,在这一温度范围内,宏观单温度速率常数并不适用。尽管文献[6]在此基础上引入振动能的影响,使这种方法更接近真实效应,但对电离反应发生的几率的处理依旧依赖于气体的宏观性质。BIRD[7]提出了一种基于量子动力学的模型—Q-K模型,该方法摆脱了对宏观速率方程和气体平衡假设的依赖,将所有的反应与微观粒子的振动能相关联。但由于电离反应的特殊性,主导电离反应发生的往往不是粒子的振动能的激发,而是相对应的电子能的激发,因此,仅考虑粒子振动能的Q-K模型并不完全适用于电离反应。LIECHTY等[8]基于粒子微观动力学理论,将电子能级引入电离反应模型,认为电子能在流场中的计算应该包括3个部分:电子能作为电离反应碰撞能的一部分,必须从能量分布中取值;电子能在粒子碰撞的过程中也需和其他能量一样,有合理的分配过程;电子能的产生和消耗必须有合理的转换速率。

由于研究采用模型的局限性或者研究的侧重点不同,学者们在程序中考虑的电离反应也不尽相同。LIECHTY等[9]应用分子动力学原理将联合电离反应和置换电离反应引入DSMC程序中,重点研究了将这一方法用于计算极高温度下的速率常数的可能性。SHEVYRIN等[10]根据流场电中性假设,不将电子作为粒子进行模拟,直接把网格离子数密度之和作为电子数密度。这一方法虽然简化了程序,但直接忽略了电子与原子碰撞发生的电子激发电离反应。FANG等[11]采用不同的权重因子将中性粒子与带电粒子进行区分,重点考虑了含有电子参与的电离反应,忽略了包含电荷转移的置换电离反应。

本文从分子动力学理论出发,将电离反应分类进一步细化,考虑更多的电离反应,并根据电离反应发生机理的不同采用不同的反应发生判据。首先通过对RAMC-Ⅱ外形的飞行器的飞行模拟,验证了本文所采用二维轴对称电离程序的有效性。随后又应用这一模型,研究了电离反应流场与非电离反应流场的不同以及不同种类电离反应对稀薄流场飞行器特性的影响程度。

1 电离反应及实现方法

1.1 电子激发能的计算

在电离反应中,伴随着电子的产生或转移,粒子的电子态受到相应的激发,会产生一部分能量,定义为电子激发能。电子激发态从相应的碰撞实效温度(由碰撞中分子的相对平动能和电子能之和求得)的平衡态取样得到,而一个粒子的电子激发能由下式计算得到:

Ee=∑(Nj/N)ej

(1)

式中:ej为电子能级j的能量,Nj为能级j中的粒子数,N为总粒子数,Nj/N可以根据平衡分布得出,如下式所示:

(2)

式中:k为玻尔兹曼常数;T为碰撞实效温度,由碰撞对粒子的碰撞数量平衡分布取样而得;gj为能级的简并度,具体的gj和ej的值可参考文献[4]。

1.2 电离反应的DSMC实现

根据电离反应发生机理的不同,电离反应大概可分为3类:联合电离反应、电子激发电离反应、置换电离反应。其中,置换电离反应因为发生置换的粒子的种类不同,起主导作用的能量形式会有相应的变化,可进一步分为电子交换电离反应和含离子的置换反应两类。

联合电离反应的过程可以看做两步反应,如式(3)所示,其中e代表电子。第一步反应和复合反应相似,生成的AB*可以看作络合物,极不稳定。第二步反应中,反应初始的碰撞能应该包括离解能,再根据L-B振动松弛理论进行能量分配后,若此时AB*的平动能和电子激发能之和大于其电离活化能,则联合电离反应发生。本文所考虑的联合电离反应如式(4)～式(6)所示。

A+B→AB*→AB++e

(3)

(4)

(5)

N+O→NO++e

(6)

电子激发电离是单原子分子和电子碰撞生成离子的反应,其一般反应式可以写为式(7)的形式。其中电子没有电子激发能,碰撞对的碰撞总能记为碰撞对的相对平动能和单原子分子的电子激发能之和。该类电离反应是否发生主要取决于碰撞能与电离活化能的相对大小,当该碰撞对的碰撞能大于单原子分子的电离活化能时,电子激发电离反应发生。本文所考虑的电子激发电离反应如式(8)～式(9)所示。

A+e→A++e+e

(7)

N+e→N++e+e

(8)

O+e→O++e+e

(9)

置换电离反应是由一个离子和一个中性粒子碰撞而发生的反应。根据反应机理又可细分为2类,这里称两粒子间碰撞得失电子的反应为电子交换电离反应,而两粒子间碰撞得失原子的反应为含离子的置换反应。

电子交换电离反应的过程可以看作中性粒子受电子态激发失去电子,之后由于电荷间的相互作用,离子得到电子,其一般式可写为式(10)。对于这类化学反应中的吸热反应,采用L-B振动松弛理论进行能量分配后,若此时中性粒子A的电子能级仍大于反应的活化电子能级,则反应发生。而对于这类反应中的放热反应,判据与吸热反应相同,只是在进行能量分配时,除了本身的碰撞总能外,还需考虑反应能。本文所考虑的电子交换电离反应如式(11)～式(14)所示。

A+B+→A++B

(10)

(11)

(12)

(13)

N+NO+N++NO

(14)

对于含离子的置换反应,其一般式可写为式(15)。这类化学反应与中性粒子的置换反应机理类似,当碰撞对的碰撞总能达到一定值,双原子粒子的化学键发生断裂,其中一个原子会与碰撞对中另一反应原子结合,发生置换电离反应。所以,对于这一类化学反应,主要的影响因素还是双原子粒子的振动能级。对于吸热反应,对碰撞能采用L-B振动松弛理论进行能量分配,若此时双原子粒子的振动能级仍高于反应的活化振动能级,则反应发生。而对于放热反应,在进行能量分配时需考虑碰撞能和反应能的总和,之后若反应生成的中性粒子的振动能级高于活化能级,则反应发生。本文所考虑的含离子的置换反应如式(16)～式(19)所示。

A+BC+→AB(AB+)+C+(C)

(15)

N+NO+N2+O+

(16)

(17)

(18)

NO+O+O2+N+

(19)

2 计算方法

2.1 DSMC简介

稀薄流领域的非连续性导致N-S方程失效,基于N-S方程的数值模拟方法也就不再适用于该领域问题的研究,BIRD提出的基于Boltzmann方程的DSMC方法成为目前研究稀薄流领域问题最常用的方法。该方法通过对Boltzmann方程所描述物理过程的模拟,将粒子的运动和碰撞解耦,解决了Boltzmann方程碰撞项难解的问题,用一个模拟粒子代表一定数量的真实粒子,各模拟粒子之间以及模拟粒子与物面之间不断进行着能量交换,最后通过采样统计得到计算域内计算网格的宏观特性分布。

2.2 轴对称流场的DSMC实现方法

二维的DSMC程序由于忽略了z方向的粒子运动,计算结果会与实际情况有较大的偏差,但是三维的DSMC程序又会极大地增加计算难度,降低计算效率。因此,本文引入二维轴对称程序[12],将z方向的运动并入y方向,提高二维程序计算精度的同时没有增加很大的计算量。

将z方向的运动叠加到y方向,实际上就是将Oyz面内的运动作极坐标转化,程序中的粒子位置的y坐标取Oyz面的极坐标值,相应的Δt时间内y坐标的变动也需考虑y和z2个方向上的运动。

此外,作轴对称处理后沿网格体积径向方向变化较大,而DSMC程序中的碰撞取样是按网格体积均分取样的,这就会导致网格取样不均的问题,当靠近轴线的网格达到计算要求的取样数时,外围的网格取样数会过多,极大地提高了计算难度。在此引入半径权重系数WF,设定一个参考半径RF,RF的取值要比网格平均尺寸小得多。WF的定义为

WF=r/RF

(20)

式中:r为粒子所处半径,即粒子的y坐标;WF的值最小取1。网格内的每个模拟粒子所代表的真实粒子的数量由原来的F变为WFF,这样大大减小了外围网格与靠近轴线网格之间粒子分布数量的差值,取样数量也得到平均。

2.3 电子运动在DSMC中的实现方法

电子运动的处理也是电离反应的一大难点。电子的质量为9.11×10-31kg,相较于流场中的其他重离子,电子要轻大约5个数量级,而粒子的热运动速度与粒子质量的平方根成反比[13],这就表示电子的运动速度要比其他重粒子快大约2个数量级。在适合捕捉其他粒子运动的时间步长内,无法准确跟踪电子运动,但若以电子的运动速度取时间步长,又极大地提高了DSMC计算的难度。

目前处理电子的运动主要有3种思路:①人为增大电子质量3个数量级[4];②捆绑法[14];③平均速度法[15]。这3种方法都可以满足流场基本电中性的假设,且在国内外均有应用。

本文采用以上的第一种方法,人为增大电子质量,将电子质量认为是9.11×10-28kg。为了保证碰撞过程的质量守恒,必须同时改变离子的质量。因为即使电子的质量增大3个数量级,还是比离子的质量小大约2个数量级,占离子质量的比重很小,若将离子质量减少相应比重,对其热运动速度的影响很小,可忽略不计。表1为离子质量改变的详细信息。

3 验证算例

3.1 程序有效性验证

本文的验证模型取RAMC-Ⅱ试验中采用的飞行器外形,具体的尺寸如图1所示。沿机身方向分别布置了4个微型反射器,微型反射器用于测量所在位置垂直物面方向的最大电子密度,具体的位置也在图1中标出。计算条件取自文献[10],如表2所示。

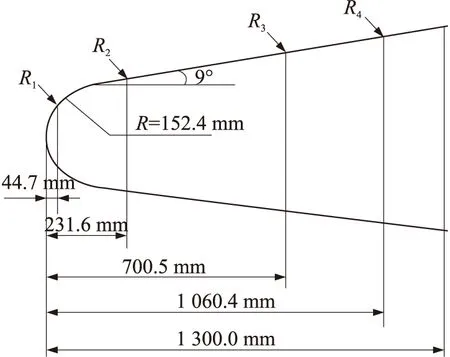
图1 RAMC-Ⅱ试验中飞行器外形及探测点分布

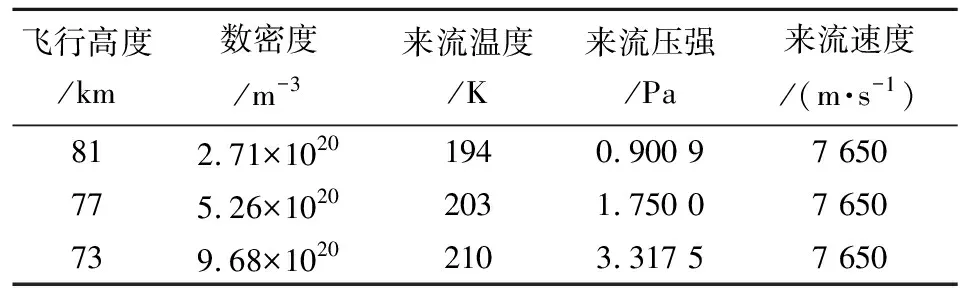
表2 计算条件

本文的网格采用非结构贴体网格,分子碰撞采用VHS(变径硬球)模型,碰撞能量分配采用Larsen-Borgnakke模型,分子与物面相互作用采用完全漫反射模型,物面温度设置为恒温1 000 K。由于飞行器的攻角为0°,只计算一半流场。

图2为不同高度(H)下得到的飞行器周围密度云图。飞行器头部有很明显的弓形激波,激波后的气体密度急剧增大,且随着飞行高度的增加,流场的密度逐渐减小。

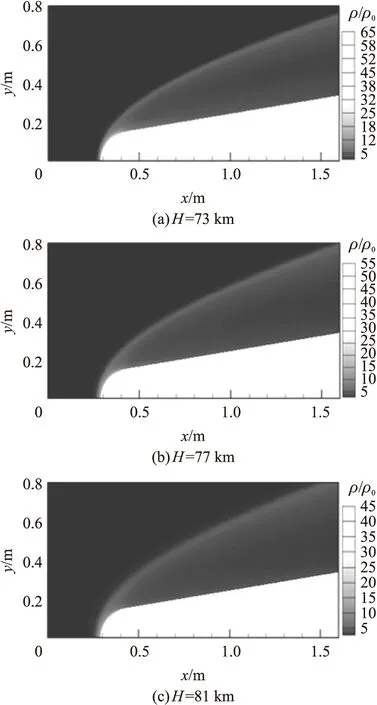
图2 不同高度流场密度云图

图3为不同高度下飞行器周围温度云图。激波后的气体温度迅速升高,但沿贴近壁面方向温度逐渐降低。随着飞行高度的升高,激波的厚度有所增加。以上密度和温度云图的变化趋势与文献[16]一致(二者的计算条件相差不大),从定性角度分析,所采用的电离程序是符合变化规律的。

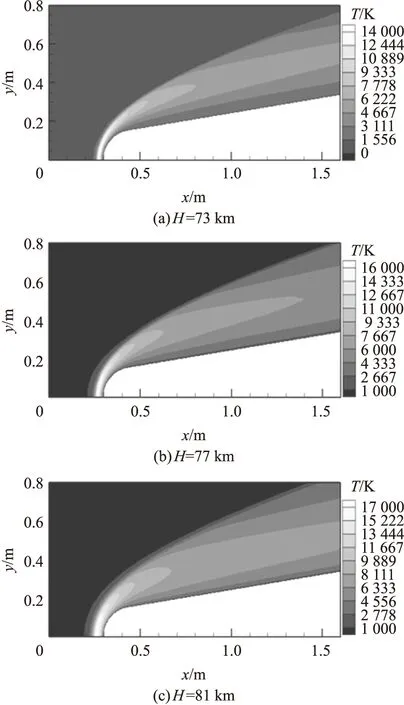
图3 不同高度流场温度云图

图4为不同探测点(已在图1中标出)垂直于物面方向上的最大电子数密度随飞行高度变化的对比。图中,H为飞行器运行的海拔高度,ne为垂直物面方向上的最大电子数密度,对ne取对数,即lgne。由于DSMC中统计是以网格单元为单位,而在粒子运动过程中,各网格中的粒子数会不断发生变化,取样数也会发生相应的变化,造成统计过程中存在一定的涨落误差,一般认为,电子密度计算误差允许在3倍以内[17]。从图中可以看出,无论哪一探测点,本文所采用的程序得到的计算结果基本与文献[10]的结果以及实验数据处于同一数量级,就相差倍数来说,与文献[10]之间的差距更小一些,具有良好的一致性。这就从定量的角度说明本文所采用电离程序的正确性。

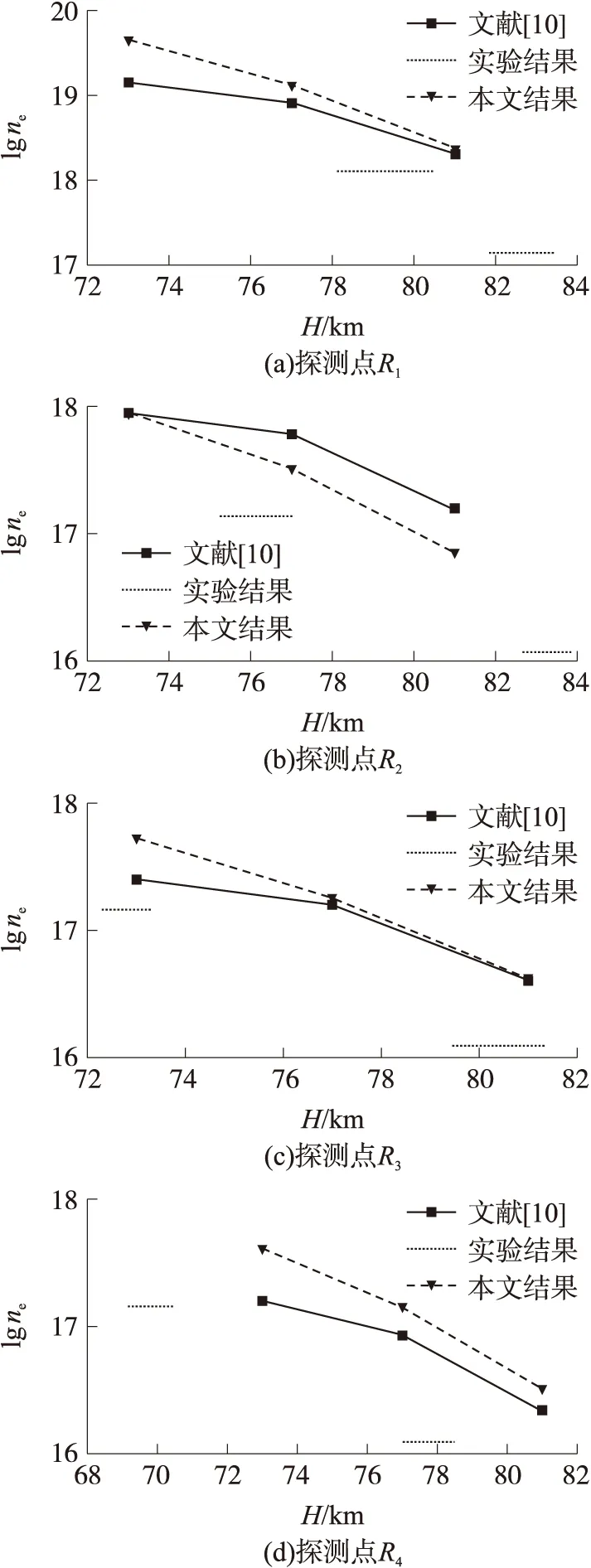
图4 不同探测点的最大电子数密度

3.2 网格无关性验证

在DSMC中,网格主要起2种作用:①对宏观流场性质进行空间离散,便于统计流场信息;②便于分子碰撞对的选择。网格尺寸过大,会造成流场宏观特性的估计误差增大;网格尺寸过小又会极大地增加程序的计算量,降低工作效率。因此,合理的网格设计对DSMC计算结果的可信度有重要影响。对于网格尺寸的选择,学者们采用的标准不一,但原则上最大不超过来流分子的平均自由程。本文引入一个无量纲参数Z:

(21)

式中:s为网格单元的平均尺寸,λ为来流分子平均自由程,Kn为来流的克努森数,L为流场特征长度。

以90 km飞行高度条件为例,采用非结构贴体网格,取Z=0.33,Z=0.50,Z=0.80,Z=1.00分别计算了飞行器附近流场的特性。Z值越大,网格单元平均尺寸与分子自由程越相近,网格分布也就越稀疏。图5为不同网格密度下物面附近流场特性对比。图中,Cp为物面压力系数,CF为物面阻力系数,q为物面热流密度。为了方便比较,将横坐标x作无量纲化处理,此处的流场特征长度L取飞行器的模拟长度。

从图5中可以看出,4种不同尺寸的网格计算得到的结果吻合较高,特别是从物面压力系数分布和热流密度分布来看,这4种尺度的网格得到的结果几乎一致。但从摩阻系数分布来看,不同网格尺寸得到的摩阻系数峰值稍有不同,其中Z=0.50和Z=0.80两种网格得到的计算结果始终保持较高的吻合度,同时为了减小计算量,本文以下的计算中,统一采用Z=0.80的网格,即网格的平均尺寸取为来流分子平均自由程的4/5。

4 电离反应对流场的影响

4.1 电离流场特性

为了方便看出电离反应的影响,将5组分化学反应程序与11组分含电离的化学反应程序得到的计算结果进行对比,飞行条件取80 km海拔处的来流条件,如表3所示。

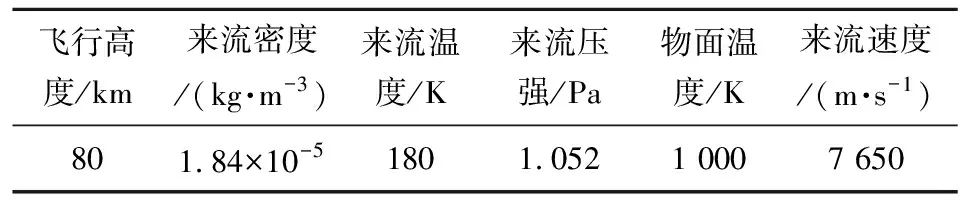
表3 来流条件

图6为80 km飞行高度下不同组分流场的温度对比。

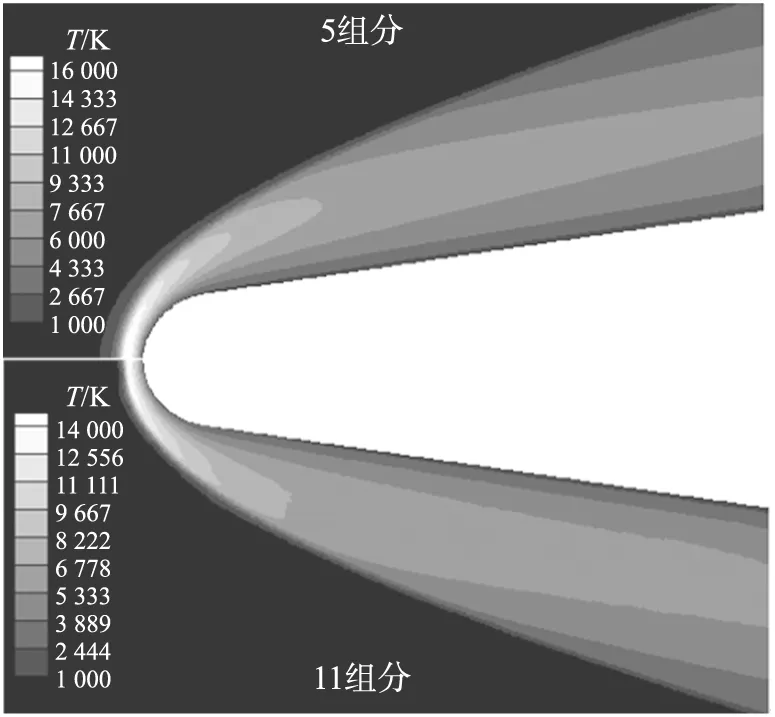
图6 不同组分下流场温度云图

可以看出,11组分流场的整体温度要比5组分低,其中5组分温度场的最大值为16 989 K,而11组分为14 380 K,相差2 500 K左右。从激波位置来看,11组分流场中的激波更靠近壁面,更薄一些。这是因为在本文的研究中,11组分与5组分相比,多考虑了21个电离反应,而电离反应的活化能与非电离反应相比较高,要使化学反应充分发生且达到平衡所需消耗的热量也就较大,也就会使11组分流场整体温度有所下降。基于流场中气体的热胀冷缩效应,在相同的壁面温度下,温度较低的流场的压缩性更强一些,以致11组分流场中的气体在壁面附近受到更大的压缩,形成的激波厚度也就相对较薄。

图7为80 km飞行高度下不同组分流场中的物面气动特性对比,x/R为流场横坐标与飞行器头部半径的比值。由图可知,物面压力系数的变化趋势不随流场组分的变化而变化,都是在驻点区域达到最大值,后沿x轴方向急剧下降,直到飞行器肩部位置后趋于平稳。而物面摩阻系数在驻点附近最小,之后急剧升高,到x/R约等于0.2附近达到峰值,之后的变化趋势同压力系数相似,快速下降到肩部附近后趋于平稳,且不同组分流场相差不大。由此可以得出,电离反应对飞行器表面的气动特性影响不大。壁面压力系数和摩阻系数分别取决于物面入射分子与反射分子的法向动量差和切向动量差,在相同来流条件下,虽然中性粒子在物面附近有可能电离产生对应的离子和电子,使飞行器周围的粒子数密度有所增大,但电子质量较小,即使本文将电子质量人为增大1 000倍,仍与重粒子相差2个数量级,因此电子对物面附近入射分子与反射分子的动量影响不大,因而会出现图7所示的情况。

图7 80 km飞行高度下不同组分流场物面气动特性变化

图8为80 km飞行高度下不同组分流场中物面热流密度对比。与气动特性曲线一样,不同组分流场的沿物面热流密度变化趋势一致,但5组分流场中的热流密度峰值明显高于11组分流场中的热流密度峰值,这是因为电离反应大多是吸热反应,会吸收大量热量,从而使飞行器表面与周围气体的热量交换减少。而这一差别主要体现在驻点附近,这是因为电离反应大多集中在驻点附近。电离反应的发生主要是因为高温下电子能态的激发,从图6可以看出,驻点附近温度是流场中的高温集中区域,因而发生的电离反应数量也就较多。

图8 80 km飞行高度下不同组分流场物面热流密度变化

4.2 不同电离反应对流场的影响

为了研究本文所考虑的3种电离反应的主次关系,依次将3种电离反应从程序中抹去,计算了这3种情况下的流场特性。飞行高度取为80 km,其他计算条件与表3相同。

本文来流速度为7 650 m/s,对应所含的能量大约为9 eV,根据文献[13],此时空气中产生的主导电离反应主要为联合电离反应。从本文所考虑的所有电离反应式来看,其他有带电粒子参与的电离反应的发生都是以联合电离反应产生为前提的。因而如果不考虑联合电离反应,则其他电离反应也不发生,计算得到的结果同5组分流场的计算结果相近,在以下的讨论中不作赘述。为方便叙述,将考虑所有电离反应的计算称为工况1,不计电子激发电离反应的计算称为工况2,不计置换电离反应的计算称为工况3。由前面的讨论可知,电离反应对飞行器表面气动特性的影响不是很大,所以后续讨论的重点为不同电离反应对电子密度及飞行器表面气动热的影响。

图9为3种不同工况下计算所得的飞行器头部电子密度的对比图。由图9可知,工况1和工况3的电子密度分布很相近,工况2的电子层相对较薄,密度也就小,不过3种工况的电子密度基本还在一个数量级上。从化学平衡的角度出发,若将电子激发电离反应从程序中抹去,即只考虑置换电离反应和联合电离反应,根据比较结果可以看出,置换电离反应对生成游离电子的联合电离反应有抑制作用,从而使流场中的电子密度有所降低,这是因为虽然置换电离反应会消耗一部分联合电离反应所生成的离子,看似会促进联合电离反应的正向发生,但由于置换电离反应较多,生成的离子种类也多,有的离子生成物与联合电离反应的离子生成物相同,一定程度上依然会抑制联合电离反应的正向发生,从计算结果来看,置换电离反应的抑制作用比促进作用大。若将置换电离反应从程序中抹去,即只考虑电子激发电离反应和联合电离反应,可以看到流场的电子密度整体偏大。这是因为电子激发电离反应消耗联合电离反应生成的游离电子的同时不会产生与其相同的离子产物,对联合电离的发生只有促进作用;另一方面,除去置换反应也使联合电离反应受到的抑制作用有所减弱。

图9 电子数密度对比(单位:m-3)

图10为不同工况下沿x方向探测点的垂直方向上的最大电子数密度比较。从图中可以看出,电子密度沿x轴方向逐渐减小,这与沿x轴温度逐渐降低,反应数减少有关。从3条曲线两两之间的差值来看,工况2下的电子数密度始终最小,工况3下的电子数密度始终最大,与密度云图所展示的差别一致,且工况2与工况1之间的差距比工况3与工况1之间的差距大。由此可以得出结论,本文所考虑的置换电离反应对联合电离反应的抑制作用比电子激发电离反应对联合电离反应的促进作用更明显。

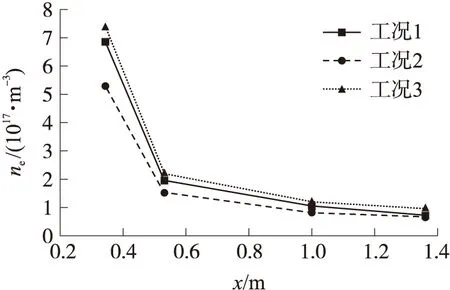
图10 不同探测点垂直方向上的最大电子数密度

图11为3种工况下飞行器头部热流密度的分布情况。无论抹去哪种电离反应都会使物面的热流密度有所升高,这种差距沿x轴方向逐渐减小,到飞行器肩部以后基本重合。因为电离反应大多是吸热反应,抹去其中一种电离反应都会使电离反应发生次数减少,从而减小了气动热在电离反应上的耗散,但由于在80 km处空气较为稀薄,总的电离反应数本来就小,所以会出现图11中工况2和工况3的热流密度虽有提升但差距不大的情况。

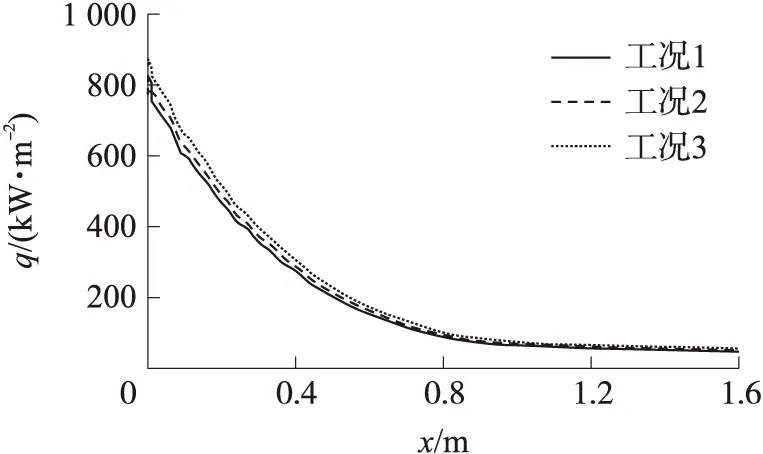
图11 不同工况飞行器头部热流密度的分布

从定量的角度分析,3种工况下物面最大热流密度保持在同一数量级,其中,工况2的物面最大热流密度为825 kW/m2,工况3的物面最大热流密度为870 kW/m2,以工况1为参照进行比较,差值百分比分别为4.43%和10.13%,也就是说,抹去任一种电离反应带来的热流密度变动不超过11%,其中抹去电子激发电离反应对热流密度的的影响尤其小。表明电子激发电离反应消耗的热量较少,这是因为本文所考虑的电子激发电离反应都为单原子分子与电子的反应,单原子分子本身的电离活化能就比双原子分子的低,因而反应所需吸收的热量也就较小。

5 结束语

本文从电离反应发生机理出发,对不同电离反应采用不同反应发生判据,采用人为增大电子质量1 000倍的方法处理电子运动,计算了高超声速稀薄流域的二维轴对称流场,研究了电离反应对高超声速飞行器流场特性的影响以及不同种类电离反应对流场的影响,结论如下:

①通过模拟RAMC-Ⅱ试验中飞行器的高空运行情况,验证了本文所采用电离模块的正确性,表明从分子动力学角度出发考虑电离反应是可行的。

②相同飞行高度下,与只考虑非电离反应的情况对比,考虑电离反应会使流场温度整体下降,激波厚度变薄,飞行器表面的热流密度也会有所降低,但电离反应对高超声速下飞行器表面气动特性没有明显的影响。

③联合电离反应是所有电离反应的基础,是生成游离电子的主要反应,本文所考虑的置换电离反应对稀薄流流场游离电子的生成有抑制作用,而电子激发电离反应对游离电子的生成有促进作用,且置换电离反应的抑制作用比电子激发电离反应的促进作用更明显。置换反应和电子激发电离反应均会使流场的热流密度峰值减小,但影响不超过11%,其中电子激发电离反应的影响尤其小。