样例设计的心理学研究及其对小学数学教学的启示
2020-07-04朱梦喻平
朱梦 喻平


【编者按】南京师范大学数学科学学院、南京师范大学课程与教学研究所喻平教授与他的合作者尝试梳理当代心理学关于数学学习的最新研究成果,并依据这些研究中的实验干预因素、手段或结论,提出一些针对某些专题领域的教学策略,希望能给一线教师的数学教学提供参考。接着2019年第6期,本期《前沿论坛》栏目继续与大家分享他们的研究成果。
摘要:心理学关于学习样例设计的研究,涉及样例的不完整设计、渐减提示设计、解释法设计、步骤编码设计以及多重样例的呈现方式设计等。将这些研究的成果应用于小学数学教学,可以得到的教学策略有:提供搭建完整样例的“脚手架”,设置样例的解释提示语和子目标提示语,组织样例的同型题和远迁移题,将样例与练习交互呈现等。
关键词:样例设计 小学数学 渐减提示 步骤编码 同型题
样例学习是观察、思考样例,并掌握样例中包含的规则,或从中习得新知识的过程。在类比迁移中,样例学习指先学样例(源题),再解决问题(靶题);样例起着引导抽象原则解决问题的重要作用。
数学教学的一个显著特征是,学生学习了概念、原理之后,教师要为其提供需要利用这个概念或原理解决的例题,让其通过这些样例的学习理解概念或原理。那么,如何选择例题?如何设计例题?一般说来,教师主要依据教材的例题。其实,照本宣科式的例题讲解是远远不够的。教学中,教师要思考:什么样的例题才能使学生对知识有深度的理解?例题的数量应怎样把控?例题的结构应如何设计?例题的顺序应如何安排?实际上,心理学关于样例设计已经有了许多研究,这些研究的结果特别是实验干预手段,都值得借鉴甚至直接应用于教学。
一、心理学关于样例设计的一些研究
样例设计的研究丰富多彩,主要是探讨不同的设计对学习效果产生的影响。研究主要基于实证,多是通过实验干预观察因变量的变化,从而发现一些规律性的事实。
(一)样例的不完整设计
不完整样例是指,删除样例中的一些解题步骤,要求被试报告出删除的解题步骤,然后对被试报告的答案给予反馈,即告诉被试正确的答案。而完整样例则是指,样例中的解题步骤是完整的,即给出完整的解题步骤和解题依据。此外,“不完整样例—分类”是指,呈现不完整样例,要求被试先对样例进行分类,再学习样例。
Stark对不完整样例的作用进行了研究。他设计了一个实验:实验组学习不完整样例,控制组学习完整样例。在实验组,用问号代替部分解题步骤,让被试发现缺失的解题步骤,然后给被试呈现完整的解题步骤。结果表明,与控制组相比,实验组被试的自我解释质量较高,获得了问题解决方法的迁移。
林洪新等人对180名小学六年级学生用样例学习两种代数运算规则进行了实验研究。结果显示,在无反馈的情况下,完整样例的学习效果好于所有不完整样例;在有反馈的情况下,只删除一个运算步骤的不完整样例的学习效果好于完整样例。这说明,反馈对不完整样例的学习有促进作用;在不完整样例的学习中,如果不对学习者进行及时反馈,那么学习的效果是不好的。这与Stark的研究结果是吻合的,因为Stark的研究是给实验组及时呈现完整解题步骤的反馈。
张奇等人对270名小学三至五年级学生用样例学习“去括号”运算规则进行了实验研究。结果显示,学习简单的和较难的运算规则时,三种类型样例的学习效果不存在显著的差异;学习中等难度的运算规则时,“不完整样例—分类”的学习效果最好,完整样例的学习效果其次,不完整样例的学习效果较差。这说明,一般来说,“不完整样例—分类”的学习效果最好,但是对于较易和较难规则的学习,需要寻找另外的干预因素。
Chi等人提出了“自我解释效应”的概念,它是指为理解文字或其他媒介呈现的新信息所做出的自我理解式的解释。他们发现,在学习不完整样例时,需要对空缺的部分做出解释,将其变完整,因此,自我解释发挥了重要的作用。
(二)样例的渐减提示设计
渐减提示是指,先呈现完整样例(模型),再呈现缺少一个解答步骤的样例(带有支架的问题解决),然后呈现有越来越多空白的样例,直到只剩下需要解决的问题(独立的问题解决)。通过这种方式,实现从模型到带有支架的问题解决,再到独立的问题解决的转变。
邢强等人对此做了实验研究。他们把被试分为两组,一组叫联结学习样例组,另一组叫渐减提示样例组。每一组学习的样例都是具有不同的表面内容、相同的内在结构的四个概率问题。在联结学习样例组,样例的呈现方式是,先呈现一个样例,再把四个样例中的一个作为问题呈现(没有解题步骤),然后把这个问题的解题步骤完整呈现,以此类推,直到所有样例全部呈现。在渐减提示样例组,每一个样例的呈现方式都是,先呈现解题步骤完整的样例,再呈现解题步骤缺少最后一步的样例,以此类推,直到呈现没有解题步骤的样例。结果显示,渐减提示设计对近、远迁移都有较大的促进作用,并缩短了被试解决问题的时间,同时促进了被试对样例问题的自我解释。
(三)样例的解释法设计
解释法是指,在学习新的运算规则或符号时,将其转化为已经学过的运算规则或符号来加以解释。例如,a2可以用a×a来表示,ab可以用a×b来表示,以帮助学生理解a2、ab的运算含义。此外,“解释—标记”法是指,把运算样例中含有新运算规则或符号的运算步骤用红色字体“标记”出来。
张奇等人对此进行了系列研究,发现了许多有意义的结果:(1)用解释法样例学习分数加、减运算规则,其近迁移成绩明显优于普通样例,而远迁移成绩无显著差异;(2)用“解释—标记”法样例学习分数乘、除运算规则,其远迁移成绩明显优于解释法样例和普通样例,而近迁移成绩无显著差异;(3)用解释法样例学习比例运算规则,其远、近迁移成绩均明显优于普通样例。这些结论说明用解释法和“解释—标记”法样例学习,对迁移的产生有积极的作用。
杜雪娇等人以小学六年级学生为被试,以“完全平方和”和“平方差”代数运算样例为学习材料,进行实验研究。结果显示,采用解释法设计“完全平方和”和“平方差”代数运算样例,明显提高了代数运算規则的学习效果。进一步,他们又将样例呈现方式分为分步呈现和整体呈现两种类型:分步呈现是指,每次只呈现样例的一个运算步骤及其转换标记,待被试学习理解后,再呈现下一个运算步骤,直到学完整个样例;整体呈现是指,一次性呈现样例的所有运算步骤、运算标记和运算结果。研究发现,对于运算步骤较多的样例,采用被试自主控制的分步呈现方式的学习效果显著优于整体呈现方式。
(四)样例的步骤编码设计
Catrambone等人提出了样例学习的子目标模型,强调了样例学习中子目标的作用。他们认为,在呈现样例的解题步骤时,应通过附着标签或运用视觉分离的方法,着重强调样例的子目标,把一系列步骤组织在一起,因为这样可以促使学习者积极地归纳样例的基本目标结构,解释这些步骤为什么组织在一起,从而帮助学习者形成有用的概化,提高解决新问题的能力。也就是说,清晰地表示出子目标、达到子目标所需的策略和方法以及子目标之间的等级关系,能够改变学习者的问题表征,从而有利于学习者学习的迁移。
邵光华在三角函数综合应用的样例学习研究中,对样例问题采用分步求解的思想,分别求出三个量,实际上就是设立了三个子目标。结果表明,学习这种样例的被试错误率较低,而学习综合方程解法样例的被试错误率高。
邢强等人对样例的子目标编码在新问题解决中对原理运用的作用进行了研究。结果显示,用子目标编码样例的解题步骤有利于消除新问题解决中由于表面概貌和表面对应变化带来的消极影响,同时能够促进被试理解原理和获得原理的概化图式。
张奇等人对小学生用样例学习四则混合运算规则进行了实验研究。他们设计了有标记和无标记两种样例:有标记样例用红色虚线箭头标示出计算步骤,而无标记样例在计算步骤中没有任何标示——除此之外,二者完全相同。结果表明,运算步骤标记对学习“无括号”运算规则的促进作用明显。
(五)多重样例的呈现方式设计
邢强等人的研究表明,“变异性样例+诱发自我解释”的迁移效果最好。其中,变异性样例是指,表面内容不同、内在结构不同(解题原理相同,但解题步骤不同)的样例;诱发自我解释是指,在学习样例的过程中,对解题步骤所使用的原理进行提问,以唤起学习者对该解题步骤做进一步的自我解释。
此外,数学教学经常采用“样例(源题)+练习(靶题)”的形式。因此,样例与练习如何搭配才能取得更好的教学效果,是一个值得关注的问题。Trafton等人对这一问题做了研究。他们设计了样例和练习的两种呈现方式:交互式、分块式。交互式呈现方式是指,讲一个样例、做一个练习,再讲一个样例、做一个练习,如此循环;分块式呈现方式是指,先集中讲一组样例,再集中做一组练习。结果表明:在交互式条件下,被试比在分块式条件下解题时间短,正确迁移的数量多。
二、对小学数学教学的启示
从上述研究可以看出,样例的组织形式与呈现形式,都会对迁移的效果产生影响。据此,为了提高样例学习的效果,在小学数学教学中,可以采用如下策略:
(一)提供搭建完整样例的“脚手架”
不完整样例是删除了部分解题步骤的样例。删除样例中解题步骤的方法主要有“部分删除法”和“渐减步骤法”。部分删除法是删除所有样例中相同的一个或多个解题步骤。渐减步骤法可分为“正向渐减步骤法”与“逆向渐减步骤法”。正向渐减步骤法是指,首先呈现一个完整的样例,然后呈现删除了第一个步骤的第二个样例,接着呈现删除了前两个步骤的第三个样例……最后呈现没有解题步骤的问题。逆向渐减步骤法则是指,首先呈现一个完整的样例,然后呈现删除了最后一个步骤的第二个样例,接着呈现删除了最后两个步骤的第三个样例……最后呈现没有解题步骤的问题。在教学中,教师可以尝试利用这些方法设计不完整样例,给学生提供搭建完整样例的“脚手架”。
例1学校篮球队组织投篮练习。王老师对三名队员的投篮情况进行了统计分析(见表1)。这次投篮练习中,谁投中的比率高一些?
姓名投篮次数投中次数投中的比率李明25161625张一华20131320朱立新30181830解:为了便于统计和比较,通常把这些分数用分母是100的分数来表示。
于是,有李明投中次数占投篮次数的1625,就是64100;
张一华……
朱立新投中次数占投篮次数的1830,就是……
因为……
所以……投中的比率高一些。
其中的省略号就是解题步骤缺少的部分,需要学生补齐信息。
(二)设置样例的解释提示语和子目标提示语
解释提示语是指,对新知识从旧知识的层面给予解释,或对算法从算理层面进行解读。
数学运算规则之间普遍存在着逻辑关系。例如,乘法的意义可以用乘法分配律来解释:从乘法意义的角度看,有5×3=5+5+5;从乘法分配律的角度看,有5×3=5×(1+1+1)=5×1+5×1+5×1=5+5+5。通过这种运算样例的学习,学生能自主领悟并概括出乘法运算的规则。
支撑算法的基础是算理,使用算法只是一种工具性理解,明白算理才能达到关系性理解。例如,48×2=96可以用竖式来计算,而支撑这种算法的算理是乘法分配律:48×2=(40+8)×2=40×2+8×2=80+16=96。再如,同分母分数相加的算法是分母不变、分子相加(如27+37=57),其算理也是乘法分配律[如27+37=17×(2+3)=57]。
子目标提示语是指,把一个问题的解决分解为几个步骤,把每个步骤看成是一个子目标,对一些关键的步骤给出一些提示语,在一定量的训练后再逐步取消提示语。
例2(1)王叔叔割完一块草地需要8小时,他儿子帮他割了14,问:王叔叔还要割几小时?
(2)小红3小时粉刷一座房子,小明要用5小时,两人合刷要用几小时?
这两道题有着相同的子目標结构:先求工作量(总工作量或单位时间工作量),再求工作时间。因此,可以设置如下提示语:
①如何求工作量(总工作量或单位时间工作量)?[(1)1-14=34。(2)13+15=815。]
②如何求工作时间?[(1)34÷18=6(小时)。(2)1÷815=1.875(小时)。]
例3一辆车从甲地开往乙地,如果把车速降低10%,那么要比原定时间迟1小时到达;如果以原定速度行驶180千米,再把车速提高20%,那么可比原定时间早1小时到达。甲、乙两地之间的距离是多少?
根据题意,这道题的子目标结构如下:先求原定时间,再求以原定速度行驶180千米所需的时间,接着求原定速度,最后求甲、乙两地之间的距离。因此,可以设置如下提示语:
①原定时间是多少?[1÷10%×(1-10%)=9(小时)。]
②以原定速度行驶180千米所需的时间是多少?(1÷20%×[(9-1)×(1+20%)-9×1]=3(小时)。)
③原定速度是多少?[180÷3=60(千米/小时)。]
④甲乙两地之间的距离是多少?[60×9=540(千米)。]
(三)组织样例的同型题和远迁移题
学习迁移经典理论“相同要素说”认为:如果后面学习的材料与先前学习的材料有相同要素,那么,先前学习的材料就会对后面学习的材料产生迁移影响;两种学习材料之间包含的共同要素越多,就越容易迁移。
两个问题之间可能存在四种关系:表面概貌相同,内在结构相同;表面概貌相同,内在结构不同;表面概貌不同,内在结构相同;表面概貌不同,内在结构不同。这里,表面概貌是指问题的外貌、形式、情节等,内在结构是指问题的数量关系或解决问题的规则;相同包括相同或相似,否则称为不同。
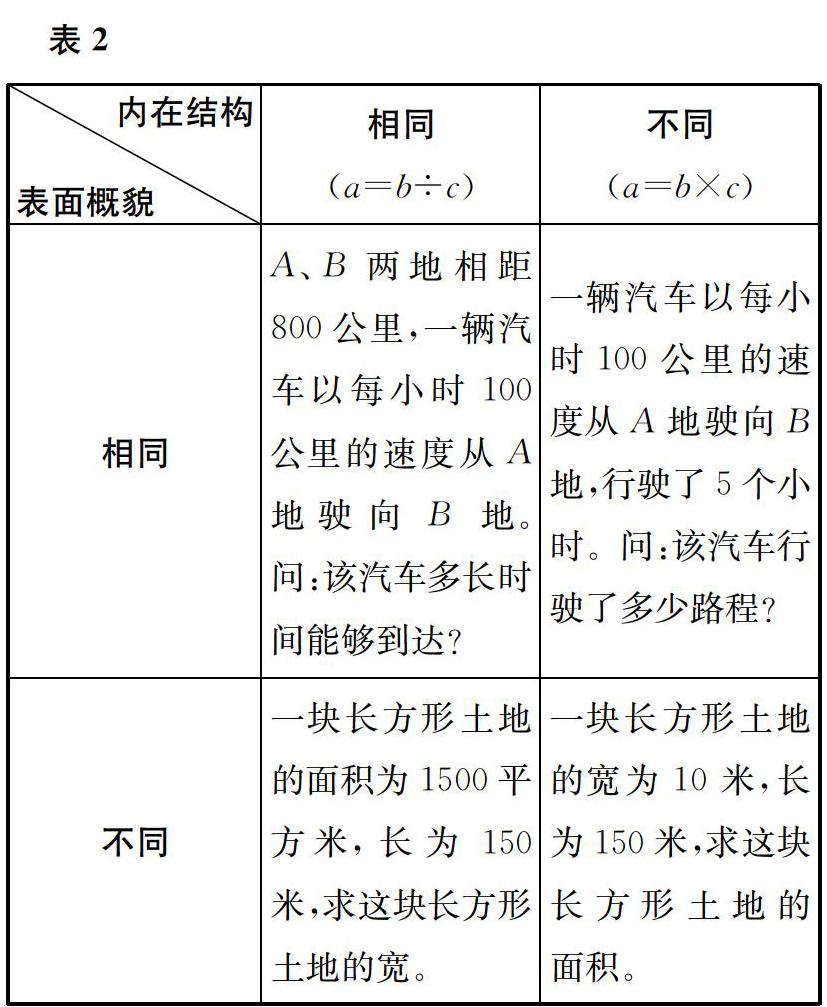
与一道题目表面概貌相同、内在结构相同,表面概貌相同、内在结构不同或表面概貌不同、内在结构相同的题目叫作这道题目的同型题。而与一道题目表面概貌不同、内在结构不同的题目叫作这道题目的远迁移题。将一道题目作为样例(源题),然后设计它的同型题与远迁移题,这样的训练方式可以有效提高学生的迁移能力。
例4A、B两地相距600公里,一列动车以平均每小时300公里的速度从A地驶向B地。问:该动车从A地到B地需要多少时间?
该题的同型题和远迁移题见表2。
(a=b×c)相同A、B两地相距800公里,一辆汽车以每小时100公里的速度从A地驶向B地。问:该汽车多长时间能够到达?一辆汽车以每小时100公里的速度从A地驶向B地,行驶了5个小时。问:该汽车行驶了多少路程?不同一块长方形土地的面积为1500平方米,长为150米,求这块长方形土地的宽。一块长方形土地的宽为10米,长为150米,求这块长方形土地的面积。例5(1)有一条长800米的公路,在公路的一侧每隔20米栽一棵树苗,需要多少棵树苗?
(2)一根彩带长6米,小红用剪刀将彩带剪成相同的长度,一共剪了5次,则得到的彩带每一段长多少?
(3)小军家在六楼,每爬一层楼需要30秒,问:小军从一楼到家需要多少时间?
这三道题目是表面概貌不同、内在结构相同的同型题。
例6(1)今年的产量比去年多110,则今年的产量相当于去年的几分之几?
(2)水结成冰之后体积增加了110,则冰融成水之后体积会减少几分之几?
(3)一件毛衣,先提价110,然后又降价110,则现价是原价的几分之几?
后两道题目是第一道题目的表面概貌不同、内在结构不同的远迁移题。
(四)将样例与练习交互呈现
教师在组织样例和练习时,可以采用交互式呈现方式。特别是对一些运算知识的学习,更宜采用这种呈现方式,因为这类知识需要及时练习、及时反馈,才能习得技能。
例如,“求长方形的周长”样例和练习的组织——
例题1篮球场长26米,宽14米,求其周长。
算法(1)26+14+26+14=80(米);(2)26+26+14+14=80(米);(3)26×2+14×2=52+28=80(米);(4)26+14=40(米),40×2=80(米)。
练习1(1)长方形毛巾的长是60厘米,宽是30厘米,它的周长是多少?
(2)计算图1中图形的边长。
例题2正方形手帕的边长是26厘米,它的周长是多少?
规律长方形的周长等于长的2倍加宽的2倍,或者等于长加宽的和的2倍;正方形的周长等于边长的4倍。
练习2(1)用4个边长为1厘米的小正方形拼成一个大正方形,这个大正方形的边长是多少厘米?它的周长呢?
(2)用6个边长为1厘米的小正方形拼成一个长方形,这个长方形的长和宽各是多少厘米?它的周长呢?
……参考文献:
[1] Stark,R.Learning by workedout examples:The impact of incomplete solution steps on example elaboration, motivation, and learning outcomes[M].Bern,CH:Huber,1999.
[2] 林洪新,张奇.小学生代数运算规则的样例学习[J].心理学报,2007(2).
[3] 张奇,郭菲菲.小学生“去括号”运算规则的样例学习[J].心理科学,2008(1).
[4] Chi,M.T.,Bassok,M.Learning from examples via selfexplanation[C]//Resnick,L.B.ed.Knowing, learning, and instruction:Essays in honor of Robert Glaser.Hillsdale,NJ:Erlbaum,1989.
[5] Renkl,A.,Atkinson,R.K.,Maier,U.H., et al.From example study to problem solving:Smooth transitions help learning[J].The Journal of Experimental Education,2002(4).
[6] 邢强,莫雷.渐减提示法呈现样例对学习迁移的作用[J].心理与行为研究,2003(4).
[7] 張奇,郑伟,万莹.“解释法”样例对小学生学习新运算规则的促进[J].心理发展与教育,2014(2).
[8] 杜雪娇,张奇.样例设计及呈现方式对学习代数运算规则的促进[J].心理学报,2016(11).
[9] Catrambone,R.Subgoal learning and the effect of conceptual computational equations on transfer[C]//Proceeding of the 22nd Annual Conference of the Cognitive Science Society.Hillsdale,NJ:Erlbaum,2000.
[10] 邵光华.数学样例学习的理论与实证研究[D].上海:华东师范大学,2002.
[11] 邢强,莫雷.样例的子目标编码对新问题解决中原理运用的作用研究[J].心理发展与教育,2003(4).
[12] 张奇,林洪新.四则混合运算规则的样例学习[J].心理学报,2005(6).
[13] 邢强,莫雷.多重样例的变异性和编码对迁移影响的实验研究[J].心理科学,2005(6).
[14]Trafton,J.G.,Reiser,B.J.The contributions of studying examples and solving problems to skill acquisition[C]//Polson,M.ed.Proceedings of the Fifteenth Annual Conference of the Cognitive Science Society.Hillsdale,NJ:Erlbaum,1993.
