以“图形与几何”为媒在深度学习下发展高阶思维

陈惠娟

【摘 要】应时代高端人才的需求，数学教育的任务在于培养学生的高阶思维，高阶思维的课堂教学的目标指向培养学生的分析、综合、提问、批判、创造等发生在较高认知水平层次上的能力。在深度学习的背景下，以“图形与几何”为例，从举一反三、整理自学、反省错误方面去培养学生提出和解决问题的能力、分析和综合信息的能力，批判和创造事物的能力，有意识地去培养学生的高阶思维。

【关键词】高阶思维;深度学习;图形与几何

一、始于理解—高阶思维的涵义

杜威认为高阶思维即是反省思维。美国教育家布卢姆将思维过程具体化为六个方面，包括记忆、理解、应用、分析、综合、评价。前三项通常被称为低阶思维，后三项通常被称为高阶思维，而且常常被等同于批判性思维。也有学者将批判性思维仅仅看成是第6个层级即评价，因为正是这个层级“聚焦于在对一个陈述或命题的分析的基础上做出评价或判断”。由此看来，批判性思维只是高阶思维的一部分。之后，高阶思维又被修订为分析、评价和创造。

高阶思维的概念在不断地变化发展中，但不管怎么变，高阶思维的课堂教学的目标都指向于培养学生的分析、综合、提问、批判、創造等发生在较高认知水平层次上的能力。其中，“提问”就是提出问题的能力，它常常和解决问题的能力放在一起论述，但爱因斯坦曾说：“提出一个问题往往比解决一个问题更重要。”所以这里只把“提问”放在“高阶思维”能力的内涵里。还有学者提到“决策能力”也属于高阶思维能力，而这里没有把“决策”放在里面，是因为这种能力属于“元认知”范畴，在本文中就暂不作研究了。

为什么说在深度学习背景下发展高阶思维呢？因为小学数学深度学习是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与，体验成功，获得发展的有意义的数学学习过程。在这个过程中，学生开展思维活动，获得数学核心知识，把握数学的本质和思想方法，提高思维能力，发展核心素养，形成积极的情感、态度和价值观，逐渐成为具有独立性、批判性、创造性又有合作精神的学习者。可以看到，深度学习旨在发展学生的高阶思维和关键能力。因此，发展高级思维的过程就是深度学习的过程。

二、归于实践—高阶思维的培养

高阶思维的培养也不能说没有在小学发生过，其实，这样的培养活动一直在进行着，只不过显得那么“润物细无声”。在深度学习的背景下，数学教育越来越重视发展学生的思维尤其是高阶思维的培养。这样的培养目标放在了一个较高的位置，而且是“大张旗鼓”地进行着，以下是从“图形与几何”领域方面展开的研究：

（一）举一隅知三隅，发展孩子提出和解决问题的能力

孔子曰：“举一隅不以三隅反，则不复也。”教师不能总是让孩子做“地毯式”练习，在深度学习的课堂上，教师要学会给孩子减负，有意识地并坚持地对问题进行变式训练，笔者相信孩子会超越其“最近发展区”而达到下一发展阶段的水平。例如：

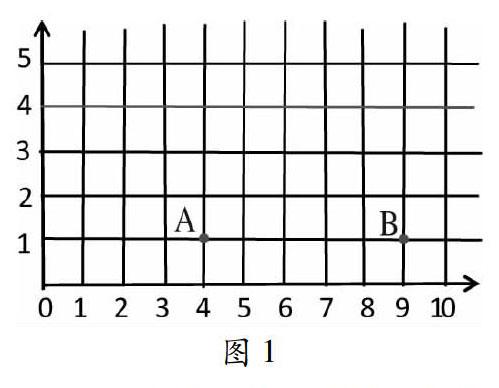
如图1，三角形ABC，点A（4，1），点B（9，1），如果点C（X，4），那么：

（1）当X=？时，三角形ABC是直角三角形。（2）当X=？时，三角形ABC是等腰三角形。在这样的问题情境中，教师一点拨：“只能形成这样特殊的三角形吗？”学生一定会受到启发，不自觉地想要提出问题：（3）当X=？时，三角形ABC是锐角三角形。（4）当X=？时，三角形ABC是钝角三角形。（5）当X=？时，三角形ABC是三边不等三角形。

学生能够提出这些问题的前提是问题情境要有一定的空间，如果太狭隘，也很难达到这样的效果。在这样的前提下，学生通过举一反三，把这类问题可能提到的各种三角形都囊括在里面了，如果只是单纯地解决“直角三角形”和“等腰三角形”这样特殊的三角形问题，学生的思维永远只能停留在“点”的静止状态，但有了不特殊三角形的自问后，他们的思维就被彻底打开了，原来这里的点在运动着，最后连成了一条Y=4的直线。在以后思考这类问题的时候，学生会以动态的眼光来看这样一个静止的事物，这样的思维在以后的学习中非常重要。

各种各样的问题层出不穷，但只要学会举一反三，就能将同类问题一网打尽，这是一种多么高效的学习方式！所以，教师在课堂教学中一定要经常举一反三，进行变式训练，继而学生自己能够就某个问题进行举一反三，自己提问，自己解决，学生的高阶思维由此得到发展。

（二）整合知识并自学，提高孩子分析和综合信息的能力

数学知识有自身的结构和系统，而孩子的认知结构有可能是零散的，被割裂的，这样不利于解决综合信息强的问题，而在这样一个信息化时代，学生将来面对的问题必将是综合性的、系统性的、复杂性的。学生脑中不仅要有系统的知识结构，还要学会自己阅读、分析信息的能力。

例如：有以下4种规格的长方形、正方形玻璃：①长0.6米，宽0.4米;②长0.6米，宽0.5米;③长0.5米，宽0.4米;④边长0.4米。选5块，拼成无盖长方体（或正方体）鱼缸。问题1：可以选几种规格的玻璃，各要选几块？你能想到多少种不同的选法？问题2：做鱼缸，推荐做哪种？这就是一个综合性问题，孩子在解决这样一个问题时，必然要分析这两个子问题的本质是什么，问题1指的是表面积，问题2指的是体积，而前提是头脑中要有一个长方体和正方体的表面积和体积的系统知识，也就是思维导图，为何叫“导图”？因为它会引导我们理清表面积中各个棱长或者面积之间的关系，解决这个问题时就更加得心应手。

因此，教师应该帮助学生学会整理知识，在课堂上或练习中给出一段材料让孩子自学，放手让孩子自己去阅读、去分析、去综合，从而提高学生的分析和综合信息的能力，在这个过程中，高阶思维得到提升。

（三）反省自误生真理，培养孩子批判和创造事物的能力

为什么这里一定是反省错误呢？因为“错误本身是达到真理的一个必然环节，由于错误，真理才会发现。”德国哲学家黑格尔说道。在深度学习的课堂上，教师要让学生对自己的作品有一个反思、评价的过程，而教师更应该用批判性的眼光去看待每一个学生在课堂上的生成。

例如，平行四边形面积的探索过程：它的思想就是把这个平行四边形转化成长方形，从而建立联系推导出公式，怎么转化呢？学生对这个问题展开研究，这个过程孩子们在创造，但思维层次不同。层次一：减拼三角形;层次二：减拼梯形;层次三：

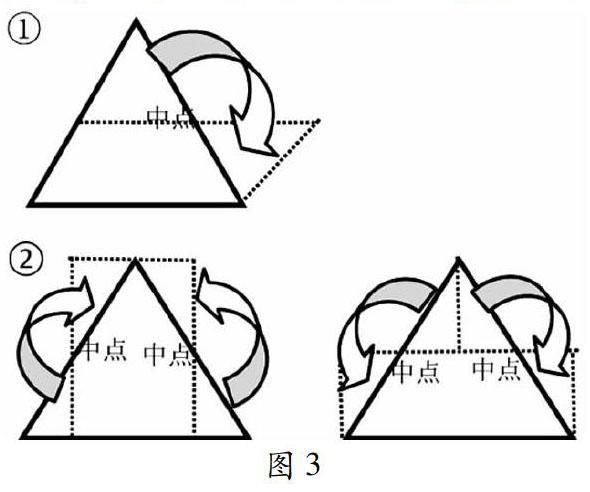
面对左边这样两份资源，有可能教师自己都没有多想：“为什么这样剪下两个三角形不能成功呢？”直接忽略掉了这样的一种可能性，而有批判性眼光的教师则会更进一步地带着孩子一起想一想：“这样随便从斜边出发不行，怎样就行呢？”这样一启发，学生豁然开朗，直觉地发现：只要从斜边的中点剪就可以。接着通过实际操作和验证得到从中点剪下两个直角三角形，通过平移和旋转能转化成长方形。这样的过程同样适用于三角形面积和梯形面积的探索：①把三角形转化为平行四边形（面积不变）;②把三角形转化为长方形（面积不变）。〖XC48-3.TIF〗〖TS（1〗图3〖TS）〗

对于课堂上的生成资源，教师首先要有批判性的眼光，常常和学生交流这样一句话：“这样可以吗？为什么可以/不可以？”有时候教师的思考会跟不上学生的思考，也许教师还不能解决这个问题，但学生会给你意想不到的惊喜，学生通过讨论交流，会“帮助”教师把问题解决了！因此，重要的是教师要给学生这样的机会去思考，长此以往，学生也会带着批判性的眼光去看待和思考问题。正因为有批判，才会有创造，进而培养孩子的高阶思维。

参考文献：

[1]郭小山.核心素养背景下小学数学思维能力的培养——以“图形与几何”为例[J].华夏教师，2018（35）.

[2]李娟.浅谈小学数学核心素养下的空间观念培养——以《图形与几何》为例[J].名师在线，2019（01）.

[3]马军荣.浅谈小学“图形与几何”教学中的“核心素养”教学——人教版小学数学核心素养观摩交流会听后心得[J].数学学习与研究，2018（04）.