基于MCMC方法的顾客满意度的Bayes估计

赵琪

摘要：该文提出运用MCMC方法，解决顾客满意度的Bayes模型中的数值计算问题。简要介绍了MCMC方法。运用顾客满意度的Bayes模型进行了实例分析，并且运用OpenBUGS软件给出了在先验分布为Dirichlet分布情况下的Bayes模型的数据仿真。

关键词：顾客满意度;Bayes模型;MCMC方法;OpenBUGS软件

中图分类号：0212.8 文献标识码：A

文章编号：1009-3044（2020）14-0133-02

自20世纪70年代，顾客满意度（Customer Satisfaction）的研究在欧美等西方国家开始兴起。20世纪末，我国也开始进行国家满意度指数模型的设计工作。目前，对顾客满意度进行测量和研究已成为企业的一项重要工作内容，顾客满意度是衡量企业整体质量的重要指标，另外它还广泛应用与国家、行业等宏观、中观分析。已有许多高校和市场研究公司参与到顾客满意度模型的研究中来。其中，苗敬毅提出了顾客满意度的Bayes模型。本文运用马氏链蒙特卡洛方法（MCMC），解决顾客满意度的Bayes模型中的数值计算问题。

1顾客满意度的Bayes模型

1.1 Bayes统计的基本思想

贝叶斯统计学是统计学的重要流派，具有广泛的应用与影响力，它与经典统计学的主要区别是使用先验信息（经验或历史资料）。假设θ是我们感兴趣的一个未知量（θ所有可能值的集合称为参数空间，记为@），按贝叶斯的观点，我们将它看做随机变量，可以用一个概率分布去描述它，这个分布称为先验分布嘲。贝叶斯公式结合了θ的先验信息和样本信息（x）得到了样本给定下θ的条件分布称为θ的后验分布，记为π（θx），一切决策和推断都是基于后验分布做出，下面给出后验分布的确定方法。

后验分布是在样本信息给定的前提下集中了样本信息与先验分布中有关θ的一切信息，因此后验分布π（θx）要比先验分布π（θ）更贴近实际情况，具有更高的可信度。作为θ的估计一般采用后验分布π（θk）的某个位置特征量，例如后验分布的分位数或数学期望。本文采用θ=E[πx]。

1.2顾客满意度的Bayes估计

顾客满意度的Bayes估计实际上是一种多级评分的Baycs估计。多级评分的Bayes估计文献[3]中已有详细的证明，在这里我们引用其主要结论。假设在某种指标体系下，每个指标的可能测评分数为0，1...K。假设指标体系由n个指标构成，测评分数为0分的指标有xo个，……，评K分的有xg个。对每一测评

MCMC运算的软件和应用程序已经有很多被开发出来，例如OpenBUGS软件，对于许多常用的模型和分布进行Gibbs抽样时使用OpenBUGS都是非常方便的。因为在使用Open-BUGS时，只要设置好变量的先验分布并对所研究的数学模型进行一般性的描述，就可以很容易实现对模型的贝叶斯分析，不需要知道参数的先驗密度或似然函数的精确表达式，也不需要复杂的编程。

3数据仿真

我们以文献[1]中的实例为例，说明MCMC方法的运用过程。

此例为一企业人力资源关于公司员工满意度调查。指标体系采用国际通用型量表，涉及指标33项，样本数据79例。评分规则是：1-肯定是;2-偶尔是;3-不确定;4-偶尔不是;5-肯定不是。调查统计数据表格见文献，在此不再赘述。

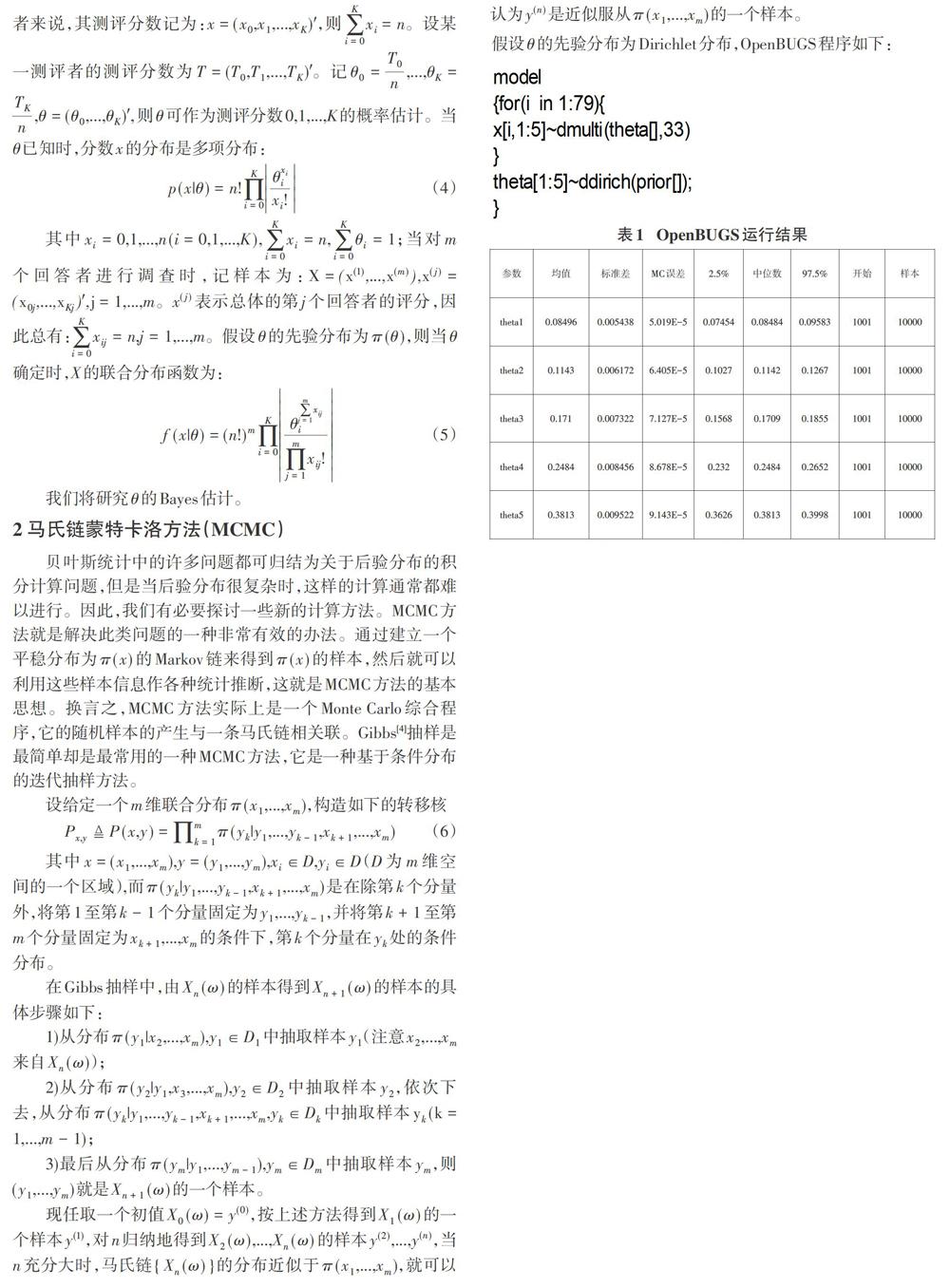
我们在模型运行的过程中，为确保参数的收敛性，首先进行1000次预迭代。然后丢弃最初的预迭代数据，再进行10000次迭代。下面是得到的参数θ的部分信息。

在表中可以看出，员工的满意度θ的Bayes估计为：θ=（θ1……θ5）'=（0.08496，0.1143，0.171，0.2484，0.3813），θ是评分为1……5分的概率的估计，即员工对公司总体持非常满意态度的约占38%，持比较满意态度约占25%，没有特殊意见的约占17%，持不满意态度的约占11%，持非常不满意态度的约占9%。与文献[1]的结果一致。除了得到参数的均值以外，从表中还可以得到参数的、95%置信区间、后验分布的标准差和中位数等信息。从OpenBUGS软件还可以得到参数的后验分布的核密度估计、动态轨迹图、迭代历史和收敛性统计诊断图等一系列信息。另外，除了直接编写代码程序以外，在Open-BUGS中还可以使用有向图模型方式（Doodle模型）。在此不一一赘述。

4结束语

MCMC方法的诞生使贝叶斯统计学如虎添翼，获得突飞猛进的发展，长期以来被认为是难以处理的模型，如今借助MC—MC方法已经可以定量研究。这种方法的应用戏剧性地重塑了统计学家的工作方式，构建了以随机模拟技术为手段的统计研究模式。我们把McMC方法运用于顾客满意度模型，显示了此方法的广泛应用性。本文的研究为这种方法应用于更多的贝叶斯模型提供了启示。