机器学习方法在中医证候分析中的应用

张龙 王国明

摘要：传统的中医辨证诊疗主要基于“望、闻、问、切”得到的四诊信息，由于掺杂过多的医师主观因素，即使对同一个病人的辨证结果也可能不尽相同，因此如何建立一个科学而规范化的中医证候的量化标准是一个值得研究的课题。本文将机器学习中的层次聚类和因子分析方法应用于中医证候量化分析，通过对采集到的1499例典型高血压病例的处理与分析，实验结果表明，机器学习方法可以有效地挖掘中医证候中隐藏的信息，为中医辅助诊疗提供重要的途径。

关键词：机器学习;因子分析;层次聚米;数据挖掘;证候扮析

中图分类号：TP391 文献标识码：A

文章编号：1009-3044（2020）14-0001 1-03

层次聚类算法出现于1963年，其指导思想是对给定的待聚类数据集合进行层次化分解。因子分析最早出现于1904年英国统计学家斯皮尔曼（C.Spearman），最初应用于心理学与教育学中，其主要目的是对显在变量找出其潜在变量（因子），用少数的潜在变量来揭示相互之间有关系的显在变量，将具有相同本质的变量归纳为一个因子。

聚类分析在中医领域有诸多的应用，如阮雪萍等人将聚类分析应用于探究阻塞性睡眠呼吸与血清SOD、MDA的相关性研究;钟小雪等人提出基于聚类分析的中醫症候的研究。因子分析同样高频率的出现在中医的应用中，如李亮亮等人基于因子分析对中医证素辨证研究。而本文以高血压病例为例，探索基于聚类分析和因子分析在中医证候中的应用。

1层次聚类算法

1.1数据来源

本文的数据是来源于全国五所医院中提取的1499份高血压患者的四诊信息，将筛选过后符合标准的四诊信息进行编码。

1.2基本思想与算法流程图

1.2.1基本思想

层次聚类法是使用比较广泛的一种方法，这种方法首先把多个变量各自看作为一个类簇，根据两个类之间的相似性统计量，把两个最接近的类簇合并成一个新的类簇，计算新的类簇和其他各类簇间的相似性统计量，再选择最接近的两个类簇合并成一个新的类簇，直到达到设定的分类数目为止。相似性统计量通常是以距离为相似性统计指标常用的指标有欧式距离、重心法、最长距离法、离差平方和法（Ward法）。本文是基于离差平方和法进行两个类簇之间距离的计算，其主要是基于方差分析的思想，如果分类正确那么同类簇的样品之间的离差平方和较小，类簇与类簇之间的离差平方和较大。

1.2.2算法流程图

1.3实验结果

实验是将筛选过后的四诊信息变量进行聚类。使用R语言的hclustf）函数或者SPSS软件都可以画出聚类图。聚类结果如下图2所示。

1.4层次聚类实验结论

由于聚类分析是无监督学习，在分类过程中，它能自动的将样本进行归类处理，减少了主观判断造成的分析误差，使得分类的结果更加具有客观性和科学性。但同时我们也意识到对于中医这种专业性比较强的领域，在部分聚类分析的结果中，可能会出现没有临床症状的四诊信息会被聚为一类，也有可能出现并无关联甚至相互矛盾的症状被聚为一类。而因子分析作为一类降维的相关分析技术，其主要目的是从多个变量中找出因子，以少数几个因子解释一群具有相互关系的变量，因其能够根据权重反映变量自身的重要程度，提高综合评价的效率，近些年来被广泛应用于社会学、管理学、经济学等领域中。

2因子分析

2.1基本思想

探索性因子分析（Exploratory Factor Analysis，EFA）可在许多变量中找出隐藏的具有代表性的因子，将相同本质的变量归入一个因子，从而减少变量的数目，还可检验变量间关系的假设。通常探索性因子分析是以协方差为基础来估计其方程的参数，这就要求数据是连续的并且服从正态分布。但是中医中收集到的四诊信息通常是等级资料，无法满足因子分析的潜在变量和显在变量均为连续变量的前提条件。因此利用基于协方差系数矩阵的因子分析方法对收集到的四诊信息进行分析，可能会出现错误的结果。Muthen后来提出了将等级资料变换为潜在连续变量，求得连续变量间多项相关系数，以多项相关系数进行探索性因子分析。本文采用基于多项相关系数矩阵的探索性因子分析和基于协方差矩阵下的探索性因子分析进行比较研究。

2.2数据建模

2.2.1协方差系数矩阵下的因子分析建模

2.3.1因子可行性分析

在对数据进行因子分析时，需要检验数据间是否存在一定的相关性，如果不存在相关性，则对该数据进行因子分析则毫无意义。进行可行性分析常用的方法有KMO系数与Bartlett卡方检验。

从表1的检验结果来看，KMO值等于0.832，接近于1，说明所有变量之间的简单相关系数平方和远大于偏相关系数平方和，因此适合于作因子分析;此外，从Bartlett球形检验的结果也可以发现，其相伴概率几乎等于零，远小于显著性水平，则拒绝原假设，说明原始相关系数矩阵不可能是单位阵，即原变量之间存在相关性，适宜作因子分析。

2.3.2确定公因子个数

通常情况下，探索性因子分析中所提取的因子数量主要由特征根、方差累计贡献率以及碎石图等来决定。其中所提取因子的特征根一般要求大于1，且累计方差贡献率要达到80%以上才能保证因子具有较强的解释力度，但由于本文中数据的变量个数过多，因此需要结合特征根及其差值（表2）以及碎石图（图4）来选取因子。

首先从特征根及其差值（表2）来看，基于协方差矩阵的因子分析法和基于多项相关系数矩阵的因子分析法所提取的前5个因子的特征根都是大于1的，并且其差值相对较大，从第6个因子开始，特征根的差值逐渐变小，因此我们可以考虑选取5个因子。此外，从图4的两种因子分析方法下的碎石图来看，都是在第6个因子处具有一个明显的拐点，第6个因子开始趋于平滑曲线，这与特征根及其差值的结论相一致，即两种方法对于所提取的因子数目没有太大差别，都是提取5个因子较为适宜。

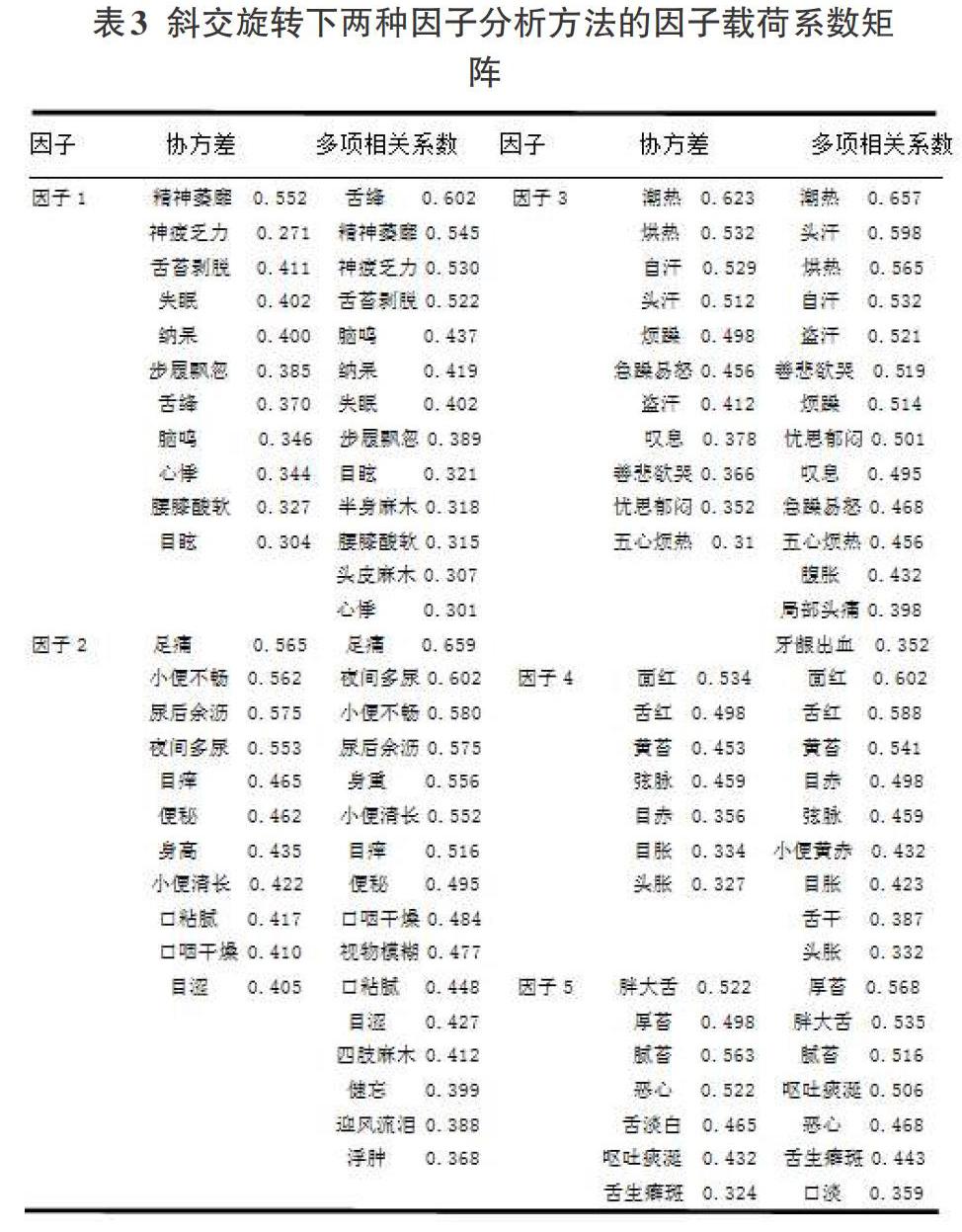
2.3.3结果（见表3）

2.4因子分析实验结论

从因子载荷系数矩阵整体来看，两种方法所提取的五个因子都存在其相对应的中医证候。从每个因子所对应的中医证候的载荷系数大小来看，基于多项相关系数矩阵的因子分析法更为精确、细化，并且载荷系数普遍高于基于协方差矩阵的因子分析方法下的载荷系数.这说明，如果取载荷系数较大时，基于协方差矩阵的因子分析方法极易忽略一部分变量，从而造成一定的分析误差。综上，使用基于多项相关系数矩阵的探索性因子分析方法所得到的结果更为合理可靠。