钢轨砂带打磨残余应力的试验与仿真研究*

王文玺， 李建勇， 吴 源， 樊文刚

(1. 重庆大学 机械工程学院， 重庆 400044)(2. 北京交通大学 机械与电子控制工程学院， 北京 100044)(3. 重庆大学， 机械传动国家重点实验室， 重庆 400044)

钢轨打磨是世界公认的最有效且最常见的轨道养护技术[1]。通过预防性和修复性打磨，可以消除轨道表面病害、修复轨道表面廓形而改善轮轨接触关系，延长钢轨使用寿命。然而，高速铁路、重载铁路、城市地铁等现代轨道交通系统的快速发展，导致了轨道养护需求的不断增加和作业时间的日益紧张，这也推动着钢轨打磨设备和技术朝着更加高效、智能和多样化方向发展[2]。

鉴于现代砂带制造技术的快速发展和高性能磨料的出现，以及考虑到现有钢轨打磨技术的应用局限性，研究人员提出了一种基于砂带磨削技术的新型钢轨打磨技术——钢轨砂带打磨(abrasive belt rail grinding, ABRG)[2-6]。ABRG充分利用了砂带弹性磨削、冷态磨削和高效磨削等优势[7]，很好地满足了钢轨打磨的要求。ABRG的基本工作原理和结构如图1所示。从图1中可知：接触轮由弹性橡胶层和刚性轮毂组成，加载力F驱使砂带与轨道表面接触，进而发生材料去除。

图1 钢轨砂带打磨基本原理

近年来，ABRG的相关研究主要集中在钢轨廓形的修复方法和砂带的服役寿命控制方面。WANG等[2]利用内凹接触轮对ABRG的静态接触行为进行了建模和研究，为钢轨轮廓的精确修复奠定了理论基础。FAN等[3]在考虑钢轨波磨影响的基础上，建立了对应的材料去除模型。此外，HE等[4]基于赫兹接触理论开展了接触压力对ABRG性能影响的试验研究并论证了其有效性。针对ABRG中的砂带磨损问题，HE等[5]着重研究了钢轨打磨过程中砂带的磨损形式和磨损过程机制。此外，CHENG等[6]则提出了一种基于声信号的砂带磨损状态监测方法。

除钢轨轮廓外，钢轨表面的残余应力也是影响钢轨使用寿命的重要因素[8-9]，尤其是对钢轨的疲劳强度和耐腐蚀性有直接影响。然而，国内外关于钢轨打磨后残余应力状态的相关研究甚少，尚未发现钢轨线上打磨后的残余应力实测数据的相关报道。由于磨削工艺参数对残余应力的影响未知，ABRG虽然能对钢轨进行修形，但也有降低其抗疲劳寿命的潜在风险。

因此，首先在自建专用试验台上测量ABRG后的残余应力状态，研究磨削工艺参数对轨面残余应力的影响规律。然后，借助三维有限元仿真方法，探究微观接触面摩擦系数、磨粒切入深度以及磨粒切削速度对钢轨表层残余应力分布的影响机制。

1 钢轨打磨试验研究

1.1 试验方案与设备

为了获取打磨工艺参数对钢轨表面残余应力的真实影响，基于自建的专用钢轨砂带打磨试验台进行试验研究。所用砂带为：VSM公司P36氧化铝陶瓷砂带，钢轨为：UT1Mn材质的GB60 kg/m 轨。接触轮、砂带和钢轨的相关参数见表1。

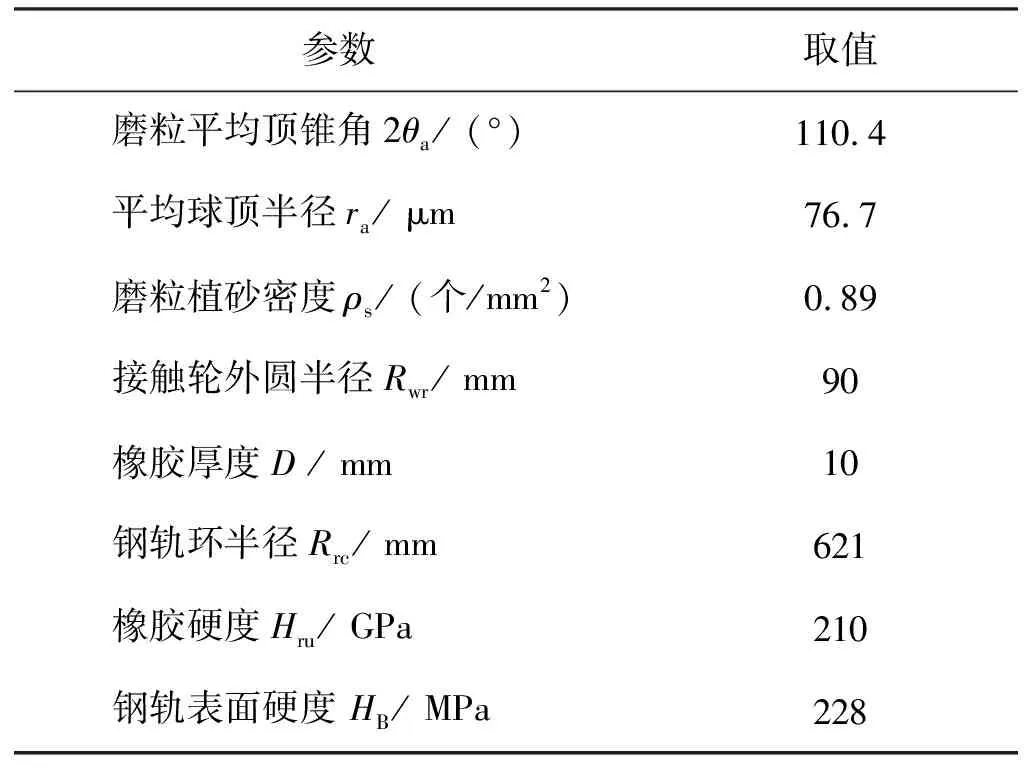
表1 接触轮、砂带和钢轨相关参数

试验选用日本PULSTEC公司的μ-X360s型便携式X射线残余应力分析仪测量残余应力[10]，如图2所示。该设备可通过圆形全二维探测器经一轮照射得到所有衍射Debye环，进而计算出2个正交方向上的残余应力。μ-X360s代替了测量过程中对精密测角仪的需求，并提供了±5 mm的定位公差，使现场测量成为可能。

图2中残余应力测量位置A、B、C、D沿钢轨环周向中心线等距分布，分别由μ-X360s测量以获得每次磨削后在X方向(轨道方向)和Y方向(径向)上的残余应力σ11和σ22。表2给出了测量所需的相关参数设置。

图2 残余应力测量方案

表2 残余应力打磨试验工艺参数

1.2 接触压力的影响

图3为表2中1#条件下磨削的X、Y方向的残余应力。在图3a中，残余应力σ11的幅值(应力大小的绝对值)随Fn的增大而增大，峰值达到311 MPa。这一趋势与周清跃等[12-13]的研究结果一致。原因可能是接触压力的升高增加了磨粒的切入深度[14-15]，同时磨削热积累也促进了残余应力值的增长[16]。图3b表明：约80%的残余应力以压应力的形式存在，并且每个Fn下的平均应力幅值与接触力呈正相关。但还是存在一些以拉应力形式存在的σ22，考虑到其幅值较小以及可能存在的测量误差，可将其假设为无应力状态。

1.3 砂带速度的影响

图4为表2中2#条件下磨削的X、Y方向的残余应力。从图4a可以看出：vb越高，σ11均值越大，vb水平方向的平均值分别为83、117、167、210和227 MPa，均呈拉应力形式。该趋势与WANG等[13,16]的研究结果具有较高的相似性。其中残余拉应力幅值随砂带线速度递增，可能是由于砂带速度的提高增加了磨削热积累所致。根据图4b可知：σ22与vb未呈现单调性变化，即使在相同工艺条件下，A～D4个部位的残余应力差距也较大，并分别以残余拉、压应力形式存在，峰值分别为159 MPa和-272 MPa，这与开式砂带磨削的试验结果明显不同[15]。对比图4a和图4b还可发现钢轨波磨对σ22的一致性影响很大。因此，在列车打磨单元设计时，须注意接触压力的精确控制以及其控制系统的动态性能调节。

(a)X方向残余应力X residual stress(b)Y方向残余应力Y residual stress图3 接触压力对表面残余应力的影响Fig. 3 Effect of contact force on surface residual stresses

(a)X方向残余应力X residual stress(b)Y方向残余应力Y residual stress图4 砂带速度对表面残余应力的影响Fig. 4 Effect of belt speed on surface residual stresses

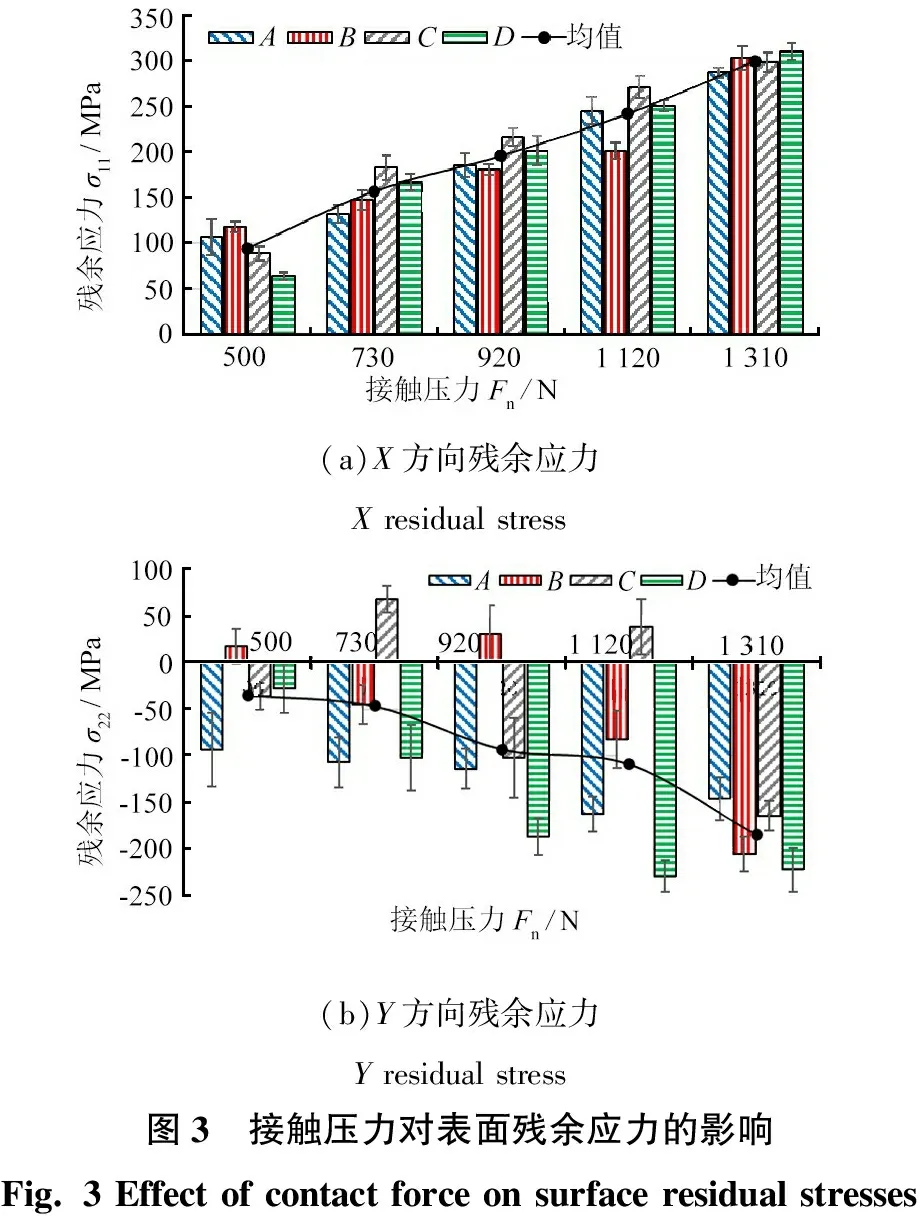
1.4 列车速度的影响

图5为表2中3#条件下磨削的X、Y方向的残余应力。图5a显示，当vf增大时σ11均值以拉应力的形式逐渐减小。这可能是由于vf的增加减少了钢轨表面通过磨削区域所需的时间，进而削减了磨削热积累和残余拉应力强度。在图5b中，除vf=5 km/h对应的残余应力为压应力外，其他试验组结果表现为差异较大的并存残余拉、压应力。

(a)X方向残余应力X residual stress(b)Y方向残余应力Y residual stress图5 列车速度对表面残余应力的影响Fig. 5 Effect of belt speed on surface residual stresses

2 单磨粒划擦有限元分析

2.1 有限元模型及仿真方案

利用ABAQUS软件建立了单磨粒划擦有限元模型。由于磨粒切削残余应力的形成过程是典型的热力耦合过程[17-19]，因此选择了热力耦合动力显式求解器。有限元模型如图6所示，磨粒外形简化为球顶圆锥。由于氧化铝陶瓷磨粒硬度通常显著高于钢轨表面硬度，故将其视为一个刚体，并对磨粒上所有节点同磨粒上表面中心参考点P施加刚性约束。磨粒单元类型选为C3D4T，网格尺寸约为4 μm，磨粒和钢轨的材料参数信息见表3。

工件尺寸为800 μm(L)×400 μm(W)×100 μm(H)；单元类型选为C3D8RT，上表层40 μm范围内单元尺寸为1 μm，其余为20 μm。钢轨的本构方程采用Johnson-Cook模型[20]，其材料参数及材料损伤参数见表4。

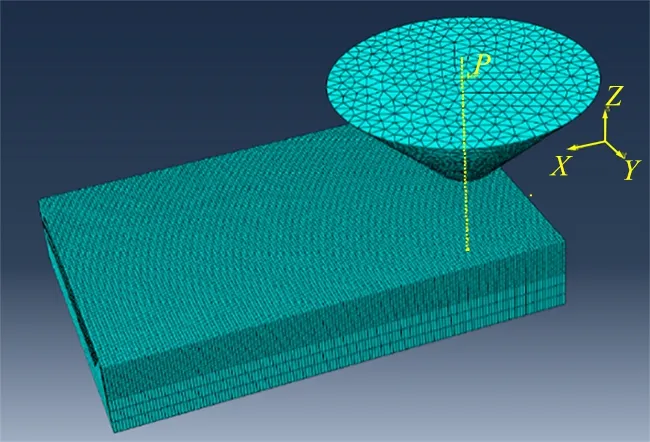
图6 单磨粒切削有限元仿真模型

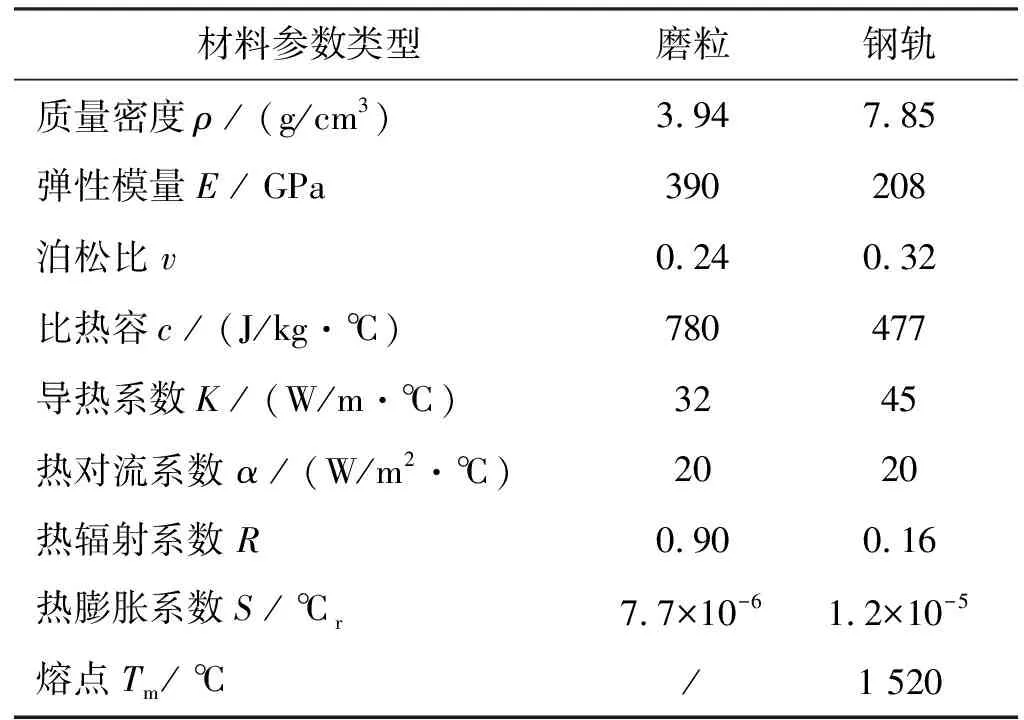
表3 磨粒、钢轨材料物理性能参数

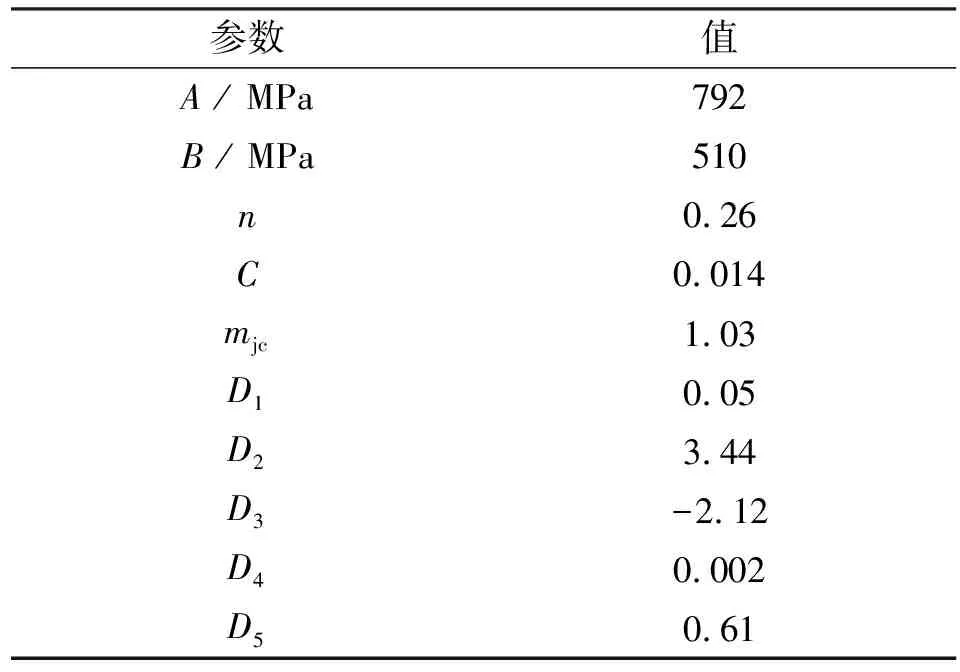
表4 钢轨材料Johnson-Cook参数

对于有限元边界条件，将工件底部设置为全自由度约束，磨粒位移载荷施加在P上，令磨粒仅能在X和Z方向上移动，如图7所示。其中，μ为接触界面的摩擦系数、r为磨粒尖端半径、δ为切入深度、v为切削速度、γ0为磨粒前角。整个模型的初始温度设定为20 ℃，磨粒表面和工件上表面设置为随环境发生热对流和热辐射。工件摩擦热流分配系数设为0.86。

5个影响因素的默认值为μ=0.20[23]，r=55 μm，δ=10 μm，v=30 m/s，γ0=-45°。磨粒在X方向以恒定速度从工件中心线开始划擦，总划擦长度为600 μm，其中切入区和切出区长度均为60 μm。如图7所示：每次模拟后，沿着划痕路径将工件对半抛开，在残余应力分布相对稳定的区域内选定5个沿X方向等距分布的点位，分别记为L1、L2、L3、L4和L5。提取L1—L5在同一深度的残余应力σ11和σ22并计算其平均值。

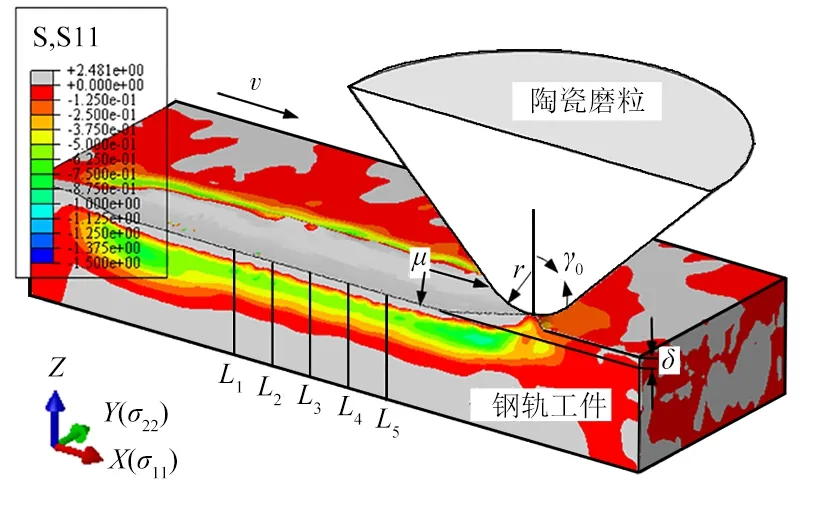
图7 仿真与测量的原理图

2.2 摩擦系数的影响

图8为不同摩擦系数下X和Y方向残余应力的变化曲线。如图8a所示，除无摩擦条件外，残余应力σ11首先在较浅位置产生拉应力，然后出现压应力，最终又回复为轻微拉应力。在较浅位置的拉应力阶段，外表面应力幅值随μ增大而增大，但增长速率逐渐减小。推测此阶段σ11的增大是由于μ的增大导致磨粒后端加工表面附近摩擦力增大，从而使加工表面间的拉应力增强。此外，μ的增大还增加了摩擦热，进而升高了表面温度，如图9所示，这促进了残余拉应力的产生及其幅值的增大。但μ的变化对最大残余压应力的幅值和位置影响不大(保持在d=19 μm，幅值约-600 MPa)。表层残余压应力的分布深度范围与μ呈正相关，说明挤压摩擦力的增大导致深层材料沿摩擦方向发生了塑性和弹性变形。上述关于σ11的结果与RECH等[15]的结果基本一致，可证明仿真有效性。

在图8b中的Y方向上，σ22的趋势与σ11的趋势相似，但它从外表面开始就呈下降趋势，这不同于σ11的先升后降。另外，在5～40 μm深度的残余应力层中，σ22在不同μ下的分布基本相同。此外，还可发现无摩擦下的磨粒划擦更有利于Y方向残余压应力层的产生。这可能是由于较小的摩擦会降低摩擦热积累的强度和范围，从而阻碍拉伸残余应力的形成[20,29-30]。

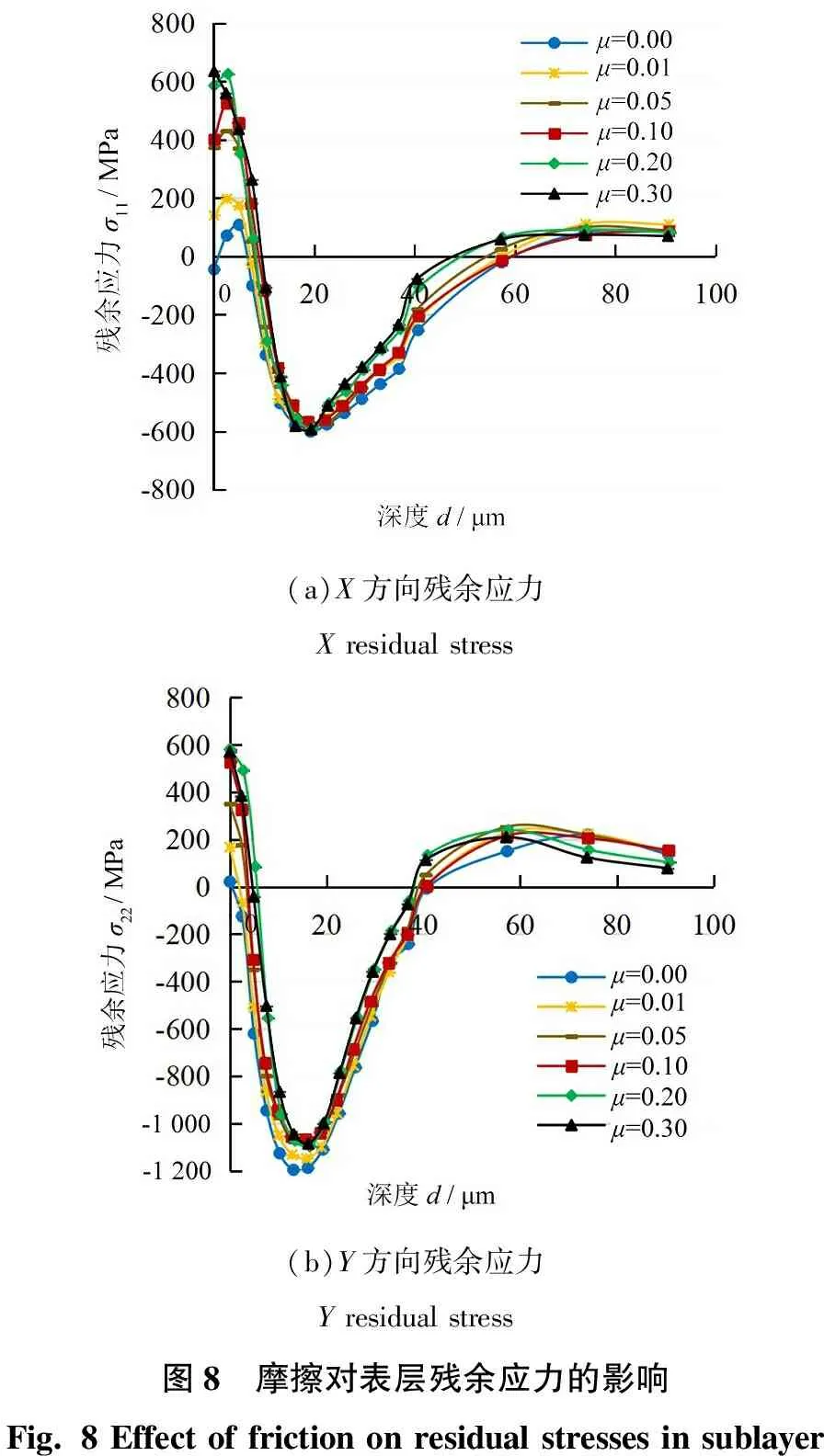
(a)X方向残余应力X residual stress(b)Y方向残余应力Y residual stress图8 摩擦对表层残余应力的影响Fig. 8 Effect of friction on residual stresses in sublayer

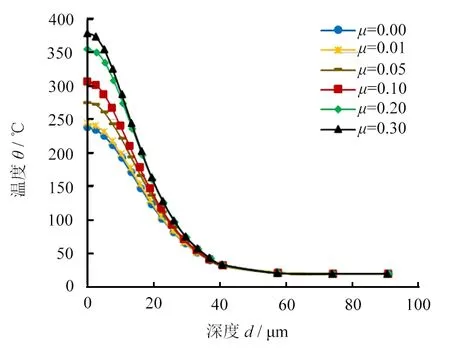
图9 不同摩擦系数对表层温度的影响

2.3 切入深度的影响

图10为磨粒切入深度对表层残余应力的影响。从图10所示的结果来看，切入深度的增加会导致更多材料体积的塑性流动和弹性变形。因此，在X和Y方向上都形成了较厚的残余压应力层，这与RECH等[15,24-25]的仿真结果相一致。在划痕表面，当δ=1 μm时，σ11和σ22的幅值均显著低于其他具有较大δ时的情况；而当δ>1 μm时，δ的变化对残余应力类型(拉应力)和幅值(约600 MPa)的改变不明显。

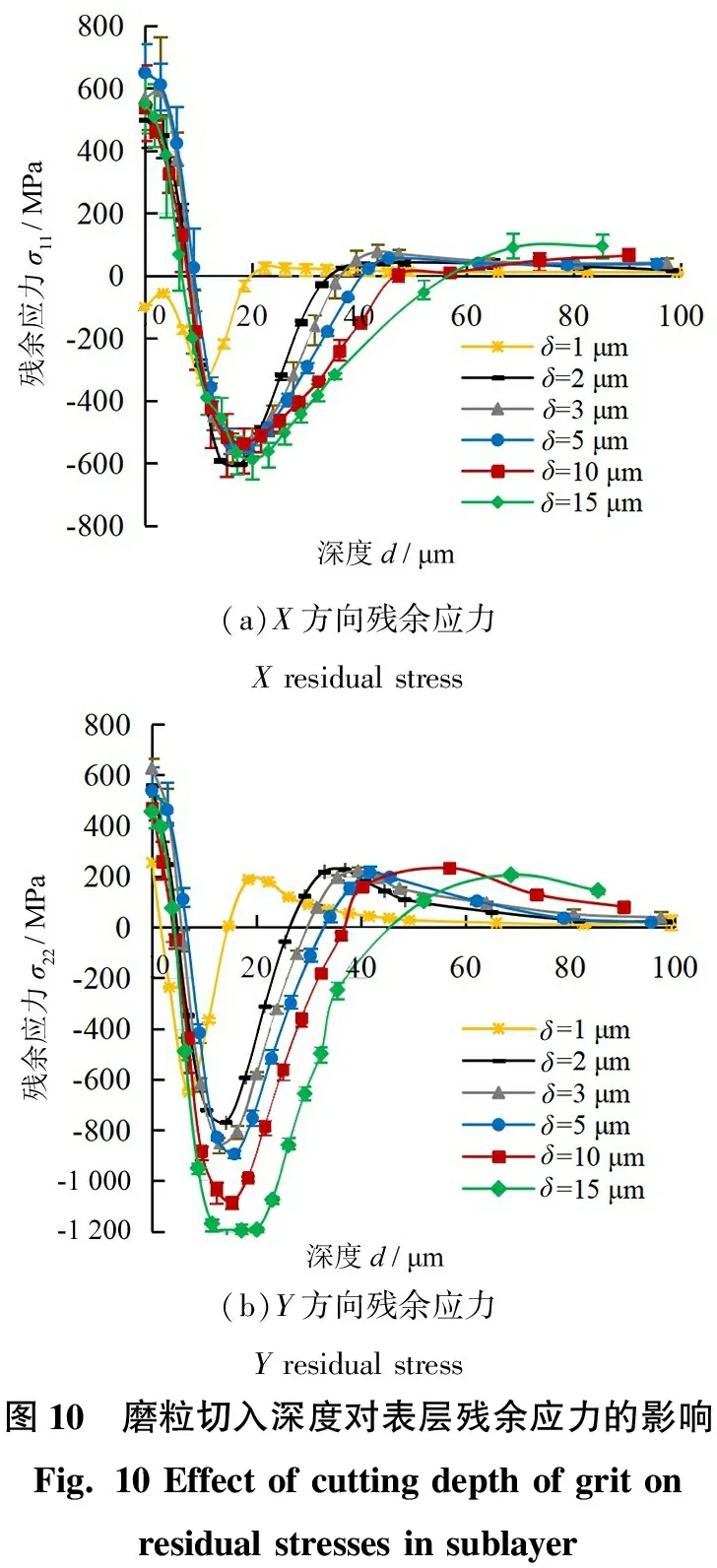
(a)X方向残余应力X residual stress(b)Y方向残余应力Y residual stress图10 磨粒切入深度对表层残余应力的影响Fig. 10 Effect of cutting depth of grit on residual stresses in sublayer

图11为不同切入深度下表层温度的变化。由图11可看出：划痕温度和热影响区的范围随δ的增大而增大，但表面温度的增长速率逐渐减小，这可解释上述残余应力的分布和变化规律。当δ=1 μm时，表面的σ11为压应力，而σ22为拉应力。其原因可能是材料沿划痕方向的挤压对残余应力的影响大于摩擦力和摩擦热的影响。反之，由摩擦力和磨削热产生的σ22拉应力部分仍占据主导地位。此外，图10b显示，随着δ的增大，σ22的残余压应力峰值和影响范围也增大。

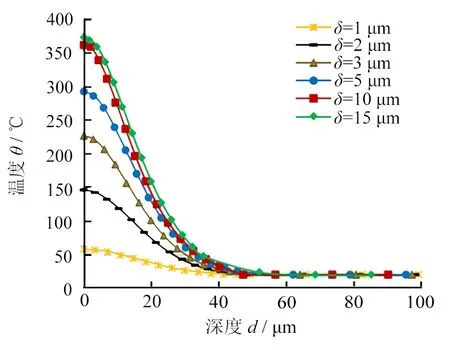
图11 不同切入深度下表层温度的变化

2.4 切削速度的影响

图12为工件表层残余应力分布受磨粒切削速度影响的变化规律。

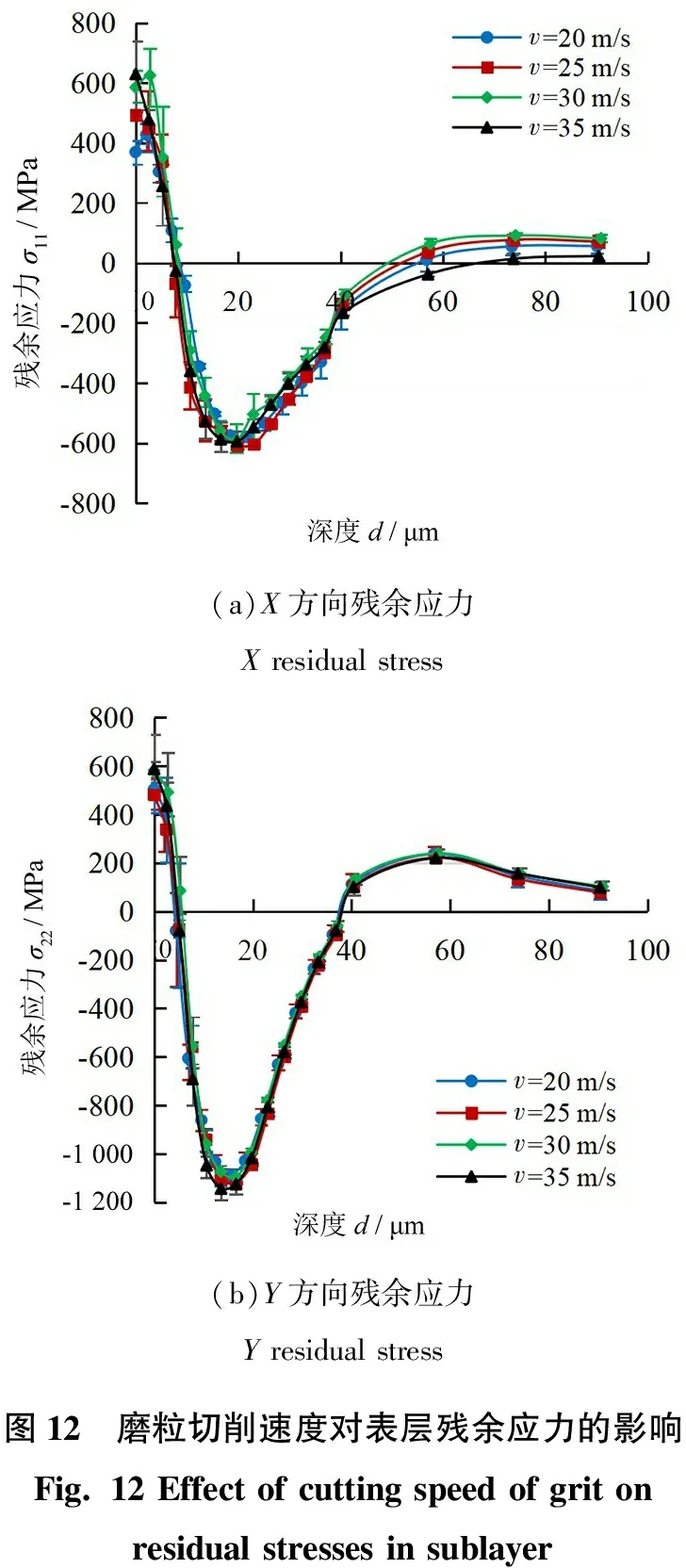
(a)X方向残余应力X residual stress(b)Y方向残余应力Y residual stress图12 磨粒切削速度对表层残余应力的影响Fig. 12 Effect of cutting speed of grit on residual stresses in sublayer

从图12可以看出：相较于摩擦系数和切入深度，切削速度对残余应力的影响最弱。不同磨粒切削速度仅对划痕最表面和大于40 μm深度的工件残余应力σ11有所影响，而对σ22的影响则几乎可以忽略。图12a表明工件表面σ11随v的增大而递增。这可能是由于磨粒切削速度增大导致了摩擦热流密度的增大，使划痕表面温度升高(如图13所示)，进而使σ11呈拉应力且幅值有所增长。σ11在较深处(d>40 μm)残余压应力上的差别未体现出随v变化的单调性规律，应力曲线误差限彼此也互有交叉，可认为v在此深度范围内对σ11的影响仍然微弱。

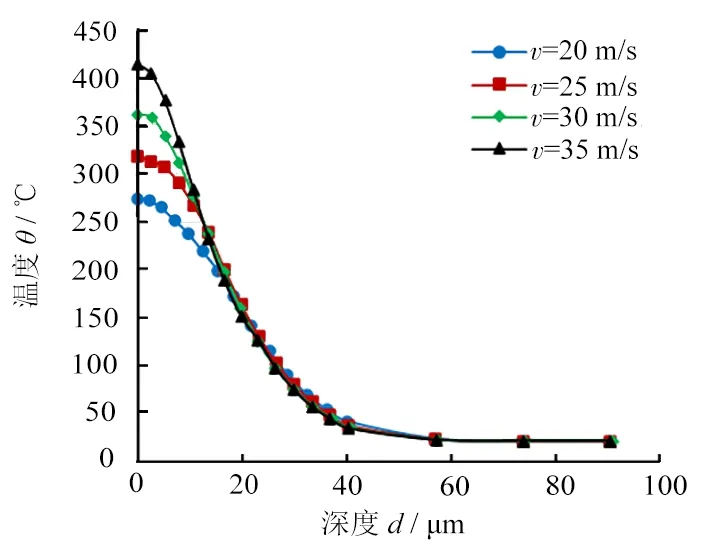
图13 不同切削速度下划痕中线位置表层温度的变化

此外，从图13还可发现：相较于其他因素对划擦温度的影响，切削速度变化对划擦温度在深度方向的影响范围更窄，大约为16 μm(其余接近40 μm)。因此，故其对残余应力的影响更局限于划痕表面，但这仍未能完全解释仿真结果中残余应力分布对于磨粒划擦速度变化所表现出的惰性。

根据以上规律，建议采用水介质冷却，优选低压、低速，磨粒粒度小的砂带。

3 结论

对磨削工艺参数对钢轨表面残余应力的影响进行试验研究，并进行单磨粒热力耦合有限元分析。主要结论如下：

(1)钢轨表面打磨后的残余应力在磨削方向上以拉应力形式存在，大小为100～300 MPa；而钢轨表面另一正交方向主要以压应力形式呈现，在0～-250 MPa波动。随着接触压力和砂带速度的增大、列车速度的降低，磨削方向上的拉伸残余应力幅值相应增大。

(2)通过有限元分析探讨了接触面摩擦系数、磨粒切入深度和切削速度对磨后轨面残余应力分布的影响规律。为获得较低的表面残余拉应力，依据所得规律建议打磨列车最后1组打磨单元采用磨粒粒度小的砂带，磨削工艺参数则应优选低压、低速，还可考虑增加水介质冷却和润滑。