大口径非球面镜交叉磨削中波纹度产生机理的研究*

席建普， 刘同士， 李亚东， 李 彬， 赵则祥

(中原工学院 机电学院， 郑州 450007)

大口径非球面镜由于其特殊的光学性能，越来越广泛地被应用到现代光学系统中，例如空间光学系统、激光核聚变装置、高能激光武器系统等[1-3]，对其表面形貌精度的要求也越来越高。大口径非球面镜大多是由硬脆性材料组成，其制造工艺过程包括粗磨、精磨和抛光3个阶段。其中的抛光过程可提高其面形精度和表面粗糙度，但抛光过程去除量小、效率低、周期长，因此磨削阶段保持适当的材料去除很重要，但抛光过程中的中频误差将影响到整个生产周期[4]。磨削阶段的非球面镜表面轮廓特征包括表面粗糙度、表面波纹度和形状轮廓。表面波纹度如果在磨削阶段不能很好地被控制，抛光阶段的波纹轮廓则难以被高效去除，这将严重影响非球面镜的加工效率[5]。

国内外学者通过建立表面粗糙度形成机理预测模型，仿真分析了非球面镜表面粗糙度的影响因素[6-8]。且磨削表面波纹度的研究也受到学者的关注。BIERMANN等[9-10]主要针对钢件磨削颤振引起的表面波纹度进行研究，结果表明磨削工艺参数影响颤振大小和相移变化。盛晓敏等[11]分析硬脆性SiC平面磨削表面波纹度的影响因素，证明砂轮速度是表面波纹产生的主导因素。毕果等[12-13]分析了非球面磨削表面波纹度产生机理，并对非球面磨削过程中表面波纹的产生与加工工艺参数和磨削方式的关系进行了研究，结果表明选择合理的加工参数可以改善工件表面的波纹度。林晓辉等[14]根据光栅平行磨削加工方式对轴对称非球面表面粗糙度和表面波纹度的作用机理进行研究，并结合磨削试验验证了砂轮振动是波纹度产生的主要因素。CAO等[15-16]提出了砂轮表面形貌的仿真模型及其对工件表面粗糙度的影响，分析了磨削参数和砂轮振动参数对表面波纹度的影响，结果表明：调整振幅、磨粒大小和磨削参数可优化工件表面质量或给定参数可预测工件表面形貌。BADGER等[17]研究了砂轮的偏心对磨削表面波纹度的影响，根据磨削参数和砂轮偏心提出了预测工件表面波纹度模型，验证了砂轮偏心将影响磨削力、砂轮磨损、砂轮温度和表面波纹度。PAOLO等[18]为了分析工件表面波纹度，建立了在线预估模型及方法，分析了砂轮表面微波纹对工件表面的影响，并基于最小二乘法验证了加工过程中动态线性模型的可靠性。

以上研究都对工件表面形貌的形成机理进行了仿真分析，并证明磨削振动是产生工件表面波纹度的关键因素。而对于磨削主轴振动与表面波纹度的关系，以及磨削工艺参数与表面波纹度三维模型的关系研究较少。因此，可以从三维模型角度建立磨削主轴振动、磨削工艺参数与表面波纹度的关系，为磨削过程提供理论参考。

通过对交叉磨削方式下磨削大口径非球面镜的动力学分析，预测其表面波纹度在磨削阶段的分布规律，建立表面波纹度与磨削工艺参数之间的三维模型。首先，建立磨削主轴动力学模型，分析磨削振动产生机理和磨削振动影响因素；其次，根据磨削工艺参数分析表面波纹度三维轮廓产生机理，仿真分析磨削工艺参数对表面波纹度的影响和三维波纹度特性；最后，通过实际磨削试验，验证所建立的三维波纹度分布模型的合理性。

1 大口径非球面镜磨削加工方式

根据砂轮类型将大口径光学非球面镜在磨削阶段的加工方式分为盘形横向磨削、交叉磨削、斜轴点磨削以及杯型砂轮点磨削和非对称自由磨削等。而对于大口径非球面镜，其曲率半径大，采用交叉磨削方式可提高砂轮的接触面积，材料去除率高。

图1为大口径非球面镜磨削机床UPM900。磨削试验机床包括3个直线轴和2个旋转轴，交叉平行磨削方式时采用XZ轴插补以及工作台C轴完成非球面镜轮廓的磨削成形和精磨加工；磨削过程中砂轮的磨削刃能均匀地接触工件表面，降低了砂轮的磨损，提高了磨削的精度和稳定性。

XZ轴的直线运动轨迹根据NURBS生成插补路径，加工过程中XZ轴插补进给，磨削加工路径在工件表面表现为螺旋线轨迹，通过砂轮速度、XZ轴进给速度以及C轴旋转速度配合完成磨削过程。

磨削用砂轮为进口D25砂轮(金刚石颗粒尺寸25～32 μm)，其直径为400 mm，圆弧半径为90 mm。通过反复补偿磨削，形成高精度表面形貌，包括表面形状精度、表面波纹度、表面粗糙度。磨削过程中由于砂轮轴采用液体静压支撑方式，在磨削力作用下，砂轮轴将产生振动，从而影响工件表面质量。

图 1 大口径非球面磨削设备UPM900

2 非球面镜磨削表面波纹度产生机理

2.1 表面波纹度

表面波纹度是介于磨削表面粗糙度和几何形状之间的特征量，并且在抛光过程中难以去除。GB/T 16747—1997规定了表面波纹度的参数术语和评价体系，以及波纹度参数的评价方法。表面波纹度反映振动强度大小，可用波纹度算术平均值Wa、波纹度均方根值偏差Wq等表示[17]：

(1)

(2)

式中：h(xi,yi)为表面采样点的偏差值；xi和yi为采样点坐标值；M和N为采样的点数。

2.2 液体静压主轴振动模型

磨削表面波纹度主要是由砂轮与工件之间的相对振动造成的，包括磨削系统的强迫振动和自激振动。砂轮的强迫振动主要由其不平衡量引起，且由强迫振动引起的波纹度在工件回转方向可见连续的直线或窄带痕迹。而自激振动由再生效应引起，即砂轮磨削受力引起的振动，存在平动和摆动2种方式，从而产生磨削表面的波纹度，同时影响其表面粗糙度。

将磨削砂轮主轴系统简化为一个多自由度系统，其动力学模型如图2所示，磨削过程中由于砂轮的接触点均匀，可以将磨削时的磨粒合力近似为恒力。

图 2 磨削主轴动力学模型

图2中的磨削过程中的液体静压主轴可以看作一个刚体，即一个对称旋转轴的刚性圆柱体——刚性转子。主轴不平衡量引起的振动可换算成砂轮接触点的振动幅值和频率。刚体的质量为m，液体静压刚体3个方向的阻尼分别为cx、cy、cz，刚性分别为kx、ky、kz。牛顿-欧拉运动学方程表达了主轴刚体的平移和旋转运动自由度。主轴刚体在XYZ方向和3个空间中，存在3个平移运动和3个旋转运动。刚体质心O在惯性坐标系O(XYZ)与参考坐标系o(xyz)中的平移和欧拉旋转变换为振动平移和旋转角度。运动刚体存在5个自由度，3个沿XYZ轴的平移自由度，位移分别为x(t)、y(t)、z(t)，1个绕Y轴旋转变换为刚体的自由度，1个为XZ轴惯性坐标系的旋转自由度。表面波纹度主要是由主轴刚体的振动位移产生，因此，研究表面波纹度主要研究砂轮相对于工件之间的平移运动。

对于受迫振动，磨削过程中被磨削材料表现为硬脆特性，难以加工。磨削过程中磨具与工件的相互作用力产生了砂轮的相对偏心量，在高速旋转过程中产生振动。设质点o的偏心量e在X方向上，则偏心量坐标可表示为：

(3)

根据牛顿运动定律，在O(XYZ)坐标系中不平衡量的强迫力与磨削力作用时，由于Y方向的振动变换较小，只考虑X和Z方向的振动位移，主轴刚体平移运动方程为：

(4)

式中：ω为主轴转动角速度。

连续作用下的激励力可以简化为N个脉冲激励作用的叠加，通过拉普拉斯变换和拉普拉斯逆变换得到振动位移响应解为：

(5)

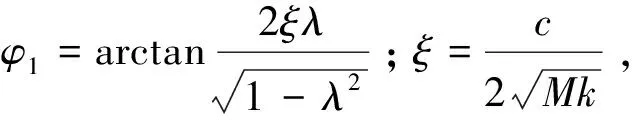
从式(5)中可以看出：主轴振动响应的位移大小与阻尼比、频率比和不平衡量有关。通过分析其幅频响应特性，可以了解系统稳态振动的振幅和相位差随频率变化的规律。磨削主轴的不平衡量可以通过测量或自平衡系统进行改进，以降低到最低水平。交叉磨削通过XZC轴的插补运动完成，因此砂轮存在振动形式如式(5)的正弦振动。

2.3 表面三维波纹度模型

张翊等[13]研究了微小振动对超精密磨削的影响，建立了主轴振动的余弦模型，并根据振动的模型分析了表面波纹的形成机理。CHEN等[7]假设砂轮主轴旋转中心振动的模型为正弦波形状，研究砂轮振动表面的粗糙度和亚表面损伤。以上研究都将砂轮的动态振动过程假设成一定幅值的正弦或者余弦振动。本研究中的砂轮主轴振动为正弦振动，交叉磨削过程中表面波纹的产生原理如图3。

图 3 交叉磨削表面波纹产生原理

图3中砂轮的中心在Z方向的运动轨迹为[15]：

z(t)=R+Asin(2πf0t+φ)

(6)

式中：A为砂轮振幅，f0为磨削砂轮轴的旋转频率，R为砂轮半径，φ为磨削砂轮的最初相位角。

在二维坐标系XOZ平面中，工件随X轴运动，为得到振动变化与x坐标的关系，沿X轴的坐标表示为：

x=fwfrt-R0

(7)

式中：fr为X轴进给速度，fw为工件旋转频率，R0为工件半径。

引入砂轮轴转动频率和工件转动频率比率：

(8)

式中：a为整数项，代表螺旋波纹的数量N；ε(0≤ε<1)为分数项。

将式(7)和式(8)代入式(6)。为模型计算方便，在以后的计算中可将砂轮磨削的最初相位角φ定义为0，得出砂轮振动表面轮廓：

(9)

因磨削过程中在圆周方向也存在角度位移，式(7)可表示为极坐标形式，角度随时间变化为：

(10)

式中：nw为工件转速，r/min。

联立式(6)和式(10) 得到：

(11)

式中：角度θ′=2πn+θ1，θ1为工件旋转的初始角度，n为工件旋转圈数。

工件旋转圈数相对位移为：

(12)

为更直观地表达磨削表面的波纹分布情况，需根据空间坐标点对磨削砂轮的振动轨迹进行离散处理。联立式(6)和式(7)消去t，且θ=2π(x+R0)/fr，θ为旋转角度，得：

z(θ)=R+Asin[θ(a-ε)]

(13)

将式(13)在圆柱坐标系P(r，θ，z)中表达，且随着加工的进行，极坐标半径减小为r时，θ=2π(-r+R0)/fr；同时，将整数部分a和分数部分ε分开，得到砂轮轴与工件之间振动形成的表面轮廓表达式：

(14)

式中：r为极坐标半径，随着加工进行极坐标半径增大。

将式(14)进行离散点处理，可得：

(15)

式中：N1为加工工件旋转的圈数，N2为每圈的角度Δθ等分数。

式(15)中描述的为磨削过程中砂轮在工件表面的离散路径。

2.4 磨削振动表面波纹度仿真

根据磨削砂轮运动轨迹，磨削过程中砂轮的振动将形成磨削表面的波纹度。从离散的轮廓公式(13)可以看出：三维的表面波纹度形成与砂轮转速、工件转速和X方向进给速度有关。图4为砂轮转速和工件进给速度对工件表面波纹度的影响仿真结果，固定磨削深度35 μm。其中图4a和图4b仿真时定义砂轮的振幅分别为4.0 μm和6.5 μm。砂轮主轴的振动频率f0=ns/60，工件轴转速频率fw=nw/60，将砂轮主轴转速和工件X方向进给速度作为主影响因素时，由图4可以看出：随着X轴进给速度增大，表面波纹度增大趋势明显，砂轮主轴振动幅值越大表面波纹度越大。因此，磨削工艺参数的合理匹配将直接影响到加工表面波纹度的大小。

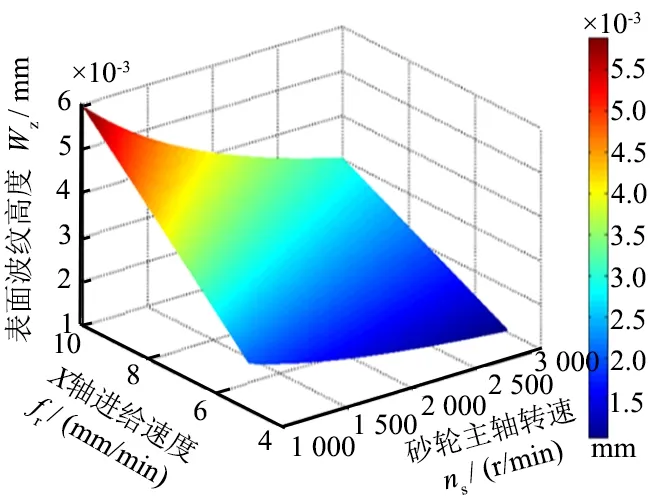
(a) 幅值4.0 μmAmplitude for 4.0 μm

(b) 幅值6.5 μmAmplitude for 6.5 μm

为了对离散的振动轨迹仿真分析，将交叉磨削方式的砂轮磨削点的运动轨迹定为螺旋线轨迹，因而Z轴的振动使磨削工件表面产生了空间波纹。根据式(14)对圆柱坐标进行分析，磨具与工件之间的相对位移关系与X轴进给速度、砂轮振动频率与工件转动频率比值有关，振动的幅值A与磨削过程的吃刀量有关。取砂轮的振动幅值A=0.005 mm，ε=0.3，fr=3 mm/r。当a=1时，得到砂轮振动产生的表面波纹度三维图如图5a；当a=3时，得到砂轮振动产生的表面波纹度三维图如图5b。从图5可以看出：a=3时的波纹条比a=1时的波纹条密，即a越大，纹路越多波纹度越大。

图6为砂轮的振动幅值A=0.005 mm，a=20，ε=0.4，fr=4 mm/r时砂轮振动产生的表面波纹三维图。从图6可以看出：波纹相较于图5变得更密，这是由于a值更大时，砂轮转动频率和工件转动频率比值增大，致使表面波纹产生的纹路较明显。且由于波长λ1(λ1=fr/ε)变化不大，基本符合所建立的模型。

根据以上仿真结果可知，在相同的磨削深度，振幅固定的情况下，要实现高的表面波纹精度，需要调整X轴进给速度、砂轮转动频率和工件转动频率，合理匹配磨削加工工艺参数实现高精度磨削。

(a) a=1

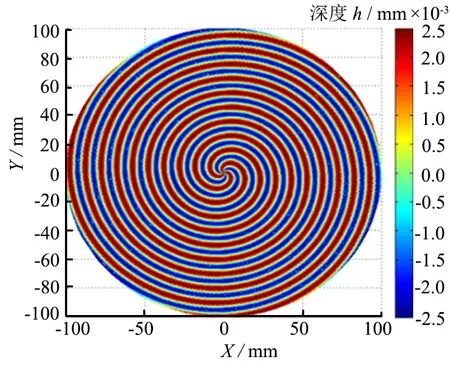
(b) a=3

a=20，ε=0.4

3 试验分析

利用四轴磨削机床采用交叉磨削方式加工大口径非球面镜，工件直径为320 mm，磨削工艺参数如表1所示。

利用Taylor PGI轮廓测量仪测量工件表面波纹值，通过对比同一区域的波纹度数值，分析表面波纹度

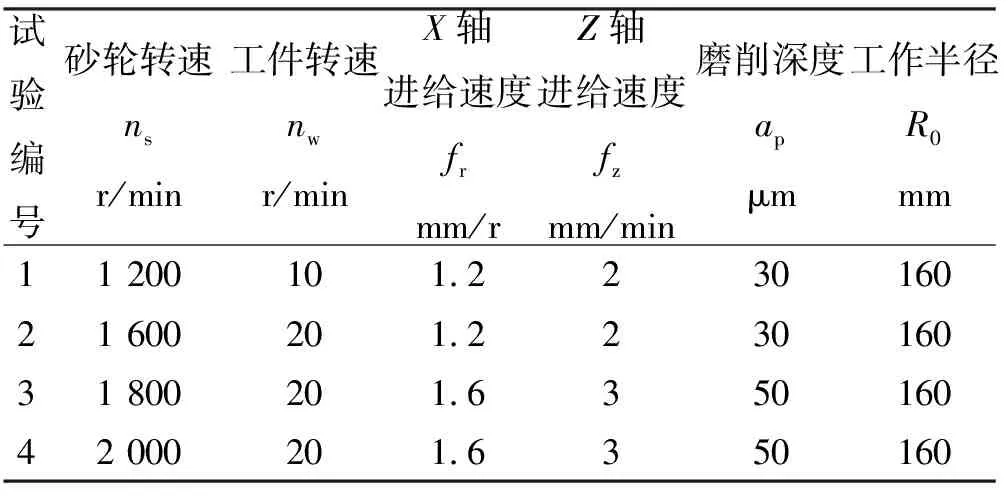
表1 磨削表面波纹测试工艺参数

与磨削工艺参数间的关系，研究最佳工艺参数区间。不同磨削深度下砂轮转速对工件表面波纹度的影响如图7所示。

图 7 不同磨削深度下砂轮转速对表面波纹度的影响Fig. 7 Effect of grinding wheel speed on surface waviness under different grinding depths

由图7可知：磨削深度为50 μm的表面波纹度大于磨削深度为30 μm的。这是因为磨削深度越大，振动的幅值越大，表面波纹度明显增大。且随着砂轮转速的增大工件表面波纹的大小呈非线性变化。当旋转速度达到1 600 r/min时，表面波纹显著减小；砂轮转速达到1 800 r/min时，表面波纹最小。根据砂轮磨削力公式可知砂轮转速增大磨削力减小，因此在砂轮转速从1 200 r/min增大到1 800 r/min时，振动幅值减小，所以表面波纹度减小；但当砂轮转速继续增大超过1 800 r/min时，砂轮偏心量增大，导致振动幅值增大，表面波纹也相继增大。由此可见砂轮转速为1 800 r/min，工件转速为20 r/min，X轴进给速度为1.6 mm/r是较优的工艺参数。

为了更好地验证模型的合理性，在砂轮转速为1 800 r/min，工件转速为10 r/min及X轴进给速度为1.2 mm/r条件下，采用交叉磨削方式进行表面波纹度分析，磨削后的工件如图8所示。从图8中可以明显看到加工后工件表面的纹路分布，且分布较均匀。该波纹主要由砂轮振动产生，并且从边缘到工件中心位置呈规律性弧形曲线分布。经统计，螺旋纹路值为181，该数值与模型中的砂轮转速与工件转速相除的整数部分一致。

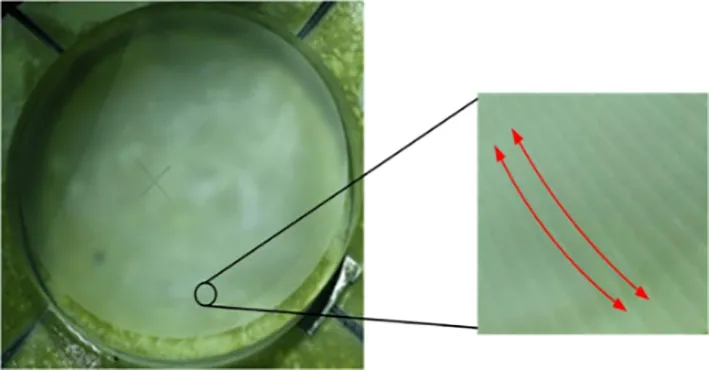
图 8 精密磨削后工件照片Fig. 8 Photo of workpiece after fine grinding

采用Taylor PGI3D轮廓测量仪测量磨削后的工件表面，取样长度为45 mm。图9是在径向方向测量的工件表面波纹度分布情况。由图9可以看出：工件表面波纹度幅值在5.8 μm左右，并且波纹的波长为1.3 mm。

4 结论

根据大口径非球面镜交叉磨削方式，分析了砂轮主轴由于磨削偏心产生的不平衡振动过程，建立表面波纹度形成机理的三维模型，并对表面波纹的形成进行仿真分析。

交叉磨削过程中，工件表面的波纹纹路是由砂轮主轴振幅、X轴进给速度、砂轮转速和工件的转速匹配决定的。仿真和磨削试验结果验证了建立的离散三维表面波纹度模型的合理性，并给出了最佳磨削工艺参数匹配范围为砂轮转速1 600～1 800 r/min，X进给速度1～3 mm/r，工件旋转速度20 r/min。采用此工艺参数可减小工件表面波纹度，提高抛光效率，实现大口径非球面镜的高效制造。