一道中考填空压轴题的命制过程及思考

江苏省江阴市第一初级中学 (214400) 钟珍玖江苏省无锡市堰桥初级中学 (214100) 魏 建

笔者有幸参加了无锡市2019年数学中考命题工作，其中填空压轴题(卷面第18题)的命制过程印象深刻，以下是命制过程及命题后的思考．

一、试题的编制过程

函数是初中数学的核心内容，函数思想是初中数学最为重要的数学思想之一，也是学生在高中阶段需要掌握的重要内容，图形的最值、定值问题是中考命题者非常青睐的考点，一线教师在中考复习中也会重点复习，其中尤其以线段的最值或者线段和差的最值是模拟试题中的“常客”，命题组决定考查有关函数的知识和思想，把二次函数、三角形全等、面积最值等问题集合在一起，综合考查．

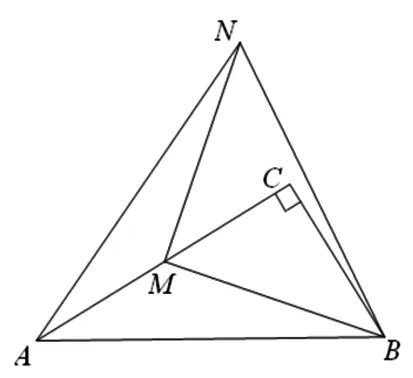
图1

初稿：如图1，在Rt△ABC中，∠C=90°，AB=5，BC=3，点M是AC边上的动点(不与点A、C重合)，连接BM，以BM为直角边作等腰直角△BMN，连接AN，则△AMN面积的最大值为．

题目考查了函数思想，凸显了符号意识，构造函数求面积最值也有一定的创新意识，命题组决定，试题的立意不变，改变问题的背景，问题的焦点在于当M运动到AC中点时，△AMN面积取到最大值，要想让学生不通过猜测，经过思考才能解决问题，考虑把直角三角形背景改为等腰三角形．

图2

图3

把二稿中的线段旋转90°改为以正方形来呈现，图形更加美观、匀称，更为重要的是作边AC的两条垂线，构造全等三角形，建立函数表达式的解题策略就更为隐蔽，需要学生有较强的图形识别和构造能力，提高试题的区分度.

从试题编制和修改过程来看，立意高远是试题优质的前提，反复打磨是出精品的保证，创新考法是试题有生命力的关键.

二、试题命制后的思考

1.试题编制，体现人文性

中考试题兼有毕业和选拔双重功能，要体现必要的基础性，也要有一定的区分度，有利于高中学段选拔人才，但试题的难易要适度，并不是难度越大越好，要避免试题的繁、难、偏、旧，重点考查学生对核心知识和重要数学思想方法的掌握和应用情况．所以试题的编制要让学生容易入手，有思考的切入点，从心理上有利于考生情绪的稳定，能较好地发挥考生的实际水平．本题题干精炼，叙述简洁，问题背景是等腰三角形和正方形，其背后隐藏着直角三角形，解决策略是作垂线构造K型全等，这些知识和方法学生比较熟悉，平时练习较多．求三角形面积的最值，也是模拟考试的热点问题，学生在审题和解答时，不会产生情绪波动，体现了对考生的人文关怀．真正体现了重点知识重点考，核心方法一定考．

2.试题编制，保障公平性

作为地区最为重要的考试，涉及到千万考生的切身利益，保证试题的公平性是命题时必须考虑的因素，所以中考试题要体现原创性原则，避免陈题的出现，影响试题的公正性．首先是试题的背景对不同地域和不同层次学校是公平的，试题的背景包括知识背景和应用题的实际背景，不论问题以何种方式呈现，学生对问题熟悉程度应保持一致性．在一次九年级上学期期末考试中，有这样一个填空题：一副有52张的扑克牌中，抽出一张牌是红心的概率是多少？笔者班级有两个非常优秀的学生，因概率题的背景不熟悉而失分．其次，所考查的知识和方法是课程标准要求掌握的核心内容，学生比较熟悉．

3.试题编制，凸显思想性

数学思想是内隐的数学知识，是数学的重要内容，是提高学生数学思维能力的重要抓手，一道好的数学试题，要能够考查学生的思维能力，体现数学本质．试题既要体现对考生的人文关怀，又要有一定的区分度，提高试题的区分度和效度.纵观无锡中考第18题的解决过程，学生必须要具有动态的意识，能敏锐地捕捉到在运动变化过程中线段长度、角的度数、三角形的面积等数学量的变化．首先要想到构建函数表达式解决问题，其次是要确定自变量，把△AMN的面积用自变量的代数式来表示，这就需要学生真正掌握函数的本质，及在运动变化过程中变量之间的依存关系，或者说学生只有理解了函数的本质，才会形成解题思路．学生比较熟悉的解题方法是给出自变量，再列出函数表达式，而本题需要学生自己确定变量，是试题编制的创新之处和亮点所在．问题较好地融入了函数思想、方程思想、符号意识等重要的数学思想方法，凸显以思维和思想立意的命题原则．

4.试题编制，关注导向性

毋容置疑，中考试题是本地区教师教学的“指挥棒”、“风向标”，必然会指引着地区数学教学的方向，所以中考试题的编制要符合数学课程标准，体现数学本质，贴近学生实际．试题的编制，要引导广大数学教师研究数学课程标准，知道课程标准的要求，知晓学生必须掌握的核心知识和核心思想方法，如本题所考查的知识：勾股定理、三角形全等、二次函数等都是初中数学的重要内容，所考查的数学思想：方程思想、函数思想、转化思想都是核心数学思想，是学生后续学习必须要掌握的内容．试题的编制要引导教师研究教学方法，试题的原创性和凸显思考性要求教师的教学要以能力立意，把培养学生的思维能力放在突出重要的位置，是数学教学最为重要的任务．数学教学不仅仅是解题教学，让学生记住解题模型解决问题，更重要的是通过数学内容的呈现和数学活动的设计，关注学生对数学本质的理解，本题的编制能有效考查学生思维能力，把教师的教学引导到研究课标、研究教材、研究教学、研究学生的正确轨道上．