知识衔接视角下一道平几题的解析与思考*

福建省莆田市教师进修学院 (351100) 林 伟

中学阶段的数学知识往往有着严谨的逻辑结构，它体现了数学知识的连贯性与整体性.在教学中重视知识衔接是对学生思维拓展和能力延伸的体现.本文以知识衔接视角从全等、相似、共圆、解析几何等方式呈现对一道平面几何题的解析与思考.

图1

1.试题分析

如图1,在ΔABC和ΔADE中,∠BAC=∠ADE=90°，AB=AC，AD=DE，连结EC,求∠BCE的度数.

本题为初中数学一道平面几何题，题目结构比较简单，以两个等腰直角三角形为载体，通过点D的位置需求∠BCE的度数.分析图形的结构特征，ΔABC为定三角形，而随着点D的运动，ΔADE的大小发生变化，从而带动点E的运动，由设问可知点E的运动轨迹应该在一条固定的直线上，所以可以求出∠BCE的度数.本题的适用范围广，可通过各个不同角度来解题从而渗透出平面几何各部分知识的联系与区别.

2.试题解析

2.1 从三角形全等的角度

图2

解析：如图2过点D作DF⊥BC交CA的延长线于F,由已知得AD=DE,又∠ADF+∠ADC=∠EDC+∠ADC=90°,所以∠ADF=∠EDC,在RtΔCDF中∠FCD=45°,所以DF=DC,所以ΔADF≌ΔEDC.即∠BCE=∠DEA=45°.

评析：本题欲求∠BCE的度数.从全等三角形的角度出发，ΔEDC中包含要求的∠BCE，构造与ΔEDC全等的三角形是本题的重点.在全等三角形中常以平移、对称、旋转做为解题的突破口，本题的解题就是以点D为中心把ΔEDC旋转90°构造于之全等的ΔADF.

2.2 从三角形相似的角度

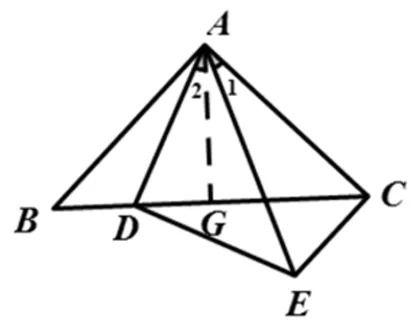
图3

2.3 从四点共圆的角度

解析：在RtΔABC中，AB=AC，所以∠ABC=∠ACB=45°.在RtΔADE中，AD=DE,所以∠DAE=∠DEA=45°.则∠DEA=∠ACB，所以A，D，E，C四点共圆，即∠BCE=∠DAE=45°.

评析：从四点共圆的角度来看，无论图形如何变化∠DEA=∠ACB始终不变，易判断出A，D，E，C四点共圆.共圆后利用同弧所对的圆周角相等可得∠BCE=∠DAE=45°，也可由∠ADE=90°判断出AE就是圆的直径，由圆内直径所对的圆周角为直角可知AC⊥EC.平面几何中圆知识的引入，更好的启发学生从图形的对称和点的运动来研究几何图形的性质.

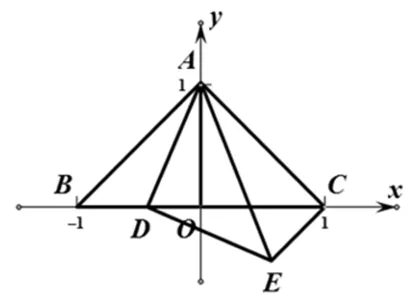
图4

2.4 从解析几何的角度

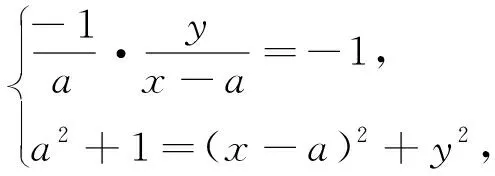
评析：本题易从直角三角形的结构特征入手，建立合适的平面直角坐标系.求出∠BCE的度数关键在于确定点E的位置,其中点D为主动点，点E为从动点，求∠BCE的度数其实就是确定点E的运动轨迹的问题.

3.追根朔源，启发变式

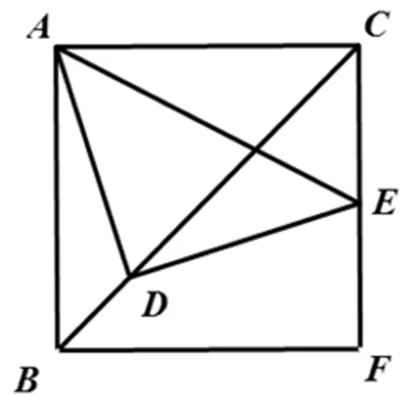
图5

根据几何图形的结构特征，采用补形的方法可以得到图像的载体为正方形.当点D在对角线BC运动的时候，点E的轨迹落在直线CF上.易得到其一个变式命题1：

如图5在正方体ABFC中，D在线段BC上，过D作AD⊥DE交CF于F，求证：AD=DE.

考虑图形的形状特征，只要保证两个三角形为相似的等腰三角形则点E的运动轨迹落在与线段AB平行的直线上.可得到其另一个变式命题2：

图6

如图6,在ΔABC和ΔADE中,∠BAC=∠ADE，AB=AC，AD=DE，连结EC,求证:AB∥CE.

4.解后反思

本文通过不同的知识点出发解题，在构造几何图形的补助线上有着较大的差异.从数学思想的来说，全等到相似是从特殊到一般的过程;从核心素养的培养来说，全等到相似是从数学抽象到直观想象深化的过程.全等是平面几何图形中基础的关系，全等可以看作是图形平移、对称、旋转变换的结果，这种变换保持图形的形状和大小不变.相似则是图形伸缩变换的一个过程，图形的形状不变而大小发生变化，要求学生有更高的直观想象能力;从数学知识与方法的衔接来说，平面几何到解析几何是几何与代数的融会贯通.