在数学探究中发展学生的逻辑推理素养

福建省闽清县第一中学 (350800) 徐杰霞

《普通高中数学课程标准(2017年版)》(以下简称《标准》)指出：逻辑推理是从一些事实和命题出发，依据规则推出其他命题的素养.主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳和类比；另一类是从一般到特殊的推理，推理形式主要有演绎.逻辑推理是得到数学结论、构建数学体系的重要方式，是数学严谨性的基本保证，是人们在数学活动中进行交流的基本思维品质.逻辑推理主要表现为：掌握推理的基本形式和规则；发现问题和提出命题；探索和表述论证过程；理解命题体系；有逻辑地表达与交流![1].课堂教学中，探究性教学是发展学生逻辑推理素养的重要途径.下面笔者结合数学教学实践，谈谈在探究性教学中培养学生逻辑推理素养的几点体会.

1.在结论的产生过程中引导学生探究，发展逻辑推理素养

高中数学对于学生推理能力的培养是在特定的情境中，要求学生尝试用数学的眼光去发现问题，解决问题.在课堂中，教师应提供素材，从知识产生和发展的切入点、思维的疑惑点精心创设问题，引导学生探索知识(概念、定理、公式等)的产生过程，让学生经历观察、猜想、证明的过程，使他们在实质性的思维活动获取数学知识，发展逻辑推理素养.

案例1 《普通高中新课程标准实验教科书·数学5(必修)》“正弦定理”的推理

必修5“解三角形”，是将学生初中学习的解直角三角形内容延伸到解任意三角.如何引导学生自然而然地获得“正弦定理”呢？下面是一次市级公开课的教学片断.

教学片断1提出问题，引导发现

问题1 在三角形中有大边对大角，小边对小角的边角关系.我们是否可以得到边、角之间的定量关系呢？

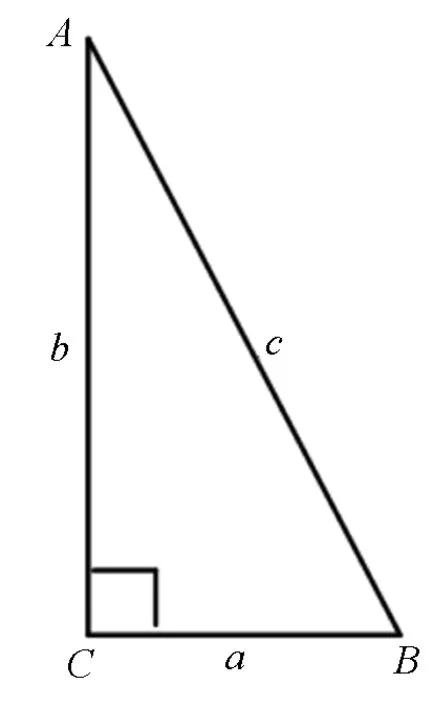
图1

师：我们可以先从特殊的三角形入手研究三角形的边角关系，大家想选择哪一类三角形呢？

生1：直角三角形.

师：同学们回顾一下初中学过的直角三角形的边角关系式.

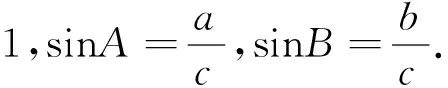
师(追问1)：以上两个等式有什么联系？

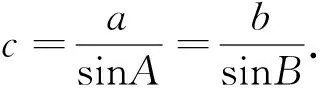
师(追问2)：以上等式含有角A、B，若等式也含有角C，那就更完美了，大家有什么想法？

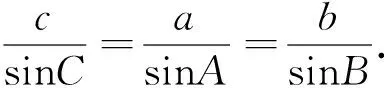
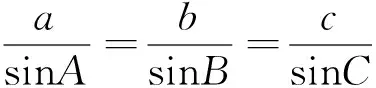
教学片断2类比猜想，分析证明

师：以上等式对正三角形能否成立？对内角分别为30°,30°,120°的等腰三角形能否成立？(学生验证成立)

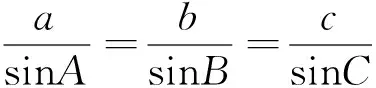
(学生思考、讨论、猜想.)

教师用几何画板演示，学生观察：边角的数据虽然在变化，但三组比值总是相等的，验证了猜想的正确性.

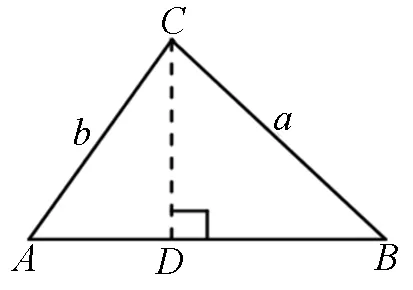
图2

师：怎样证明对于任意三角形，以上结论也成立呢？

(学生探究)

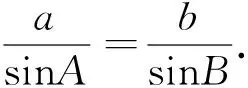
师：思路清晰！图2是锐角三角形,若ΔABC为钝角三角形的情况，请大家完成.

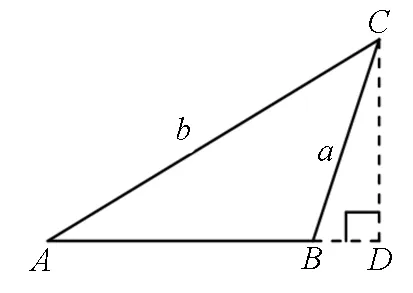
图3

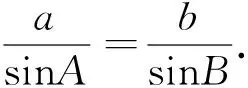
问题3 请探究正弦定理的其它证明方法.(限于篇幅，略)

在课堂教学中，教师应鼓励学生大胆、合理地猜想，这样不仅有利于开发学生的智力，加速新结论的形成，而且能让学生逐步掌握推理的基本形式，形成有论据、有条理的思维品质，发展学生的数学抽象、逻辑推理等核心素养.本课例从正弦定理产生的源头出发，宏观地提出问题，引导学生从特殊的直角三角形出发，探究边角关系式，使定理的发现与证明水到渠成，学生在进行严谨的逻辑推理证明的过程中，体会到了特殊与一般、转化与化归、分类与整合等数学思维规律.这样在教师的引导下“再发现“的过程，省力、省时且立意高远，学生不仅得到了“正弦定理”，而且获得了解决一类问题的基本思路(从特殊到一般，先猜想再证明的一般思路)，提高和发展了自身的逻辑推理和数学运算等核心素养.

2.在数学运用中引导学生探究，发展逻辑推理素养

培养学生的逻辑推理素养没有捷径，必须立足课堂，贯穿于数学课堂教学的全过程，循序渐进、日积月累.教师在引导学生发现结论并进行证明之后，为了巩固新知，深化知识内涵，数学运用是课堂教学必备的一个重要环节.教师可设置一些恰当的问题，使概念、规律的运用过程成为学生主动思辩的过程，通过学生积极的、活跃的思维碰撞，促进学生对知识内涵更全面、更深刻的理解，促进知识能力的高效果正迁移，提升思维品质和解决问题的能力，发展逻辑推理素养.

案例2 《普通高中新课程标准实验教科书·数学5(必修)》“正弦定理”的应用(第一课时)

问题1 在什么条件下可以用“正弦定理”解三角形？

生1：已知三角形的两角和一边，能用正弦定理求解其他的边和角.

生2：已知三角形的两边与其中一边的对角，也可以用正弦定理求解其他的边和角.

问题2 已知ΔABC中，c=10,A=45°,C=30°,求a.

变式已知ΔABC中，c=10,A=45°,C=30°,解三角形.

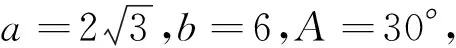
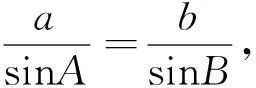
师：以上解法正确吗？

学生思考、讨论.有的学生觉得是对的，有的认为不正确.

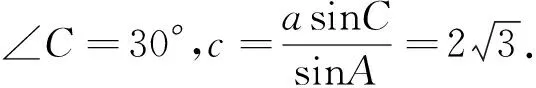
师：生4考虑问题很严谨，大家验证一下以上两解是否都满足条件？

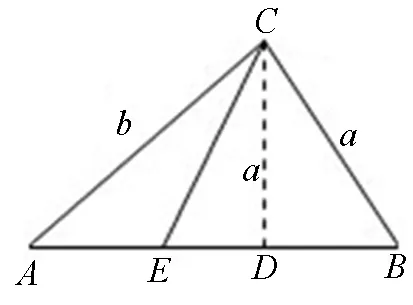
图4

生5：如图4所示，作CD⊥BA,D为垂足，在RtΔCAD中，CD=bsinA=3

师(追问)：能把它拓展到一般情形吗？

问题4 已知a，b，∠A，解三角形，如何判定解的情况？

(学生跃跃欲试，又开始了探究.)

生6：如图4，假设b≥a，当bsinA=a时，有一个解；当bsinAa时，无解.

师：总结得很到位！解三角形时，如果已知两边与其中一边的对角，可以先判定解的情况.

学生对“正弦定理“的认识是在探究学习和运用过程中不断发展的，因此在定理的运用阶段，教师精心设置问题，对学生进行逻辑推理训练，能培养学生的发散思维能力，培养学生分析、解决问题的能力，形成有条理、合乎逻辑的思维品质和严谨、求真的理性精神.

3.2 动物行为的获得途径 教师导言： 在我们生活的地球中，有数百万种动物，有的翱翔天际，有的驰骋大地，有的潜行水底，每种动物都有其独特的行为。它们的行为是如何获得呢？

3.在解题的反思中引导学生探究，发展逻辑推理素养

著名数学家波利亚曾说过：“数学问题的解决仅仅只是一半，而更重要的是解题之后的回顾与反思.”在解决问题后，引导学生反思，这不仅仅是简单的回顾或检验，更是对解题过程的深化与提高，能促使学生对问题的认识从感性层面上升到理性的高度，从而使学生的数学思维提升到由例及类的档次，有助于创新思维的培养与创新能力的形成，发展逻辑推理素养.

(1)求椭圆C的标准方程；

(2)E、F是椭圆C上的两个动点，如果直线PE、PF的斜率互为相反数，求证：直线EF的斜率为定值，并求出这个定值.

完成了本题后，教师有意识得引导学生对题目进行反思：

同学们也感到好奇，开始了探究.

反思3：椭圆有上述结论，双曲线、抛物线会不会也有类似的结论？

学生经过探究，得到了如下性质：

由上述结论可以得到圆锥曲线统一的一个优美性质.

性质4 已知点A是圆锥曲线C上一个定点，点E、F是曲线C上的两个动点，若点P和曲线C的一个焦点的连线与曲线C的对称轴垂直，且kPE+kPF=0,那么|kEF|=e.

通过层层递进式的反思，引导学生在探究中感悟、内化解题经验，能使学生掌握的知识更具广度和深度，使知识产生“连锁反应”效应，并生成新的问题“生长点”，逐步培养学生运用数学抽象的思维方式思考并解决问题的良好习惯.

毋容置疑，数学逻辑推理素养的发展不可能是一朝一夕之功，而是一个持久的系统工程，教师应为学生数学核心素养的发展创设时空，引导学生亲历数学化的思维过程，感知数学魅力，从而积极主动参与数学学习活动，让数学逻辑推理素养落地开花！