一体两翼蕴精彩，数形双飞显妙趣——基于知识内涵、思想方法的平面向量解题策略探析

重庆市巴南区西南大学华南城中学 (401346) 夏文涛

《高中数学课程标准》指出向量是近代数学中重要和基本的数学概念之一，它是沟通代数、几何与三角的一种工具，有着极其丰富的实际背景[1].鉴于此，在全国各地高考数学试卷中，平面向量成为了必考内容，其考查形式灵活多样，时常出现内容新颖别致的题目，它们在考查基础知识和基本技能的同时，注重对分析问题和解决问题能力的考查.

向量进入中学数学课程是一个相对缓慢的过程，直达2003年我国颁布《高中数学课程标准》，平面向量才全面进入高中数学.此后初期高考中，平面向量的考查内容主要是向量的基本运算，突出向量代数运算公式的运用.随着课程改革的推进，平面向量的教学日益深入，平面向量广泛运用到代数、三角、几何等领域，这不仅使我们加深了对向量的认识，也拓展了解决代数、三角、几何问题的思路.与此同时，高考对平面向量的考查也逐渐发生变化,不仅重视对向量的基本运算的考查，还注重对向量的几何意义、向量应用、向量与其他知识的综合.对于这些问题的解决，我们运用向量的代数形式居多，特别是向量的坐标方法，因为向量具有完美的运算结构系统，能够使得问题的解决程序化，也正因如此，我们的向量教学和向量解题更多地围绕着基本运算公式、运算律而进行.其实，这样既不利于我们准确把握平面向量的知识内涵，也使得在学习向量的过程中失去了对数学思想方法的领悟.

1.平面向量的知识内涵与数形结合的思想方法

从向量的知识内涵上看，向量是一种具有方向的线段，集数与形为一体，既具有代数形式，又具有几何特征，即向量是数形的“一体”，而代数形式和几何特征是向量的“两翼”.一方面，作为代数的对象，向量可以运算，如向量的加法、减法、数乘、数量积等运算，并且在直角坐标系中存在坐标运算形式；另一方面，作为几何的对象，向量具有方向、大小，可以刻画角度、长度、面积、体积等几何度量问题.

向量内涵上的数与形的特点，也为数形结合思想提供了良好的载体.平面向量的代数运算、几何意义是向量作为数形结合良好载体的两大形式，在认识向量时，我们就有了数学思想方法的理论支撑，这也为解决向量问题提供了数学思想方法层面的理论依据.

2.平面向量代数运算和几何本质的融通性

2.1 向量加法、减法运算的原理是平行四边形定理

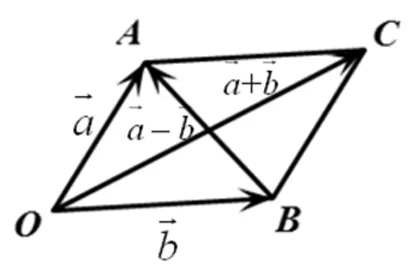
图1

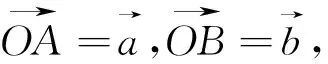
2.2 向量的数乘运算的内涵是线段的伸缩理论

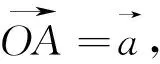
2.3 向量的数量积运算的内涵是余弦定理[5]

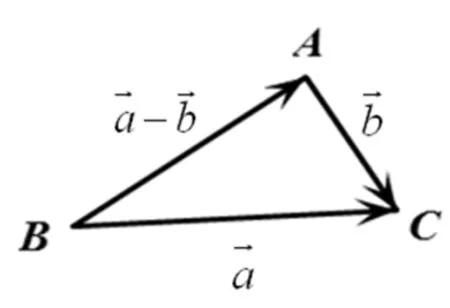
图2

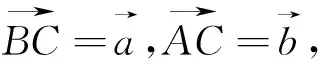
3.平面向量的解题策略

向量的数形特点沟通了代数和几何的联系，打通了向量与代数、几何、三角交汇的通道，也为高考向量的命题创新奠定了基础.数学解题策略是最高层次的数学解题方法，是对数学习题途径的概括性认识.戴再平教授认为就局部范围内的题目讨论，若涉及的知识有限，这个范围内题目的解题策略的个数将是有限的，我们可能通过逐一考虑这些题目策略，探索一般规律，归纳出一个逻辑化、模式化的方案，从而形成解题策略.[2]罗增儒教授在《数学解题引论》中指出解题策略具有四个基本特征：①普遍的适应性；②直接的可用性；③方法的二重性；④选择的最优性.[1]

基于以上向量知识内涵和数形结合思想，结合最近几年高考平面向量部分试题的特点，我们不难总结出满足以上四个特征的两大策略：

(1)从向量的代数形式出发，建立直角坐标系或选择恰当的公式，回归代数运算；

(2)从向量的几何意义出发，构造恰当的几何图形，转化为几何问题.

两大解题策略，各有优势，面对一个具体问题，可能要发挥向量的运算优势解题，而优势需要透过表象，揭示出问题的几何本质，以简化运算.这里，我们根据两大解题策略，通过对高考平面向量部分试题的分析和研究，总结出平面向量问题解决的基本思路和过程：

4.典型例题分析

根据以上平面向量解题策略，我们从全国各地的高考数学试题中选择出部分典型试题，从向量代数形式和几何意义两个方面出发，分别探讨问题的解决过程，从中体会两大解题策略的一些特点和规律.

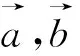
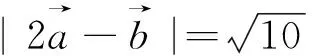
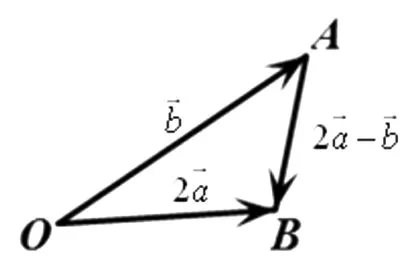
图3

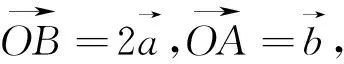
评注:解法1和解法2殊途同归，特别是①式和②式的相同性，很好地呈现了向量数与形的融通性.

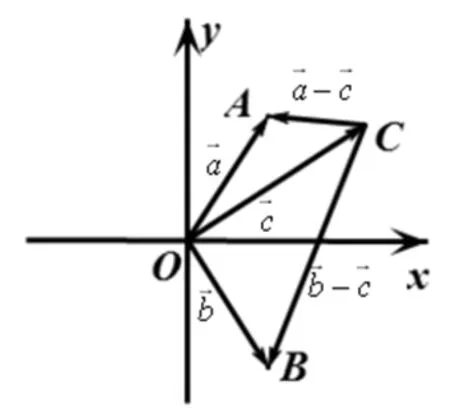
图4

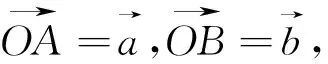
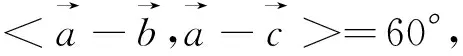
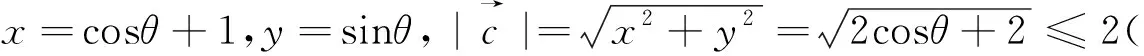
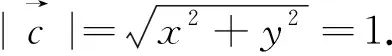
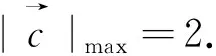
图5

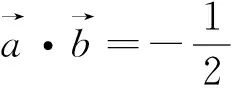
图6

评注:本题几何特征色彩重、代数运算难度大，是体现向量几何意义解题的经典试题.

5.思考与感悟

5.1 向量教学应该保持数形的统一性

数学课程应该返璞归真，努力揭示数学概念、法则、结论的发展过程和本质.在向量的教学中，我们一直重视向量工具性的价值，侧重向量的运算，突出公式的识记，而忽视向量内涵的提炼和升华.例如，从实用的角度出发，利用向量方法去解决几何、三角函数问题，如此固然可以体现向量的实用功能，但是一味地重复单一的方法，可能会影响学生创新思维的形成、创造能力的发展.

高中数学新课程倡导自主探索的学习方式，力求使学生的学习过程成为教师引导下的“再创造”的过程.向量“一体两翼”的数形特点，为学生提供了良好的学习探究平台.对课堂教学来说，以数形的统一性去引导向量教学，不仅有利于学生形成完整性的向量知识，也为向量在解决三角函数、平面几何等问题提供了知识基础.另外，数形的统一性也为向量的知识内涵上升到思想方法的高度提供了可能性，这样通过对向量数形的探索学习，学生通过数学教学获得的不仅仅是向量的知识内容，也经历了数形结合思想方法的体验.

5.2 向量的解题应该坚持策略的选择性

长期以来，高中数学的解题一直存在着“对题型，套方法”，通过“题海战术”，猜题押题的现象.对于平面向量，一些教师和学生认为记住公式就行，遇到向量问题就套用公式，或者见到几何问题，建立直角坐标系，或者解完题后缺乏反思，满足单一方法，误以为是“通法”.其实，平面向量具有数形融通性的特征，这既是向量内涵的题中之义，也是数学思想的必然结果.

跳出平面向量解题的单一、僵化的定势思维，从向量内涵、数形结合的角度审视平面向量，回归知识本源，体现数学思想，这样不仅丰富了数学知识，提炼了数学思想，发展数学能力，也不断提高了数学素养.解题策略的选择取决于实际解题实践的需要，解题实践丰富和发展解题策略，二者的结合是数学解题的内在要求.向量两大解题策略，各有其优势，兼具有不足，具体的选择应根据实际问题的特点而取舍，这样就超越了解题策略本身，体现了数学解题思维的发散性、灵活性、创新性.