设计合适情境 发展核心素养

上海市复兴高级中学 (200434) 方长林

教育部于2018年颁发了《普通高中数学课程标准(2017年版)》，《标准》提出了数学学科核心素养，“在学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析的数学学科核心素养”.基于核心素养的高中数学课堂教学，《标准》中的教学建议指出：教学活动应该把握数学的本质，创设合适的教学情境，引发学生的思考与交流，形成和发展学生的核心素养.数学知识只是素养的媒介和手段，知识转化为素养的重要途径是情境.情境可以有效地调动学生学习的积极性，进而很快进入学习状态；情境可以激发学生的学习兴趣，从而引发学生主动地探究；情境可以使抽象的、枯燥的知识产生丰富的依托点，让“冰冷的数学”变成“火热的思考”.情境化教学策略，是培育学生核心素养教学的一个重要的策略.因此数学教学活动中，我们应该结合教学内容及其蕴含的数学核心素养构建合适的变式情境(现实情境、数学情境、科学情境等)，引导学生用数学的眼光观察现象、用数学的思维分析问题，用数学的语言表述问题，有效地发展学生的核心素养.

1.设计实验情境，用数学的眼光观察世界

数学实验就是为了获取某个数学结论、验证某种数学猜想，在教师的引导下，学生通过动手操作，动眼观察、动脑思考，主要以“做”为支架，在思维活动的参与下进行的一种探索、研究活动.实验过程中，学生主动参与、提出问题、探究结论，不仅有情感的体验，而且实验中的操作、观察与思考，正是用数学的眼光观察世界，形成数学抽象、直观想象的数学素养.而这里“用数学的眼光观察世界”中的“世界”其实就是“发现问题、提出问题”中“问题的来源”，指现实世界中的、科学中的、数学中的问题.

案例1 “椭圆的定义”教学片断

实验情境1:演示与观察：课前准备一个装半杯水的圆柱形玻璃水杯，将直立的圆柱形水杯慢慢倾斜，让学生仔细观察水面的边界的变化(从圆形到椭圆形)；动画演示用不同的平面去截圆锥侧面所得截面边界的变化(从圆到椭圆).引发学生思考：我们研究椭圆的定义(未知)不容易，能否“以退为进”，由圆的定义怎样改变条件得到椭圆的定义？

活动1：用一根定长的绳子(无弹性)和铅笔画圆.(将绳子两端固定于图板上一点，套上铅笔，拉紧绳子，移动笔尖一周即可)

活动2：用一根定长的绳子(无弹性)和铅笔画其他图形(两人一组).(开放的情境，不同组的学生会将绳子两端固定在图板上两个点，并且会不断调整两点间距离，套上铅笔，拉紧绳子，移动笔尖一周，观察笔尖的轨迹：不同的椭圆、线段).

活动3：思考、探究、合作、交流.

实验情境2:折纸实验

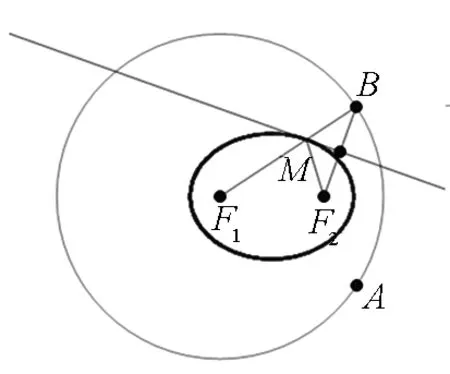
图1

(1)如图1，准备一张圆形纸片，标出圆心F1，在圆周上任取一点B，在圆内标出一点F2(异于圆心).折叠圆形纸片，使点B与点F2重合，将折痕与半径F1B的交点记作M.重复以上过程，得到若干个交点，观察交点形成的轨迹.

(2)几何画板动画演示折纸的过程.

设计意图:实验情境一：直观感知—动手操作—合作探究—概括定义.实验情境二：动手操作—思考探究—动画演示—概括定义.椭圆的定义如果直接告诉学生，那是知识传授式教学，不是指向核心素养的素养式教学.素养不是教的，而是在学科活动中形成的.要让学科知识与学生的思维活起来，首先必须让学生动起来.求知不是死记、硬背的过程，而是实践、体验、感悟的过程.离开了活动体验，知识是无法转化为素养的.实验情境一，设计从学生已有的经验出发，通过画图活动，经历从圆到椭圆的作图过程.并且从不同椭圆的作图过程中，思考探究，抽象概括出共同点：到两定点距离之和为常数(大于两定点间距离)，形成了椭圆的定义.情境的设计关注到数学抽象和逻辑推理素养.实验情境二，折纸实验让学生动起来了，形成椭圆定义的过程对学生转化和抽象能力要求较高，情境的设计关注到数学抽象和直观想象素养.具体教学中，两个不同的实验情境可以有机地融合起来，让学生深度参与到椭圆的概念教学中，以自主思考、探究的方式感受数学概念的生成过程，提升数学核心素养.

数学概念是数学思维的细胞，数学从根本上说是“玩概念”的，概念的产生常常包含了数学抽象的过程.椭圆定义的教学，两个不同的实验情境，抽象出椭圆概念，前一个是感性抽象，后一个是理性抽象，都是在实验过程中，用数学的眼光观察世界(数学抽象).因此实验活动是数学抽象素养形成的有效途径.

2.设计生活情境，用数学的思维分析世界

情境之于知识，犹如汤之于盐，知识需融于情境之中，才能显出活力和美感.生活情境即强调情境创设的生活化，主要联系学生的现实生活.现实生活是教学的源泉，只有在生活化的学习情境中，学生才能切实弄明白知识的价值.

案例2 “计数问题”习题课教学片断

生活情境1:匹萨饼店的伙计喜欢将薄底匹萨切成形状各异的一块块，他们发现，每一个确定的刀数，都可以有一个最多的块数．例如，切一刀最多切成2块，切2刀最多切成4块，切3刀最多切成7块，问切10刀最多可切几块？切n刀最多切几块？

生活情境2:蛋糕店的伙计喜欢将长方体形蛋糕切成形状各异的一块块，他们发现，每一个确定的刀数，都可以有一个最多的块数．例如，切一刀最多切成2块，切2刀最多切成4块，切3刀最多切成8块，问切10刀最多可切几块？切n刀最多切几块？

“数学源于现实生活，又用于实际生活”.创设恰当的生活情境，将有助于学生主动从生活中寻找数学模型，构建数学与生活的联系，从而养成用数学的眼光观察现实的思维习惯，发展数学建模、直观想象的数学素养.

3.设计问题情境，用数学的语言表达世界

著名数学家哈尔莫斯说，“问题是数学的心脏”；问题是开启数学之门的钥匙.没有问题就不会产生解释问题和解决问题的思想、方法以及相关的知识.没有问题也就难以诱发和激起求知欲，学生就不会深入思考，学习只能停留在表层和形式上.设计变式问题情境，激发学生积极地思考，主动地构建数学模型，用数学的语言表达世界(数学建模).

图2

案例3“基本不等式”教学片断

探究(1)正实数a、b的算术平均数和几何平均数可以分别用图中的哪两条线段来表示？

(2)能否从图中得出算术平均数和几何平均数大小关系？

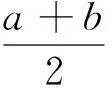
在数学探究教学中，无论是猜想的发现还是猜想的证明，都需要好的问题情境来引领，否则探究就无从谈起.数学家波利亚说：“不断变换你的问题情境”.设计有价值的、合适的变式问题情境，启发学生思考，引导学生把握数学内容本质.在进一步开拓思路、扩大视野的同时，潜移默化、润物无声地提升了学生的数学核心素养—用数学的语言表达世界(数学建模).

4.情境教学的一点思考

情境创设只是手段、不是目的，情境教学不能盲目成为一线教师追求的“时尚”.并不是每节数学课都能创设情境，也不是每节数学课都需要创设情境，更不是每节数学课所创设的情境都能起到良好效果.眼下，许多教师绞尽脑汁地创设各种情境(生活情境、问题情境、故事情境等)，似乎不创设情境，便显得自己的教学落伍.甚至经常出现为情境而情境的现象，煞费苦心地用情境包装教学.显然这是对情境教学理念片面的、甚至是错误的认识.当前，关于情境教学的确有一些问题值得我们思考，如情境的创设花哨而不恰当、情境的创设对学生的认知定位不准、情境的创设漠视学生的心理需求、情境的创设一厢情愿、牵强附会等等.因此，我们在创设情境时，要先问自己几个问题：一是情境与教学目标是否具有关联性；二是情境与新知识之间能否建立起有效联系；三是情境除了激发学生学习兴趣之外，能否真正诱发学生探究的欲望与动机、能否真正凸现素养教学(有效地发展学生的核心素养).我们不能取情境之“形”而忽视内容之“实”.

课堂教学中落实数学核心素养是数学核心素养落地的“最后一公里”，是数学教师培养国家未来人才的主阵地.基于数学学科核心素养的课堂教学活动应该把握数学的本质，创设合适的情境、提出合适的数学问题，引发学生思考与交流，引导学生用数学的眼光观察世界、用数学的思维分析世界、用数学的语言表达世界，促进数学学科核心素养的形成和发展.