点到直线距离公式的深入探究

天津市天津外国语学校 (300230) 高成龙天津市第七中学 (300162) 刘春红

课程标准的教学要求是探索并掌握点到直线的距离公式，在推导点到直线距离公式的教学中，教师应该从多角度引导学生思考，加强知识间的相互联系，培养学生的探索能力和创新意识.本文先给出教材(人教A版数学必修2)中的直线距离推导方法，再逐一给出其它证明方法，从多个角度来进行推导证明.

一、教材中的推导

教材中提供了两种思路来证明点到直线距离公式，即定义法和构造直角三角形法.

思路1：(定义法)所谓定义法是指过点P作直线l的垂线，垂足为Q，则线段PQ的长度就叫做点P到直线l的距离.关于定义法，教材中只提供了思路并没有给出详细证明，下面给出具体证明过程：

图1

如图1，过点P(x0,y0)作已知直线l:Ax+By+C=0(A·B≠0)的垂线，垂足为Q，将直线PQ与直线l的解析式联立求得点Q的坐标，然后利用两点间距离公式求得PQ的长度，即为点P(x0,y0)到直线l:Ax+By+C=0的距离.

由于直线PQ过点P且与直线l垂直，则PQ:Bx-Ay-Bx0+Ay0=0，与直线l联立得

由两点间距离公式得|PQ|=

点评：该方法通俗易懂，而且把点到直线距离公式转化成两点间距离公式，也是学生最容易想到的方法，然而不足之处是计算量较大，就连教材中也指出“上述方法虽然思路十分自然，但具体运算需要一定的技巧”.学生运用上述方法证明一般会遇到两个问题：(1)对于带参数的二元一次方程组求解可能遇到障碍，最终导致点Q坐标求不对；(2)利用两点间距离公式对最后结果化简时容易出错.

下面看教材的第二种思路：

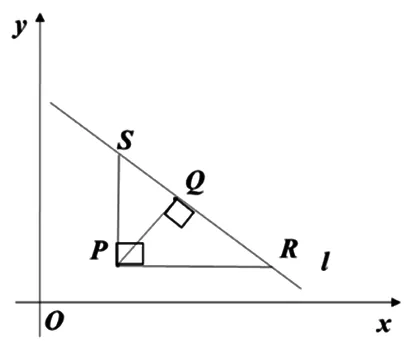
图2

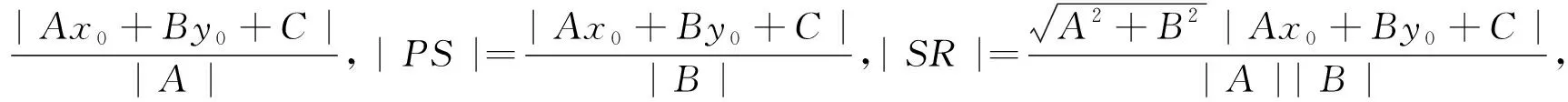
点评：利用等面积法求出点到直线距离公式，很容易接近学生的最近发展区.

二、公式推导再探究

下面通过设而不求法、解三角形法、平面向量法、等面积法、平行线公式法对教材提供的两种思路进行优化.

根据l⊥PQ且点Q在直线l上便有

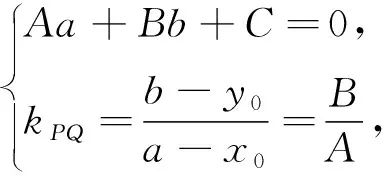
点评：设而不求法是处理解析几何常用到的方法，技巧性强，但的确降低了计算量，很好地体现了数学中整体代换的思想.同时利用该法证明点到直线距离公式为后续学习点差法求解圆锥曲线问题打下基础.

继续利用教材中构造的RtΔPRS，下面利用解三角形法和向量法对思路2进行优化.

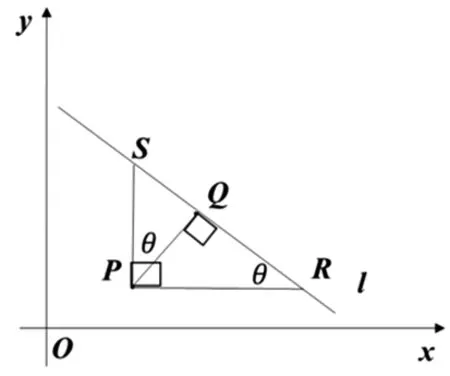
图3

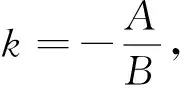
点评：思路4抓住了直线斜率的几何意义，利用斜率求得相应的三角函数值，把点到直线的距离|PQ|放到RtΔPQS中去，很好地把距离问题转化成了解直角三角形的问题，大大减少了计算量.同时很好地提高了学生解三角形的能力和对公式的进一步理解.当然也可以把线段|PQ|放到RtΔPQR中去，利用|PQ|=|PR|sinθ同样可以得到上述结论.

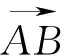
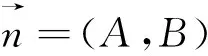
点评：利用向量法求点到直线距离公式的思路和方法很重要，事实上，我们还可以将上述思想和方法推广到三维空间，进一步求得点到平面的距离公式，这为我们后续学习向量法解决立体几何问题打下基础.

我们对思路2进行深入探究和分析，思路2利用等面积法求出点到直线距离公式，思路很好，很容易接近学生的最近发展区，然而其不足之处是计算量太大，尤其是求|SR|时利用两点间距离公式计算量非常大，学生容易出错，而|SR|不好求的本质原因是点S、R的坐标过于复杂，如果我们把三角形的形状和位置稍作改变，使得更多的顶点落在坐标轴上，同时把点P也平移到坐标轴上，这样问题就会变得更加简单，教学中教师要培养学生将复杂的数学问题转换成简单问题的能力.下面我们利用等面积思想将思路2的证明方法进行优化.

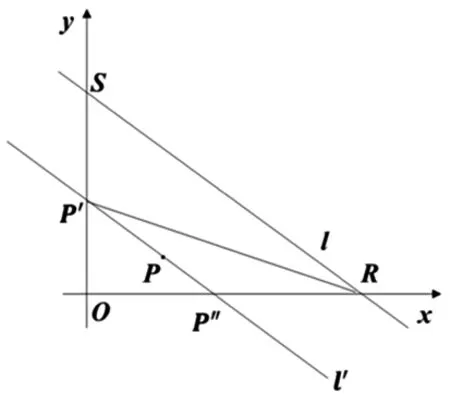
图4

思路6：(优化等面积法)如图4，过点P作直线l的平行线l′分别与坐标轴交于P′、P″，设直线l与坐标轴交于R、S，所以点P到直线l的距离即为P′与直线l的距离.

易知l′:Ax+By-Ax0-By0=0，所以P′(0,

点评：思路6的证明利用等面积思想把思路2中的点进行平移，把三角形进行特殊化，使得三角形的三个顶点都落在坐标轴上，这样大大减少了计算量.思路5当然也可以考虑ΔP″SR的面积，这里不再赘述.利用等面积法推导点到直线距离公式，思路清晰，过程简洁，符合学生的认知基础，不失为理想的证明方法.另外思路5的证明实际上给出了两条平行线的距离，把点到直线的距离转化成两条平行线的距离.

下面利用平行线距离公式推导点到直线距离公式.

思路7：(平行线距离公式法)对于平行线距离公式，教材只是以课后习题的形式给了结论.虽然教材中的例题涉及到平行线距离问题，但是教材中将其转化为一条平行线上的一点到另一条平行线的距离问题.也就是说教材将平行线距离问题转化为点到直线距离问题，如果我们逆向思维，把点到直线的距离转化为两条平行线的距离，是不是能让问题变得更加简单呢？下面我们先给出两条平行线距离公式及其证明：

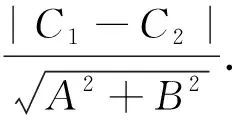
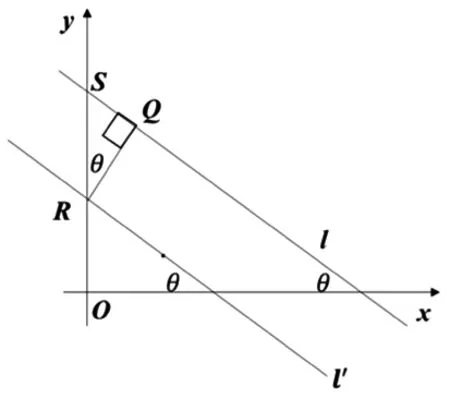
图5

点评：通过上面的证明发现思路7采取逆向思维，把点到直线的距离转化为两条平行线距离问题使得问题更加简单了，在证明过程中还给出了两条平行线距离公式.

三、教学思考与建议

从上面的证明可以看出，点到直线距离公式的推导有很多种.本文利用设而不求法、解三角形法、向量法、等面积法、平行线距离公式法对教材中的两种证明思路进行优化，让学生经历直线的距离公式的思维过程，深刻领会蕴含于其中的数学思想和方法，将点和直线放到平面直角坐标系中渗透数形结合、化归转化等数学思想.从多个角度进行探究，这正体现了高中数学不同模块之间的内在联系．

通过利用平行线公式法探究点到直线距离公式受到启示，有时候逆向思维可能使问题更加简单，因此在教学中要恰当的培养学生的逆向思维.在实际教学中可以先去探究平行线距离公式，然后利用平行线距离公式再去探究点到直线距离公式效果可能会更好.理由如下：第一，可以给出平行线距离公式，完善了教材的空缺，同时让学生在解析几何这一知识体系上更加完善；第二，证明平行线距离公式，为今后求解点线距离、线线距离提供新的思路和方法；第三，可以借助平行线距离公式去探究和证明点到直线距离公式，可以培养学生数学转换的思想和解决问题的能力.