安全扭矩约束下的多关节机器人轨迹跟随方法*

张少林，王 颖，王 硕

（1.中国科学院自动化研究所，北京 100190；2.北方重工集团有限公司，沈阳 110141）

在多关节机器人的工作任务中，不可避免地与外界环境发生接触。为了保护工件、工作平台，减轻对人员的伤害，常需要对机器人的关节扭矩进行约束，同时使机器人保持笛卡尔空间路径不变，实现设定的任务目标。另外，当运动指令的速度和加速度较大时，机器人关节电机不能提供所需要的扭矩，会产生冲击和振动。为了避免机器人的损坏，也需要对关节扭矩进行约束。因此，有必要对机器人在安全扭矩约束下的轨迹跟随方法进行研究。

针对多关节机器人的扭矩约束与轨迹规划已经有很多研究。在很多工业机器人上，通过在轨迹编程时对最大速度、加速度和加加速度等运动参数进行约束，使得机器人关节扭矩限制在一定范围之内[1]。但是，该方法中的参数设置需要依据经验，

不同的机器人和不同的轨迹需要设置不同的参数，不能直观地设置扭矩约束。为了直接限制各关节的扭矩值，可以在轨迹规划和插补完成后，对电机扭矩指令加以限幅，防止扭矩过大[2]。但是这类方法只在控制系统输出时将扭矩约束到制定范围内，没有同时考虑扭矩约束与轨迹规划。Zanchettin 等[3–4]将轨迹生成技术和优化控制策略合并到一个运动规划与控制的框架中，自主地分析程序指令给定的约束条件，实时地转换为运动命令，提高任务执行的可靠性。Yue 等[5]分析了扭矩约束时空间机器人控制系统的稳定控制策略。Valente 等[6]提出了一种在运动约束范围内生成平滑轨迹的方法，在装配过程的运动精度和速度之间达到平衡。这些方法在机器人的工作空间内搜索了满足稳定性、时间最优等控制性能的轨迹，但是不能针对笛卡尔路径主动地将扭矩约束到特定范围内。目前，一种常见的扭矩约束与轨迹规划方法应用在轨迹的最短时间规划方面[7–11]。该方法基于动力学模型分析关节最大扭矩限制，通过使至少一个关节的驱动扭矩达到最大来实现运动时间的最小化。通常，该方法先根据动力学模型计算各位置点对应的最大速度约束，形成位置–速度相平面的约束边界线。然后从起始点分析最大加速度对应的相平面曲线，从终点分析最大减速度对应的相平面曲线，并在边界线的极小值处求相切曲线，从而实现从起始点到终点的最短时间规划。另外，郭清达等[12–13]通过遗传算法计算了机器人在扭矩约束的情况下能够达到的关节速度、加速度和加加速度，从而实现在扭矩限制范围内的轨迹规划。但是，这类方法需要针对整条轨迹进行综合分析，计算量大，耗时较长，通常在计算完成后才开始运动。刘华山等[14–15]通过在控制过程中引入具有饱和特性的正反切函数来确保扭矩的有界性，并通过模糊自适应PD控制来减小超调量，提升轨迹跟随性能。但是，饱和函数的非线性特性可能对系统产生影响，不同函数的选取需要调节不同的控制系统参数。Dahl[16]通过对轨迹进行时间缩放来实现扭矩约束时的路径跟踪。该方法在原控制器基础上扩展了辅助控制器，控制系统较为复杂。因此，在保持多关节机器人的笛卡尔路径不变的同时，如何实时施加扭矩约束并保证快速轨迹跟随还需要进一步研究。

本文将对安全扭矩约束下的多关节机器人轨迹跟随方法进行分析，将机器人各关节的扭矩约束到指定范围内，继续按照笛卡尔空间路径运动，并使得机器人能够快速跟随指令轨迹，避免运动太慢引起的效率低下。该方法可以提升作业的安全性，达到保护机器人和作业环境的目的。具体将从以下几点进行分析：

（1）分析机器人轨迹上的动力学约束，依据设定的关节扭矩，重新计算最大加速度，使得机器人轨迹跟随不超过安全扭矩。

（2）在安全扭矩的约束下，实现对指令轨迹的动态跟随，达到实时计算与快速跟随的目的。

扭矩限制下的轨迹跟随

分析多关节机器人的受力为：

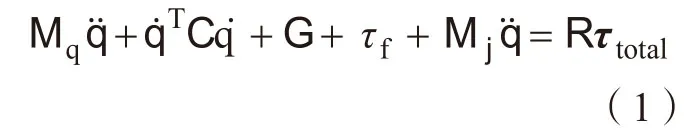
其中，Mq是质量矩阵，和是离心力和哥氏力，G 是重力，fτ是摩擦力，是关节惯性力，是电机提供的驱动扭矩是限制扭矩，q、是关节的角度值、角速度和角加速度。q 由关节位置传感器测量得到，通过对q 微分和滤波得到。在扭矩约束下，当机械臂的关节运动到位置q 时，和需要满足上式，以保证扭矩不超过限制值。

设机器人轨迹规划后，得到的运动曲线为s(t)∈R（t表示时间）。当关节扭矩被限制，不足以跟随指令轨迹时，应当保持路径不变，修改关节速度和加速度来满足扭矩要求。关节空间的位置、角速度和角加速度与曲线s(t)之间的关系如下：

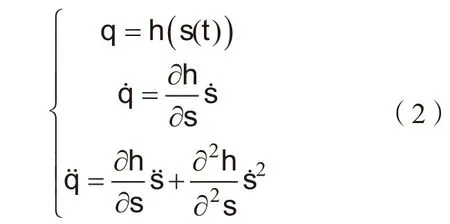
式中，h变换可以表示为h(s)= fInvk[fPos(s)]。fPos(s)∈R6为将长度s 映射到指令轨迹的笛卡尔坐标点，fInvk表示求运动学逆运算。

设曲线映射关系fPos(s)为

式中，P0为起始点，n为与长度s对应的曲线单位矢量。考虑到q=fInvk(P)，求导可得：

式中，Jb为雅克比矩阵。因此，由式（4）和式（5）可得：

由式（3）和式（6）可以推导h的导数为：

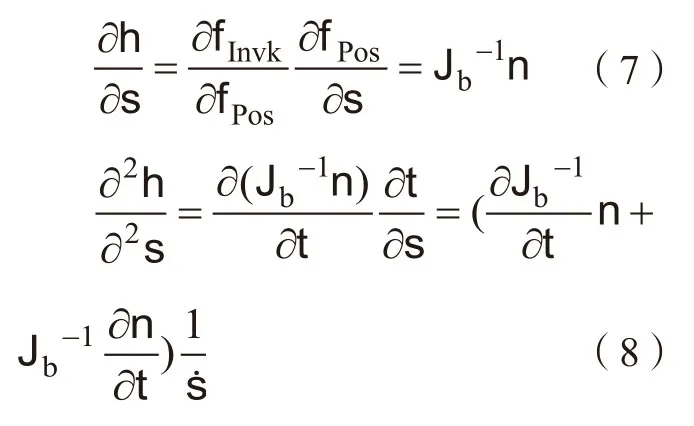
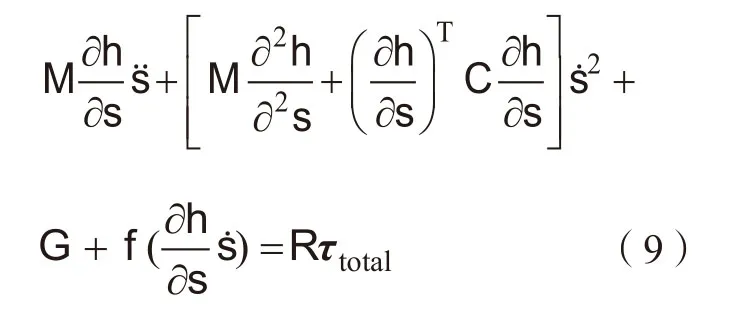
式中，M=Mq+Mj，和分别表示笛卡尔空间的速度和加速度。由式（9）可以得到和的约束关系为：

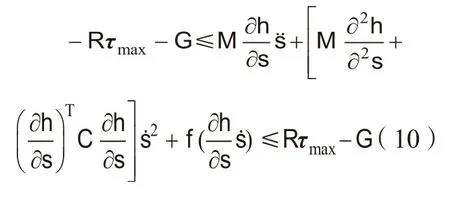
步骤1：设当前机器人状态为sc和。依据S型加减速[17]计算下一个周期的指令轨迹点sd、和。

步骤2：采用PID和前馈控制[18]计算下一个周期的笛卡尔空间位置、速度和加速度：

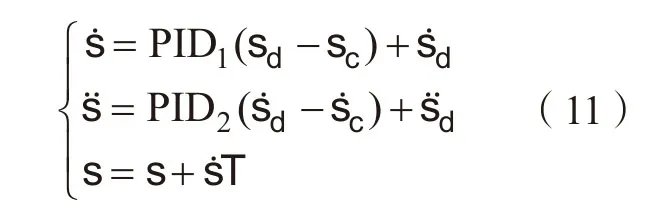
步骤4：比较τtotal和τmax的大小。如果则扭矩在限制范围内，跳转步骤6。否则，跳转步骤5计算扭矩约束。

步骤5：比较Rτtotal和Rτmax，判断是第几关节扭矩超限。依据式（10）求解此时的最大加速度s˙˙并积分得到和s。

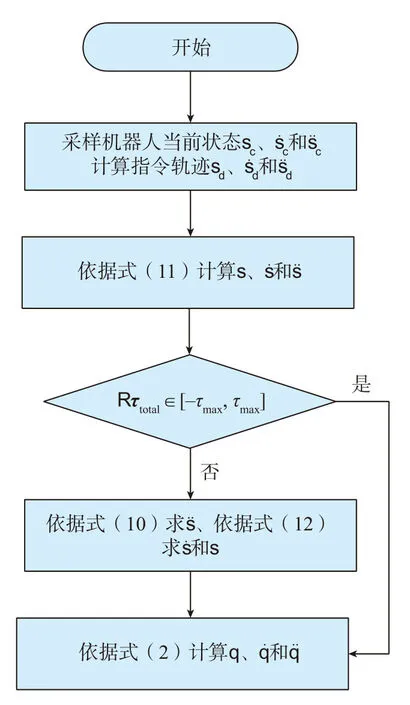
图1 扭矩约束方法计算流程Fig.1 Calculation flowchart of torque constraint method

跳转步骤3继续执行。

步骤7：等待下一个计算周期的到来，跳转步骤1，依次循环，直到轨迹运行结束。

试验与分析

1 试验平台

为了对所述方法进行验证，在如图2所示机械臂上进行了试验。该机械具有6个自由度，全部都是旋转关节。机械臂上选用了较大功率的电机，并将所有关节的驱动电机都布置在底座上，通过中间传动件驱动末端关节运动。为了减小连杆惯量，设计了紧凑的传动方式。该机械臂的技术参数如表1所示。机器人关节臂最大长度约为1m。6个电机的功率都是200W。不考虑基座时，机械臂重量为13.8kg，且重量都集中在底座附近。末端执行器最大速度超过8m/s。各关节的运动角度、额定转矩和最大转矩如表2所示。该机械臂为人机协作臂，为了提高协作时的安全性，需要对机械臂各关节扭矩进行限制。

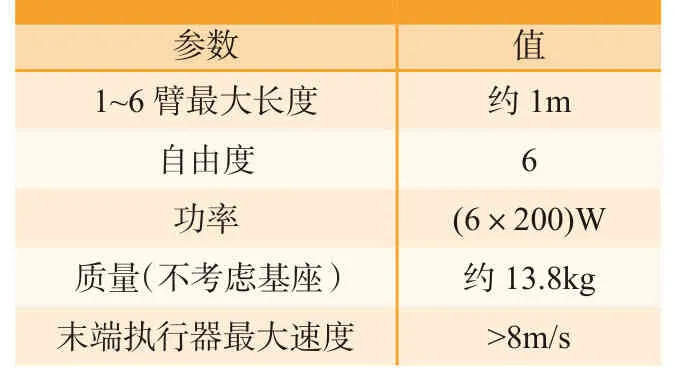
表1 机械臂技术参数Table1 Technical parameters of manipulator

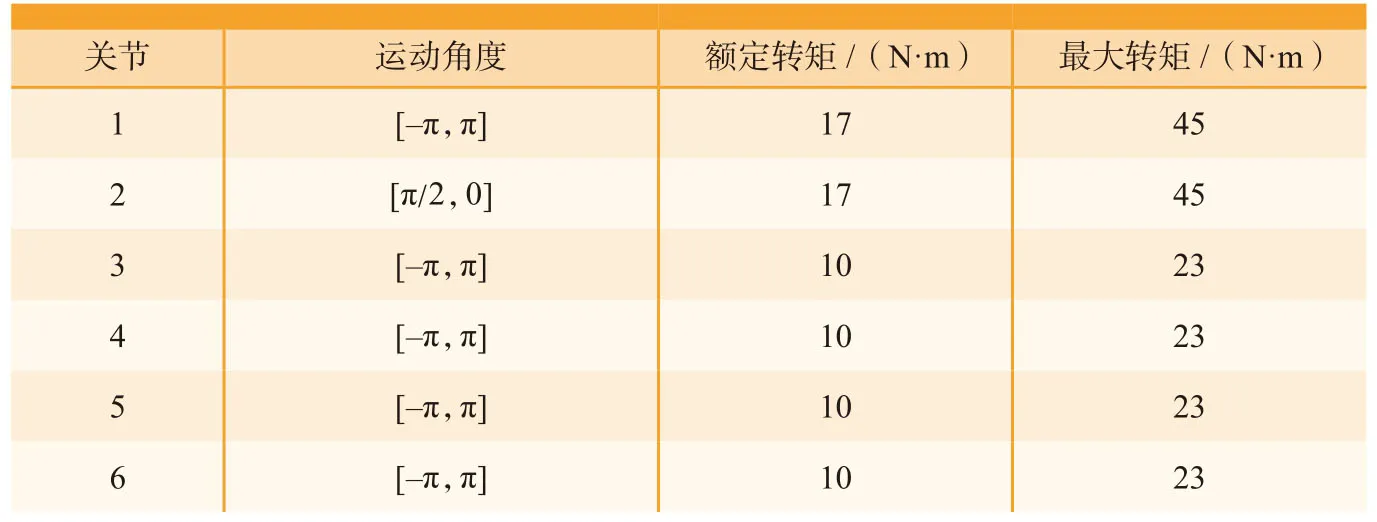
表2 机械臂各关节参数Table2 Joint parameters of manipulator

2 扭矩约束试验

为了验证机械臂是否在限定的扭矩范围内跟随指令轨迹运动，首先不限制关节扭矩，将如图3所示的笛卡尔空间直线段设置为指令轨迹，使机器人沿该轨迹运动。该轨迹根据S型加减速算法计算速度和加速。当机器人沿该轨迹运动时，采样电机电流并变换得到关节驱动扭矩，如图4所示。

图2 操作臂实物图Fig.2 Picture of manipulator

为验证扭矩约束方法的可行性，现以14N·m为例（即τmax=14N·m），将各关节扭矩约束到该扭矩范围之内，使机器人继续沿该轨迹运动并重新规划。图5为重新规划后的关节扭矩，可见，图4中扭矩1 超过14N·m的部分在图5中得到了约束，且在约束部分逼近14N·m。同时，为了保持路径不变，其他关节扭矩也相应变化。根据Chen 等[7–8]研究，当有关节的扭矩达到最大值时，其他关节的扭矩在最大值范围内相应调节可以使得机器人跟随指令轨迹，这种情况下沿着指令轨迹的运动时间是最短的。这种情况对应了扭矩约束时的最大加速度，具有最快的跟随效果。

重新规划的轨迹是基于运动曲线参数s进行的。该方法在原直线路径的基础上改变速度和加速度来实现扭矩约束，不改变原笛卡尔空间路径。因此，重新规划后仍然是如图3所示的直线段。图6为扭矩约束前后运动曲线参数s的对比（其中，蓝色虚线为扭矩约束后的s，红色实线为扭矩约束前的s）。虚线轨迹在N=100左右偏离了实线轨迹，这说明重新规划后速度和加速度发生了变化，与指令轨迹存在偏差。但是，虚线轨迹随后又快速跟随了实线的变化，这说明扭矩约束解除后，重新规划的轨迹快速跟随了指令轨迹。

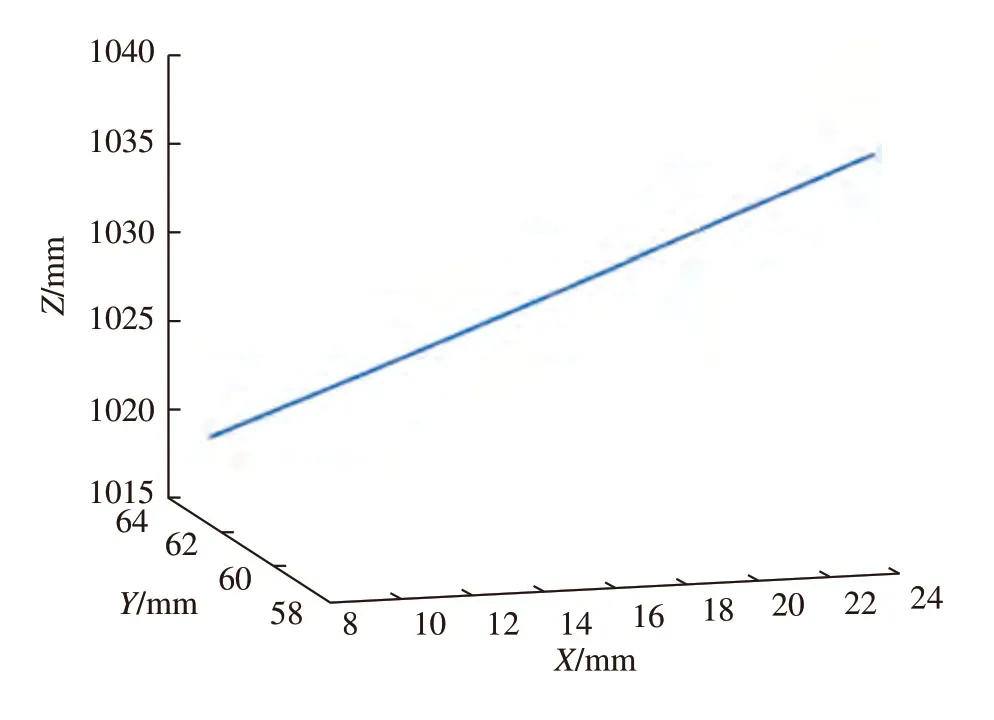
图3 机械臂指令轨迹Fig.3 Command trajectory of manipulator

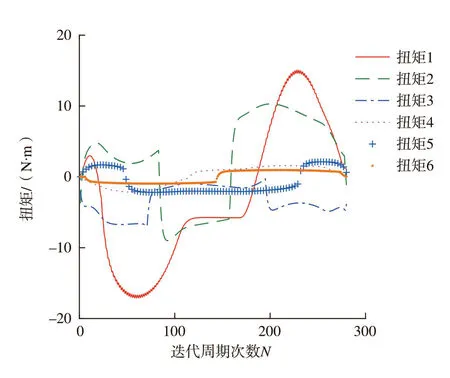
图4 指令轨迹对应的关节扭矩Fig.4 Joint torques corresponding to command trajectory

结论

本文给出了一种多关节机器人在安全扭矩约束下的轨迹跟随方法。该方法依据动力学方程约束，通过空间曲线参数s来保证笛卡尔空间路径不变，重新计算了当前允许的最大加速度，确保轨迹跟随过程不超过安全扭矩限制，提高了机械臂与人协作的安全性。同时，在安全扭矩的约束下，实现对指令轨迹的动态跟随，达到实时计算与快速跟随的目的。在六自由度自研轻量化协作机械臂上的试验验证了该方法的可行性。

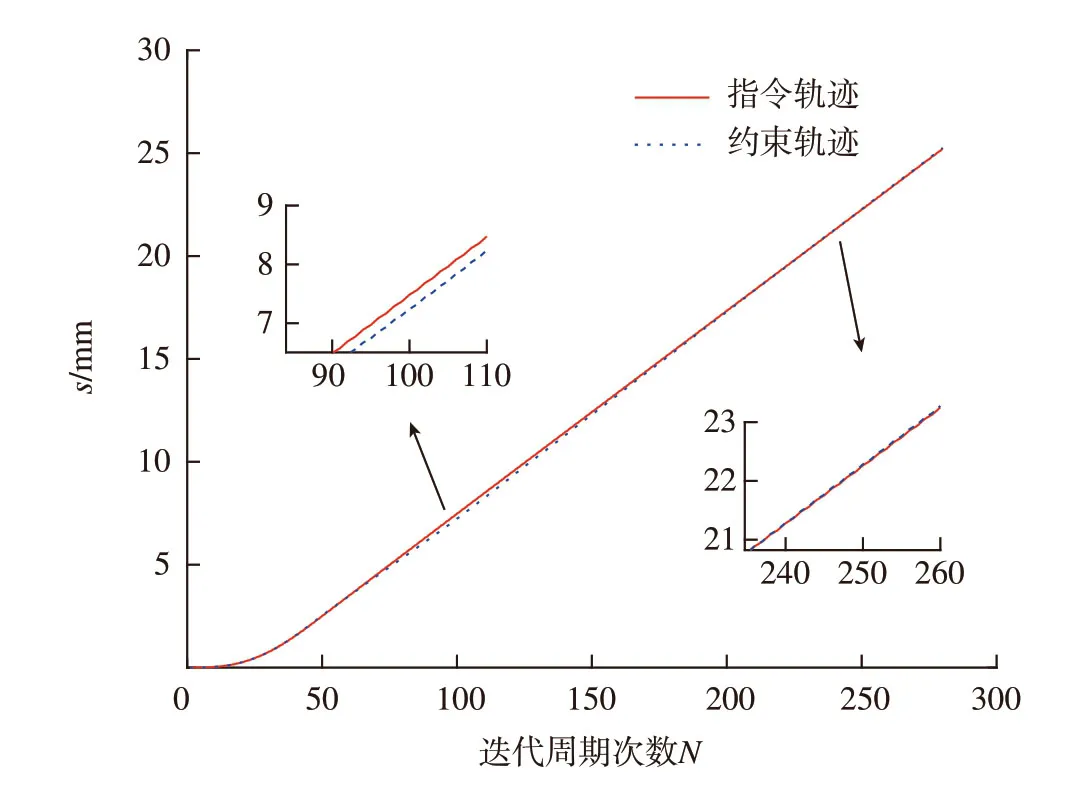
图6 指令轨迹与跟随轨迹Fig.6 Command trajectory and following trajectory