基于空气动力学的旋转球体飞行轨迹的计算模拟
2020-07-02赵炳炎陈宗华
赵炳炎 陈宗华
(玉林师范学院物理与电信工程学院,广西 玉林 537000)
在大学物理课程中,斜抛问题常被用来作为实例进行分析,分析时一般会把运动轨迹局限在竖直的平面内,并且将研究对象作为质点,根据牛顿定律分别在竖直和水平两个方向上建立动力学方程,有时还可以将空气的阻力考虑进来,最终得到两个独立的二阶线性常微分方程,求解可得出该斜抛运动的轨迹、最大射程、飞行时间等信息,这类问题已经成为质点动力学的经典例题。然而,从学以致用的角度出发,还有一些类斜抛问题受到广大学生的关注,比如足球运动中的“香蕉球”和棒球运动中“诡异的弧线球”等,这些现象显然与大学物理课程中学的斜抛运动是不符的。旋转的球体在飞行时,不仅受空气阻力的影响,还需考虑由旋转而引起的马格努斯力。但是由于旋转球体与空气的相互作用较为复杂,且动力学方程无法直接求得解析解,以往的讨论往往都局限在定性的描述或者简单分析二维的情况[1-5]。
本文通过对斜抛的飞行球体进行简化建模,将球体简化成质点并建立动力学方程,借助Matlab软件利用龙格库塔法对方程进行编程求数值解,从而模拟出球体的飞行轨迹。方程在三维空间建立,所以可以模拟出球体任意方向、任意旋转情况的飞行轨迹。这不但可以更好地帮助学生理解复杂曲线运动,还可以帮助专业体育教练指导球类运动训练。
1 旋转球体在空气中运动的动力学特征
球体在飞行过程中除了受到重力作用,还与空气有相互作用。其中重力作用的大小和方向都不变,记为mg,方向竖直向下。需要讨论的是球体与空气的相互作用,这涉及空气动力学问题,比较复杂,需要建模简化。可以将球体与空气的相互作用简化为空气浮力(该力方向始终竖直向上,可以归化到重力mg)、空气阻力FD和由旋转而产生的马格努斯力FM,其受力情况如图1所示。

图1 飞行球体受力图
1.1 对空气阻力的分析
由于球体的对称性,空气阻力FD与速度方向相反,空气阻力FD与球飞行速度的关系可以通过简化建模得到,如图2所示的圆盘为球体最大截面并与速度方向正交。
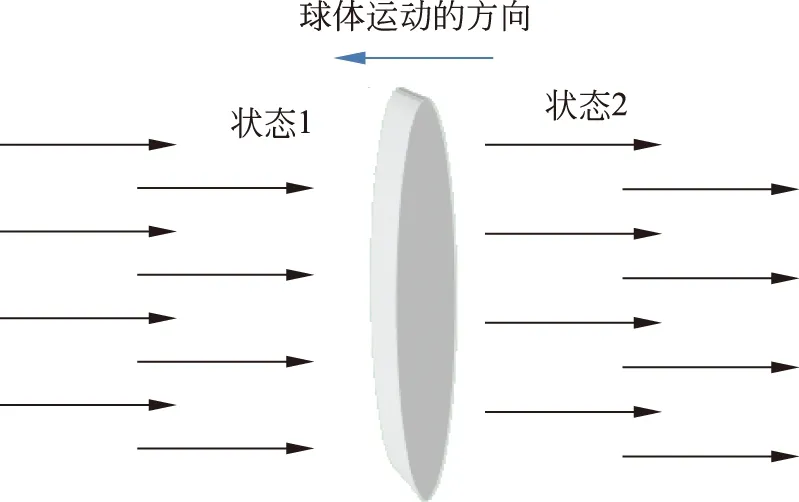
图2 圆盘两面气流情况图
如图2,圆盘两面所受到的压力不同,状态1为气流还未被球体穿过,压强为p1,相对流速v1=v。状态2的气流完全被圆盘遮挡,压强p2,相对流速v2=0。根据伯努利原理可得:
(1)
根据式(1),可以得到截面两边的压力差为
(2)
令圆盘面积为S,圆盘所受的阻力为圆盘两面的压力差:
(3)
式(3)是球体建模简化后的阻力关系公式。实际的球体并不是圆盘,空气会有速度损失,空气流过球体表面时会有摩擦力,而且球体旋转也会对球体阻力产生影响,实际的情况更加复杂[6-8]。本文引入空气阻力常数Cd来归化这些影响,在文献[6]~[8]中已经指出Cd不但与球体材料和表面结构有关,还与球飞行速度和转动速度有关,但是在本文中作为教学讨论,我们可以令系数Cd为一个常数,空气阻力可以表示为
(4)
其中,S为球体的最大截面;ρ为空气密度;为球的速度。如果空气密度不变,不考虑球体变形,则空气阻力只与速度的平方成正比,方向始终与速度方向相反。
1.2 对球体旋转引起的马格努斯效应的分析
球体旋转产生的马格努斯力来自于球体的各面流速不同所导致的压强差,这里以旋转轴方向与球速方向垂直为例,如图3所示。

图3 马格努斯力示意图
旋转的球体在空气中飞行时,旋转方向迎着气流一面的流速减慢,而顺着气流一面的流速加快,根据伯努利方程:
(5)
两面的压力差产生一个垂直于ω和的马格努斯力,其大小为
(6)
可以引入系数Cl使马格努斯力的表达形式与式(4)一致,并将马格努斯力的方向FM~ω×考虑进来,则有
(7)
式(7)中系数Cl的大小与球体表面结构、空气黏度、空气密度、飞行速度和旋转速度都有关[6-8]。为了不引起学生们的困惑,将它设为一个常数。
2 建立球体飞行的动力学方程
首先建立三维直角坐标系Oxyz,其中x轴和y轴为水平方向,z轴为竖直方向,根据牛顿第二定律建立球体飞行的动力学方程:
(8)
飞行过程中,角速度的方向可以分别投影到三维坐标轴上,有:
(9)
其中,
(10)
将球体动力学方程分解到各坐标轴方向上,得到3个二阶常微分方程:
(11)
其中,
(12)
该二阶常微分方程组是无法直接求得解析解的,需要用数值分析的方式来求数值解。我们采用Matlab软件包中四阶龙格库塔算法函数ode45对该方程组进行降阶计算。龙格库塔法求数值解必须给出初始条件,这里考虑球体在xz平面内由坐标原点出射,并假设球体射出后角速度ω保持不变。
3 以上、下旋和侧旋为例,得出轨迹图
在进行课堂讨论的时候,可以选择学生们比较感兴趣的足球进行讨论,相关参数设定可以在课堂上与学生们共同讨论得到。
设球体质量m=0.4kg,空气密度为ρ=1.29kg/m3,球体的最大截面积S=0.03m2,空气阻力常数Cd=0.35,升力系数为Cl=0.18。
为了方便讨论,设足球以45°在xz平面内踢出,踢出后的旋转角速度方向,分别以上旋、下旋和侧旋的情况进行讨论。
3.1 上、下旋的情况
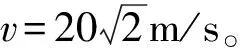

图4 足球上旋时的飞行轨迹图
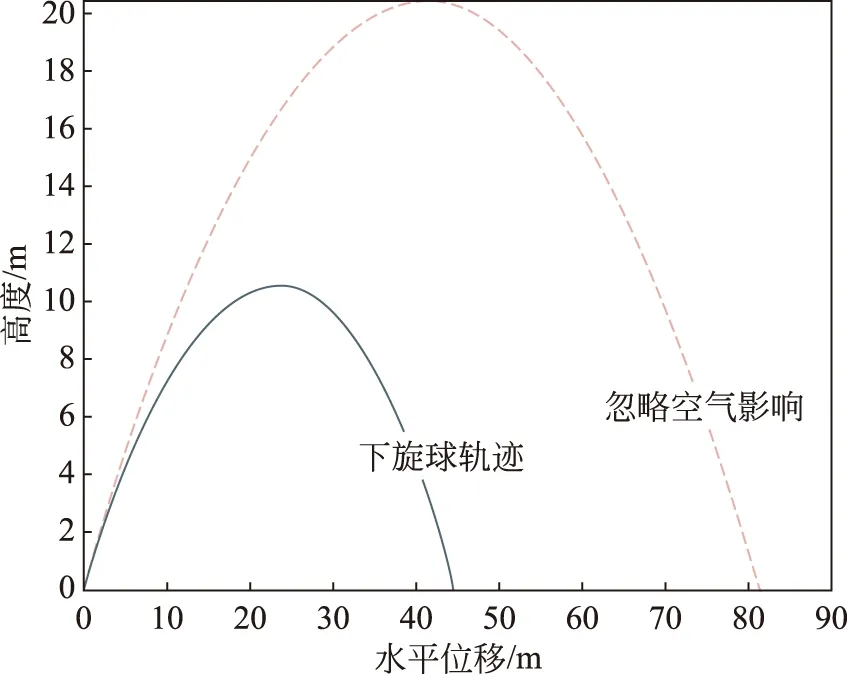
图5 足球下旋时的飞行轨迹图
从图4和图5的对比可以明显看到,空气阻力使得足球飞行的距离明显减小。但是上旋时的马格努斯力方向竖直向上,相当于抵消了一部分重力作用,足球飞行的距离较高。而下旋球受到的马格努斯力方向竖直向下,相当于加大了重力作用,足球飞行高度较低,甚至比上旋球低了近15m。由于上旋球在空中飞行的时间较长,所以水平飞行的距离也比下旋球要多出约12m,但是无论是上旋球还是下旋球的飞行距离,都明显比忽略空气影响时的距离要小得多。这也说明足球在飞行过程中,空气阻力和马格努斯力对飞行轨迹的影响非常大。
3.2 侧旋球的情况
侧旋情况是指,球体旋转角速度ω的方向与球体初始射出方向垂直,与速度方向顺时针成90°时定义为右旋,与速度方向逆时针成90°时定义为左旋,其他初始条件与3.1一致。
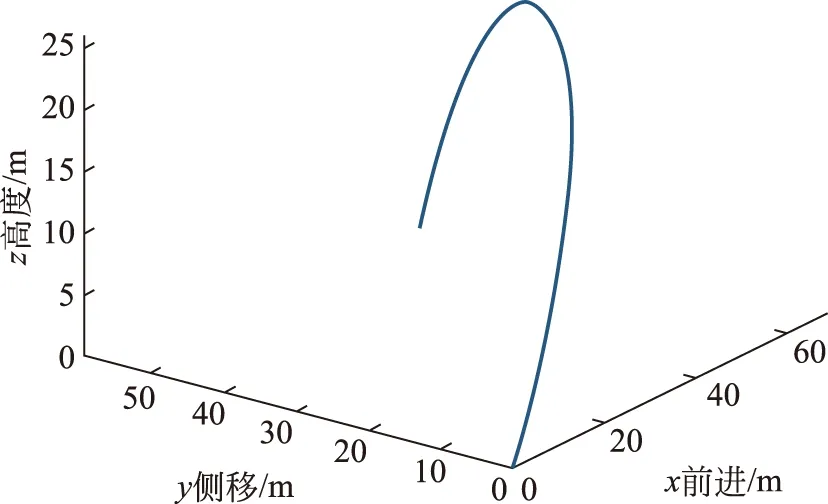
图6 足球右旋射出后的飞行轨迹
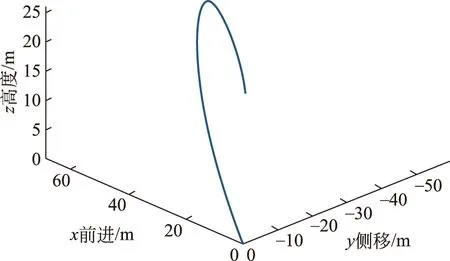
图7 足球左旋射出后的飞行轨迹
从图6和图7可以看到,由于足球旋转产生的马格努斯力,让足球飞行的轨迹发生了明显的偏转:右旋会让足球向左边偏转,左旋会让足球向右边发生偏转,这就是足球里经常说的“圆月弯刀”或者“香蕉球”。但是需要说明的是,实际情况中球体的旋转同样会受到空气阻力使角速度变小,而系数Cl和Cd也会发生一定的变化,所以实际上的偏转不会有这么大。
由图8可以看到完全的左右侧旋球在xz平面内的轨迹是一样的,这是因为侧旋时的马格努斯力是完全垂直于该平面的,它只能让球飞行发生转弯,产生所谓的“香蕉球”,而在球体前进方向上,只有空气阻力的作用,飞行距离一致。
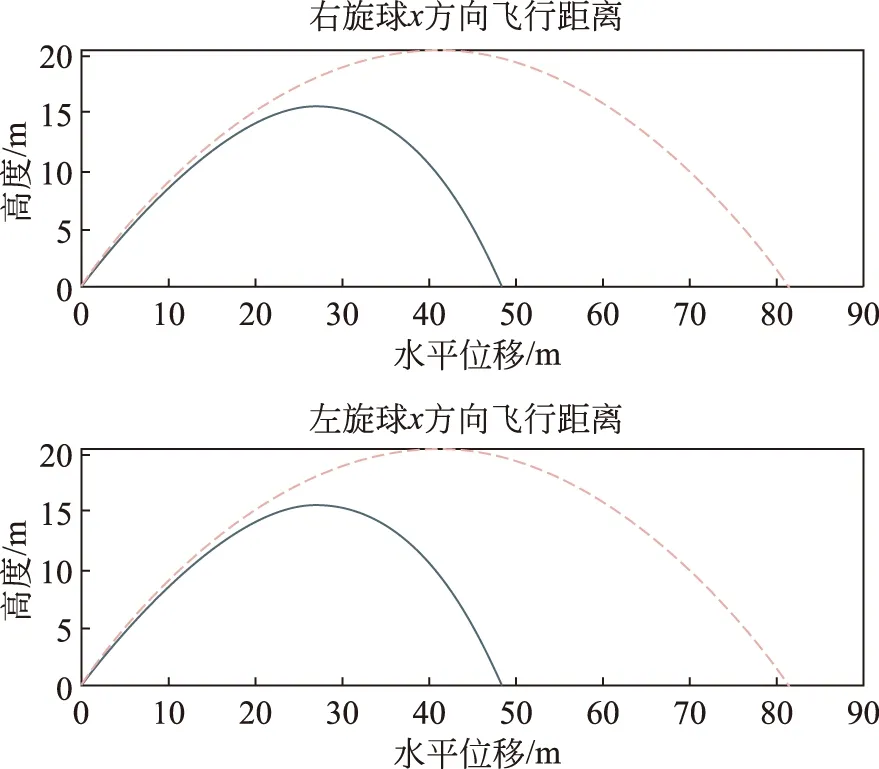
图8 侧旋球在xz平面内的飞行轨迹
4 结语
将贴近大学生生活的体育运动案例融入大学物理教学,既可以提升他们的兴趣,还可以培养他们应用物理理论分析问题和解决问题的能力。本文将飞行的旋转球体与空气的相互作用简化成一个空气阻力和一个马格努斯力,并将球体简化成质点模型建立动力学方程,且借助Matlab软件编程求解。以足球为例,计算模拟了足球上、下旋和侧旋的飞行轨迹,发现空气对旋转球体飞行轨迹的影响很大,这与足球运动时的实际情况基本相符。当然实际的球体飞行时,只有质点的动力学方程是不够的。球体本身还有旋转,而且这个旋转是可以绕任意转轴的,且球体旋转的变化也会导致空气阻力和马格努斯力的变化。要更准确地模拟出球体飞行的轨迹,有待更深入的讨论。
