求解次压缩算子分裂问题的自适应算法

贾倩倩，高兴慧

(延安大学 数学与计算机科学学院，陕西 延安 716000)

在本文中，设H1和H2是两个实Hilbert空间，〈·，·〉表示内积，‖·‖代表相应的范数，令S：H1→H1和T：H2→H2为两个非线性算子。分别用F(S)和F(T)表示S和T的不动点集，设A：H1→H2是具有自伴算子A*的有界线性算子，记ωw(xn)为序列{xn}的弱聚点集。分离公共不动点问题是寻找一点x∈H1使得

x∈F(S)且Ax∈F(T)。

(1)

注意到(1)等价于求解不动点等式

x*=S(x*-τA*(I-T)Ax*)。

(2)

对于分离公共不动点问题，许多学者都进行了研究，并取得相关的结论，参见文献[1-2]。最近，Yao[3]在Hilbert空间中引入了关于自适应算子的分离公共不动点问题的Halpern型迭代算法：

(3)

并在适当的条件下给出算法的强和弱收敛性。受上述工作的启发，本文给出了自适应算子在粘滞迭代下的强收敛定理，改进和推广了文献[3]及其他文献的相关结果。

1 预备知识

定义2[4]设C是实Hilbert空间H的非空闭凸子集。对x∈H，C中存在唯一的PCx，使得‖u-PCx‖=inf{‖u-v‖:v∈C}，称PC:H→C为H到C的最近点投影(或度量投影)。度量投影PC:H→C满足

〈u-PCx,v-PCx〉≥0，∀u∈H，v∈C。

(4)

定义3[5]设C是实Hilbert空间H的非空闭凸子集。算子T：C→H称为是次压缩的，如果存在常量β∈[0，1)使得

‖Tu-v‖2≤‖u-v‖2+β‖u-Tu‖2。

(5)

或者等价于

∀(u-v)∈H×F(T)。

(6)

定义4[6]序列{xn}称为关于给定的非空集Ω是F-单调的，如果对∀x∈Ω，有

‖xn+1-x‖≤‖xn-x‖，∀n≥0成立。

引理1[3]设Ω是H的非空闭凸子集。如果序列{xn}关于Ω是F-单调的，那么我们有下列结论：

(2)序列PΩ(xn)强收敛；

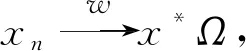
引理2[7]假设{δn}是非负实数序列且满足δn+1≤(1-αn)δn+αnσn，其中{αn}是(0，1)中的序列，{σn}是R中的序列使得

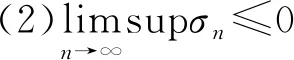
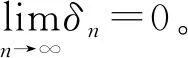
2 主要结果

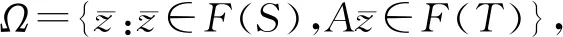
(7)

其中γ∈(0,min{1-β,1-μ})是一常量，τn是由

(8)

证明证明分三步完成。

第1步证序列{xn}有界。

令z=PΩ(f(z))，由(6)和(8)式，我们有

‖xn-z-γτnyn‖2=

‖xn-z‖2-2γτ〈yn,xn-z〉+γ2τn2‖yn‖2≤

‖xn-z‖2-γ(min{1-β,1-μ}-γ)·

‖xn-z‖2。

(9)

下证{xn}有界。事实上，由(7)和(9)可得

‖xn+1-z‖=

‖αnf(xn)+(1-αn)(xn-γτnyn)-z‖≤

αn‖f(xn)-z‖+(1-αn)‖xn-γτnyn-z‖≤

αn‖f(xn)-z‖+(1-αn)‖xn-z‖=

αn‖f(xn)-f(z)+f(z)-z‖+(1-αn)‖xn-z‖

≤αn[η‖xn-z‖+‖f(z)-z‖]+

(1-αn)‖xn-z‖=

[1-(1-η)αn]‖xn-z‖+αn‖f(z)-z‖≤

于是{xn}有界，由于f是压缩映像，故f(xn)也有界。

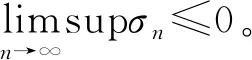
由(7)和(9)可得

‖xn+1-z‖2=

‖αnf(xn)+(1-αn)(xn-γτnyn)-z‖2≤

(1-αn)‖xn-γτnyn-z‖2+

2αn〈f(xn)-z,xn+1-z〉≤

(1-αn)‖xn-z‖2+2αn〈f(xn)-z,xn+1-z〉-

(1-αn)γ(min{1-β,1-μ}-γ)·

(10)

(1-αn)‖xn-z‖2+

(‖xn-Sxn‖2+‖(I-T)Axn‖2)2·

取δn=‖xn-z‖2，

σn=2〈f(xn)-z,xn+1-z〉-

(‖xn-Sxn‖2+‖(I-T)Axn‖2)2·

(‖xn-Sxn+A*(I-T)Axn‖2)-1

(11)

由(10)有

δn+1≤(1-αn)δn+αnσnn≥0。

(12)

由(11)式可得

σn≤2〈f(xn)-z,xn+1-z〉≤

2‖xn+1-z‖(‖xn-z‖+‖f(z)-z‖)，

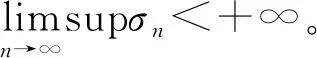
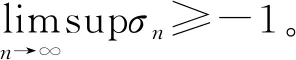
δn+1≤(1-αn)δn-αn≤δn-αn，∀n≥n0。

由归纳法，我们有

(13)

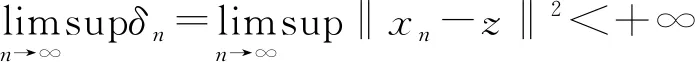
(‖xnk-Sxnk‖2+‖(I-T)Axnk‖2)2·

(‖xnk-Sxnk+A*(I-T)Axnk‖2)-1。

(14)

因为〈f(xnk)-z,xnk+1-z〉是有界实序列，不失一般性。可假设

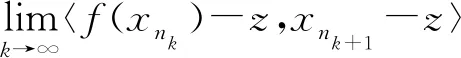
(‖xnk-Sxnk‖2+‖(I-T)Axnk‖2)2·

(‖xnk-Sxnk+A*(I-T)Axnk‖2)-1存在，

因此

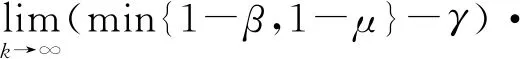
(‖xnk-Sxnk‖2+‖(I-T)Axnk‖2)2·

(‖xnk-Sxnk+A*(I-T)Axnk‖2)-1=0。

(15)

又因为

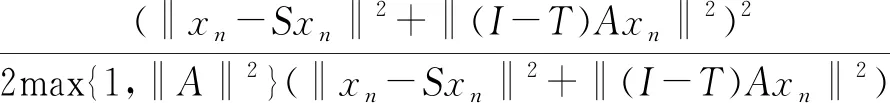
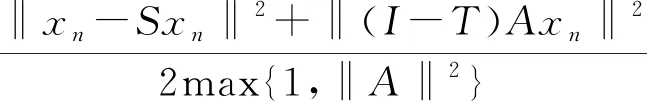
所以由(15)，我们有

(17)

由(15)和(17)可得

因此ωw(xnk)⊂Ω，注意到

‖xn+1-xn‖=

‖αnf(xn)+(1-αn)(xn-γτnyn)-xn‖=

‖αnf(xn)-αnxn-(1-αn)γτnyn‖≤

αn‖xn-f(xn)‖+(1-αn)γτn‖yn‖=

αn‖xn-f(xn)‖+(1-αn)γ·

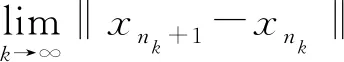
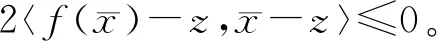
第3步证xn→z(=PΩ(f(z)))。

由于z=PΩ(f(z))且

〈u-PΩ(f(z)),v-PΩ(f(z))〉≥0，

应用引理2.6到(12)，可得

xn→z(=PΩ(f(z)))。证毕。

注1：在算法(7)中令f≡u时，可得到算法(3)，所以定理1推广和改进了文献[3]中的结果。