高压高产气井油管柱特殊螺纹密封动力学研究
2020-07-01练章华林铁军
张 颖, 练章华, 周 谧, 林铁军
(1.四川轻化工大学机械工程学院,四川自贡 643000;2.西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500)
深井、超深井高压高产气井勘探开发过程中,管柱接头气密封性能是一项复杂而又难以解决的问题。接头螺纹是油管柱中最薄弱的环节,螺纹泄漏或断裂是油管柱最普遍的失效形式,90%以上的气井管柱损坏是由于管柱螺纹接头密封完整性被破坏,直接影响气井的开采周期和寿命[1]。国内外学者针对广泛用于深井超深井、高温高压气井等复杂恶劣工况条件下的特殊螺纹接头开展了大量的理论研究和室内评价试验。日本住友金属工业公司最早研发了带有金属对金属密封结构的特殊螺纹接头[2]。Bradley等[3-4]介绍了高温高压酸性气井中特殊螺纹扣气密封的设计和检测方法。王建东等[5]采用有限元分析方法研究了不同密封结构形式下特殊螺纹接头密封能力随载荷的变化规律。许志倩等[6-8]研究了表面粗糙度对非API螺纹密封性能的影响。许红林等[9-10]基于密封接触能机制和密封面屈服条件,建立了特殊螺纹气密封性能定性的评价方法。Ernens等[11-12]开展了特殊螺纹金属对金属气密封性能模拟实验,分析了影响金属气密封性能的因素。目前关于特殊螺纹密封性能的研究大多从弹塑性力学有限元分析出发,考虑特殊螺纹密封面在静力学作用下的密封接触问题[13-18],未考虑振动载荷作用下特殊螺纹密封面接触动力学与气密封性能的关系,没有形成关于高温高压高产气井特殊螺纹密封动力学的完整理论。因此,笔者引入接触动力学理论,根据高产气井高频振动特点,研究特殊螺纹密封面上受动载影响下密封面力学特性,开展密封面结构和油管所受冲击载荷对密封面接触应力影响的敏感性研究。
1 特殊螺纹密封面接触动力学模型
1.1 理论模型
在高产气井中,油管受到高速气流冲击产生颠振,母接头和公接头密封面之间产生相对滑动。以特殊螺纹密封面锥面对球面密封形式为例,特殊螺纹密封面上滑动接触力学模型见图1。螺纹上扣拧紧完成后,螺纹密封面在径向方向限制其自由移动,即图1中y轴方向,同时受高速气流冲击,螺纹接头密封面在水平表面上左右往返运动,并取x轴平行于滑动方向。
由于特殊螺纹接头密封表面的滑动运动,在螺纹密封表面上将会产生一个切向摩擦力Q,该力分别作用在母接头和公接头的密封接触面位置,其方向与运动方向相反,该切向力代表接触表面之间的“动摩擦”力。
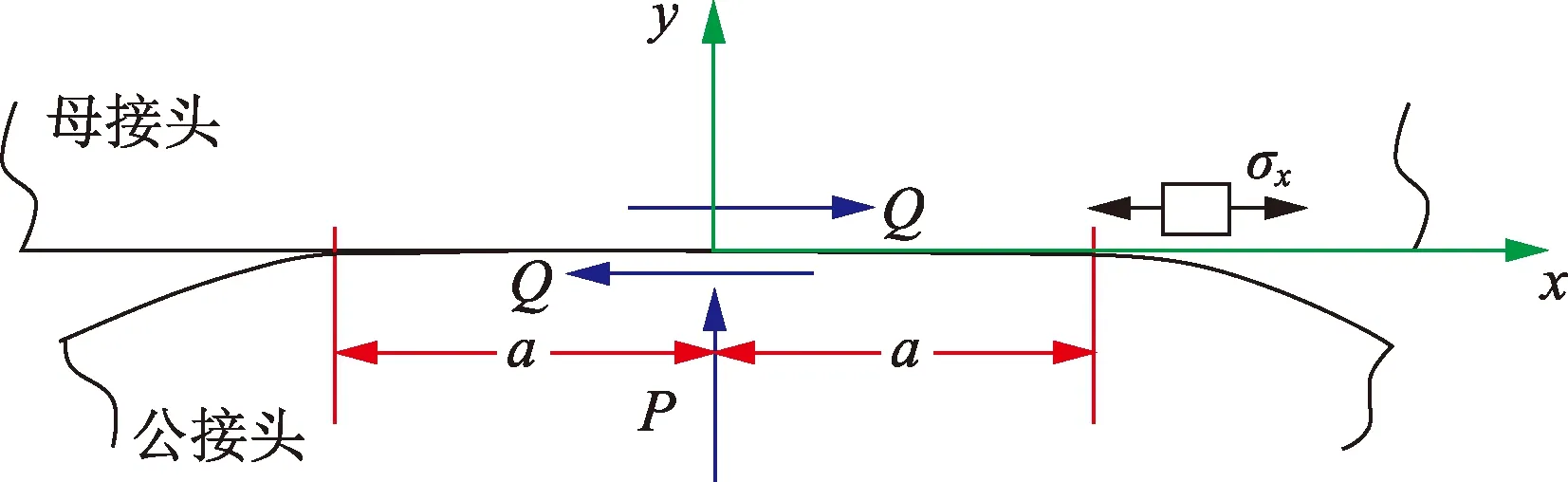
图1 特殊螺纹密封面滑动接触力学模型Fig.1 Mechanical model of premium connection sealing surface sliding contact
为了计算由切向力引起的弹性应力和位移,采用Hertz[19]理论的基本假设,即在接触区附近两个物体都可以被认为是一个弹性半空间体,并且假设由于法向压力和切向力的作用而产生的应力和变形是相互独立的,即接触面的总应力等于其分应力的叠加。
滑动接触中切向力和法向压力之间的关系为
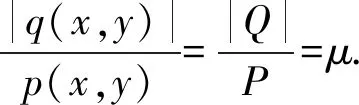
(1)
式中,μ为动摩擦的一个常系数,它是由材料和接触面的物理环境所决定;Q、q(x,y)为切向力,N;P、p(x,y)为接触法向压力,N。
由图1所示,接箍和管体密封面间的接触宽度为2a,根据Hertz理论,其法向压力分布为
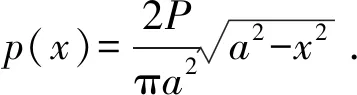
(2)
式中,P为母接头与公接头密封面接触的法向压力,N;p(x)为在x位置处的接触法向力,N;a为接触面接触宽度,mm。
根据式(1)和(2),其接触面上的切向力为
(3)
式中,切向力的正负号与表面运动方向有关,取向右为正;q(x)在接触面x位置处的切向力,N。
在特殊螺纹密封面上的接触应力σx=σy=-p(x)。在接头密封面非接触区域内,表面上的所有应力分量为零。由于正压力在接触区域边缘降为零,其接触区域内最大接触压力为
(4)
式中,E*为螺纹接头弹性模量,MPa;R为特殊螺纹密封面球面半径,mm;pm为接触面平均接触压力,N;p0为接触区域内最大接触压力,N。
沿着载荷作用方向(y轴),其应力分量为
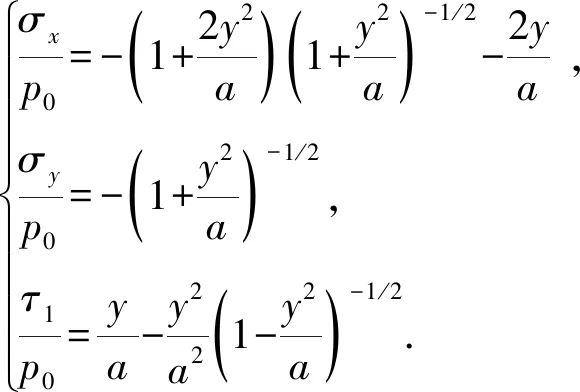
(5)
式中,p0为密封面上的最大接触压力,N;σx和σy分别为x和y方向的应力,MPa;τ1为切向的应力,MPa。
从式(5)可以看出,这些应力分量均与泊松比ν无关。对于平面应变问题,第三主应力的表达式为σz=ν(σx+σy)。
由式(5)可以求出σx、σy和σx在密封面xy平面上的应力分布。平面上主剪应力的计算公式为
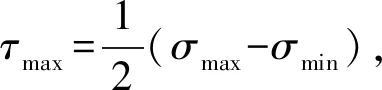
(6)
σz=ν(σx-σy).
(7)
式中,σmax和σmin分别为最大和最小主应力,MPa;σz为z方向应力,MPa。
1.2 接触应力对密封性能影响
假设特殊螺纹公接头密封面球面半径R为100 mm,弹性模量E为207 GPa,泊松比为0.3,密封面上最大接触压力为1 000 N。
Von-Mises应力强度表达式为
(8)
式中,σvon为Von-Mises应力,MPa。
根据式(8)可以绘出特殊螺纹上扣拧紧后,当最大接触压力为1 000 N时,密封接触面下的Von-Mises应力分布见图2(a)。从图2中可以看出,最大的Von-Mises应力为140 MPa,发生在接触面的正下方0.5 mm位置。通过计算,该螺纹密封面接触宽度为2a=1.7 mm。
最大接触压力P0上升至2 000 N时,螺纹密封接触表面下的Von-Mises应力等值线见图2(b)。可以看出,在不同最大接触压力作用下,Von-Mises应力等值线分布相似,但是在Von-Mises应力等值线数值有所不同,表现为密封面上接触压力增加,Von-Mises应力值增大。
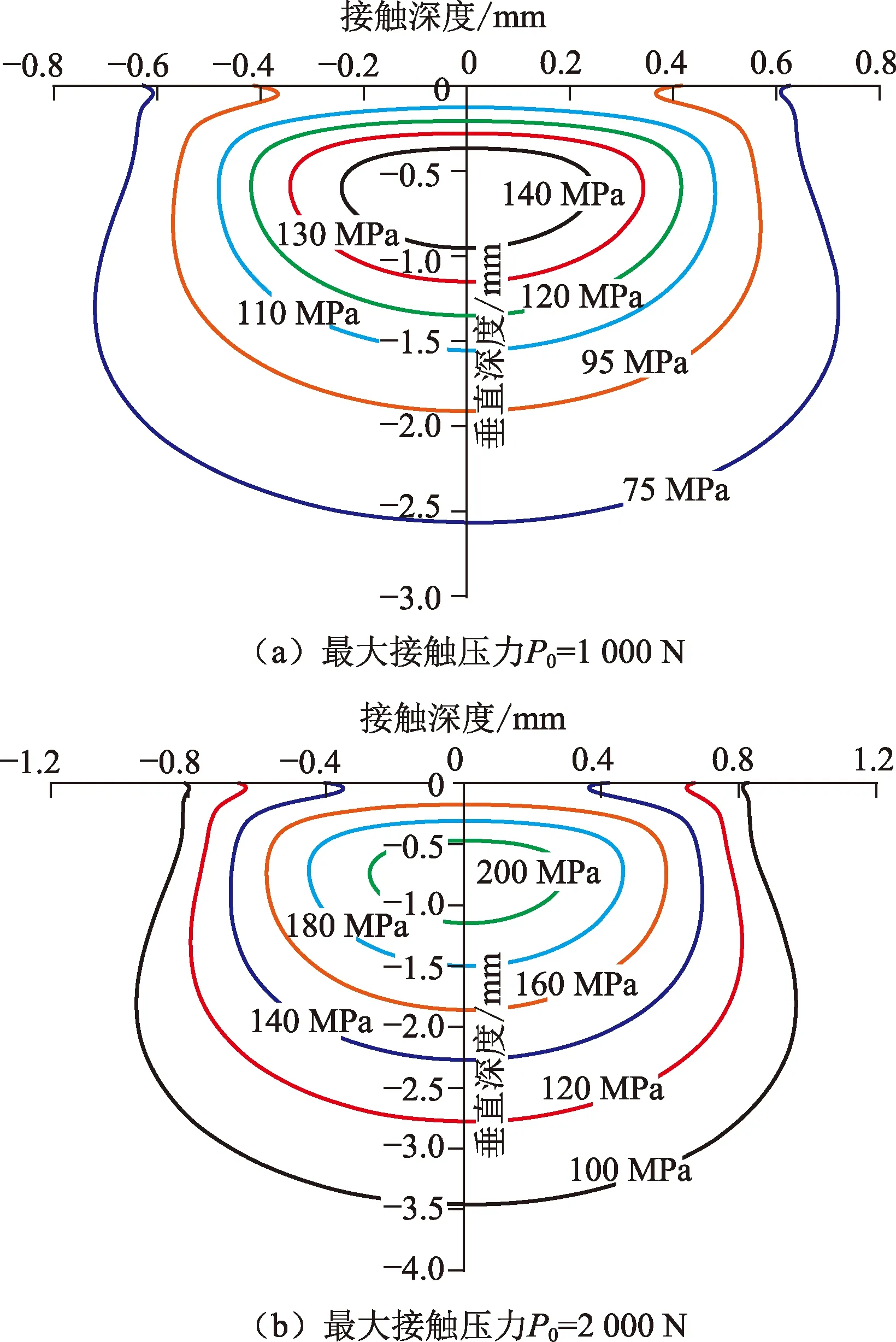
图2 螺纹密封接触表面下的Von-Mises应力等值线Fig.2 Von-Mises stress contour of under premium connection sealing surface
1.3 球面半径对密封性能影响
由于在设计特殊螺纹密封结构时,球面对锥面密封结构设计主要是通过改变球面半径来改善密封面的应力分布。在此,对公接头球面半径对密封面上Von-Mises应力分布的影响进行讨论。假设螺纹材料、结构等参数不变,密封面上最大接触压力为2 000 N,球面半径分别增至150和200 mm,其密封面接触面下的Von-Mises应力分布见图3。从图3中可以看出,球面对锥面的密封形式中球面半径对接触应力的分布大小有显著影响。球面半径越小,接触应力越集中,接触应力也就越大,且接触宽度也越小。
1.4 摩擦系数对密封性能影响
根据Johnson[19]研究计算发现由切向力产生的应力和由法向力产生的应力之间存在某些相似之处,它们可以表示为
(9)
(10)
式中,q0=μp0,是在x=0处的切向力,且下标p和q表示由法向压力和切向力单独作用而产生的应力分量;τxz为xz平面上的切应力。
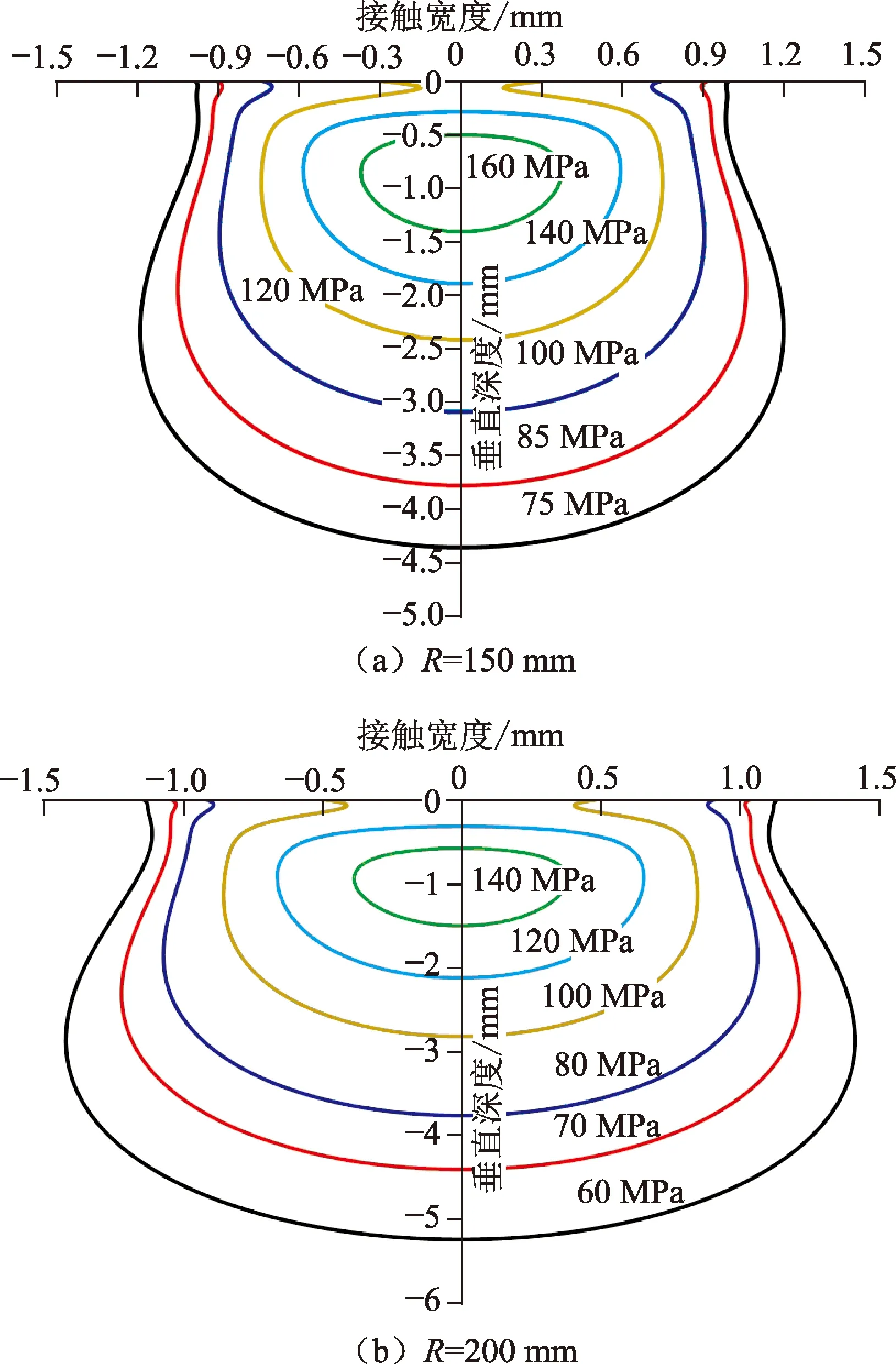
图3 最大接触压力为2 000 N时螺纹密封接触表面下的Von-Mises应力等值线Fig.3 Von-Mises stress contour of under premium connection sealing surface at maximum contact stress of 2 000 N
根据式(5)所给出的关于(τxz)p和(σx)p的表达式,并利用式(9)和(10)可直接求出切向应力所产生的(σz)q和(τxz)q应力分量,表示为
(11)

(12)
其中

但是平行于表面的正应力(σx)q必须单独计算,按照上述表达方法,可以将它表示为

(13)
对于螺纹密封面接触表面,如果接触表面产生相对滑动,假设接触表面运动方向向右,那么作用在滑动平面上的切向力方向向左,而在接触区域的边缘(x=a)处正应力达到一个最大拉应力2q0,在x=-a位置有一个最大压应力-2q0。由于力的相互作用性,在接触区域内法向压力在表面处产生一个相等的压应力(σx)p=-p(x),在接触区域外应力分量为零。因此不管接触表面摩擦系数如何,在滑动接触过程中最大合成拉应力产生在x=a处,其值为2μp0。
根据第四强度理论,在滑动接触中塑形屈服的开始是其应力场中最大Von-Mises应力达到材料屈服强度。当考虑螺纹密封面之间的摩擦系数,即特殊螺纹密封面球面和锥面相互滑动时,利用式(11)~(13),假设接头密封面之间的摩擦系数为0.2,由法向压力和切向力共同作用产生的Von-Mises应力等值线绘在图4中。如图4所示,此时的最大Von-Mises应力发生在靠近表面的接触边缘两侧。
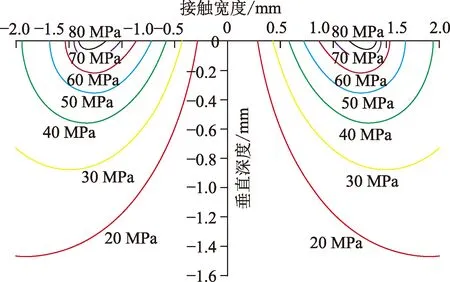
图4 滑动接触下接触面Von-Mises应力等值线Fig.4 Von-Mises stress contour under sealing surface in sliding contact
为了方便计算,以Tresca屈服准则为例,计算密封面开始初始屈服时的接触应力P0,并且假设该最大剪应力等于纯剪切应力k。Tresca屈服准则表达式为

(14)
将(σz)q和(σx)q的表达式代入式(14)中,可得
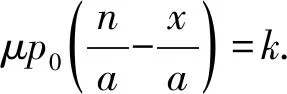
(15)
2 特殊螺纹密封接头受振荡载荷作用的计算
油管在井下受气流颠振,密封面受到振荡载荷Q的作用。振荡力从零开始增加,当振荡力上升到最大值Qm时,此时振荡力开始下降,相当于在切向力中施加一个反方向的增量。当振荡力下降到零之后,振荡力开始沿反方向增加,直至增加到最大值,最后振荡载荷沿正方向减小至零,循环作用。其力学载荷位移循环图见图5。振荡载荷首先沿OA段上升至最大值Qm,此时密封接触面有最大位移δm。然后沿ABC段反方向增大至-Qm,此时对应最大负向位移-δm。最后沿正方向CDA段逐渐上升,完成循环。整个过程类似于加载、卸载、加载的往复循环过程。

图5 振荡载荷与位移关系Fig.5 Relationship between oscillating load and displacement
在一个完整的循环中,切向力(振荡力)所作的功用回线面积表示,如图5所示。且该功被圆环c≤r≤a中微滑方向的倒转所耗散。每一个循环能量耗散的表达式[19-20]为

(16)
式中,ΔW为能量耗散值,J;a为接触表面正应力产生的接触半径,mm;μ为摩擦系数;ν1、ν2为材料的泊松比;G1、G2为材料的剪切模量,MPa。
在反复出现振荡过程中,切向力将会在发生振荡滑动的圆环内产生一些界面磨损。即能量耗散值将会以密封接触面之间的磨损表现出来。
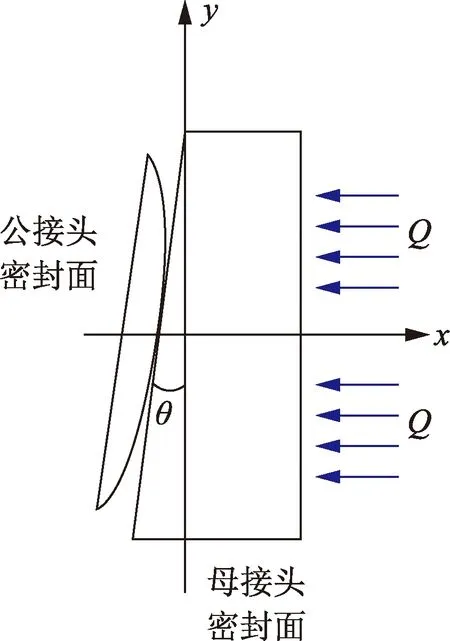
图6 锥面与球面密封接触Fig.6 Sealing contact with conical surface and spherical surface
因此,在考虑密封面锥度时,油管振动过程中接头螺纹密封面上每个循环的能量耗散可表示为
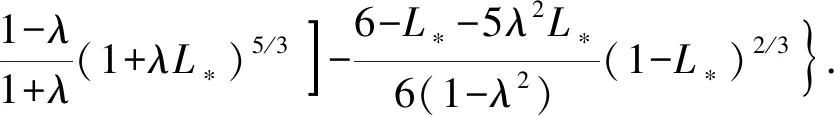
(17)
其中

(18)
式中,θ为为母螺纹密封面的锥角,(°)。
如果振荡力作用方向与母接头密封接触面的切向法向相同,即θ=0,特殊螺纹密封球面与柱面接触即为此种类型的特例。
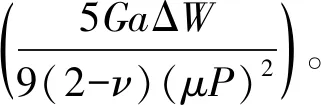
在受到振荡力作用的两个表面之间的接触位置,振荡微滑通常与腐蚀相结合产生特有的表面破坏,称之为“微振磨损”。在高温高压气井中,由于微振磨损的存在,能够导致油管特殊螺纹接头因疲劳而形成过早的破坏或者泄漏。为了尽量避免微振磨损,在特殊螺纹密封面结构设计的过程中,应该尽量减小母接头密封面锥角。其次,应当尽量避免接触区域切向应力的高度集中。即避免接触区域边缘产生“尖锐切口”。也就是说球面对球面、球面对锥面、锥面对锥面3种密封形式中,锥面对锥面最好,其次是球面对锥面,球面对球面最差。
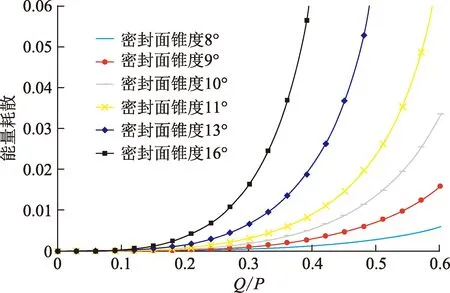
图7 不同密封面锥角下能量耗散对比Fig.7 Comparison of energy dissipation under different cone angle of sealing surface
3 结 论
(1)公接头密封球面半径对接触应力分布有显著影响。公接头密封球面半径越小,接触应力越集中,接触应力也就越大,密封接触宽度也越小。
(2)根据微振磨损与能量耗散呈正关联特性,针对特殊螺纹球面和锥面的接触形式,建立的高产气井特殊螺纹密封面上的能量耗散力学模型,能够分析不同螺纹锥度情况下振荡载荷对油管柱接头能量耗散的影响。
(3)为尽量避免微振磨损,建议合理优化特殊螺纹主密封面锥度,适当减小母接头密封面的锥角设计;特殊螺纹主密封面结构优先采用锥面对锥面密封结构形式,其次采用球面对锥面结构形式。
