联合EMD及小波阈值去噪在电成像测井数据中的应用
2020-07-01徐方慧王祝文刘菁华欧伟明
徐方慧, 王祝文, 刘菁华, 欧伟明
(吉林大学地球探测科学与技术学院,吉林长春 130026)
裂缝性火成岩储层的储集空间主要是裂缝和溶蚀孔洞,利用测井资料对其评价尤为关键[1-2]。电成像测井技术作为一种高分辨测井,能够解决一些常规测井无法解决的问题[3-4],它根据井壁岩层电导率的不同,测量得到一系列分辨率较高的电导率曲线,地层井壁上的裂缝、孔洞均能清晰地反映在电成像测井图上。前人利用成像资料评价储层中裂缝和碎裂带,取得了较好的效果[5-6]。但是在成像测井钻洞过程中,钻头震动会使井壁变得不平整,形成浅的孔洞或划痕,使测量到的电导率数据发生波动,这些低电导率的背景信息在电导率曲线表现为幅值较低的锯齿状,导致电成像静态图上会形成麻点状的噪声和颜色相对较深的条、块状干扰。研究表明[7]钻井液流入会增强裂缝、孔洞边界处的导电性,从而电导率曲线的边界会变宽,当裂缝、溶蚀孔洞比较密集时,边界变宽效应会形成整片的高电导干扰。这些背景噪声不仅影响裂缝的识别,还会降低缝洞参数的准确性以及缝洞参数与常规测井参数、岩心分析数据的相关性,所以有必要消除这些背景噪声。小波阈值去噪方法是在小波分析的基础上发展起来的[8],适用于一些测井数据[9],但是对于属于非平稳信号的电导率数据,小波阈值去噪方法仍存在着一些局限性[10]。此外经验模态分解法(empirical mode decomposition,EMD)[11-12]也是处理非平稳信号的经典方法。应用EMD降噪时只需剔除部分固有模态函数(intrinsic mode function,IMF)即可。但是若剔除的IMF分量包含反应储层特征的有用信号,则会造成信号缺失。前人将EMD和小波变换两种方法相结合来改进小波变换在处理非平稳信号上的不足和EMD降噪方法可能会丢失有用成分的缺点,提出联合EMD及小波阈值去噪方法[13-14],该方法还未应用在电成像测井数据中。电导率数据属于典型的非平稳、非线性信号,适合EMD分解和小波变换。笔者以此为基础,对电导率曲线中部分高频IMF分量进行小波阈值去噪,以压制电成像测井图中的背景噪声;利用统一阈值分割电成像静态图像并输出仅保留裂缝和溶蚀孔洞的灰度子图像,利用该子图像计算缝洞面孔率,与实际岩心分析孔隙度、常规测井资料孔隙度以及人工提取的裂缝面孔率对比,验证对电导率数据去噪的必要性以及提取的缝洞信息的有效性和合理性。
1 EMD去噪方法的原理
对任意的原始电导率信号x(t)进行EMD[11-12]分解得到下式:
(1)
式中,j为分解次数;cj(t)为第j个IMF分量;rn(t)为原始电导率信号x(t)的趋势分量。由于信号EMD分解得到的基函数cj(t)具有自适应性,故EMD方法适合处理类似于测井阵列声波信号和电导率信号等非平稳信号。
实际误差S计算公式为
(2)
其中hn(t)为原始电导率信号减去上下包络均值mn(t)得到的新信号,一般实际误差需要满足:0.2≤S≤0.3。
需要从以下两点判断固有模态函数的有效性[15]:
(1)cj(t)局部数据的零点与极值点的数量差a需要满足|a|≤1。
(2)在cj(t)每个时间点上,局部数据上下包络均值需为0。
对任意IMF分量cj(t)进行希尔伯特-黄变换[11-12](简称HHT)可得到瞬时振幅和瞬时频率,如果把振幅显示在频率-时间平面上,就可以得到IMF分量cj(t)的HHT幅值谱Hj(ω,t),把所有IMF分量的HHT幅值谱Hj(ω,t)叠加就得到了整个电导率信号的HHT幅值谱H(ω,t),将H(ω,t)对时间积分得到电导率信号的HHT边际谱,HHT边际谱能直观地展现信号的频率分布情况。
信号EMD分解后,各IMF分量按频率高低排列,由此发展了EMD去噪方法:若去掉若干个高频IMF分量再与其余分量重构信号得到x1(t),则相当于低通滤波;若去掉若干个低频IMF分量再与其余分量重构信号得到x2(t),即相当于高通滤波;若同时去掉若干个高频和低频IMF分量再以其余分量重构信号得到x3(t),即为带通滤波。
低通滤波可表示为
(3)
高通滤波可表示为
(4)
带通滤波可表示为
(5)
式中,b、k为IMF分量的阶数。
通过EMD去噪方法的3种滤波方式可知,若噪声存在于信号的低频或高频部分,利用EMD低通或高通滤波便能有效压制噪声;若噪声的频率范围覆盖了整个信号,信号EMD分解后噪声也随之分布于每个IMF分量中,直接剔除若干IMF分量则会丢失有用信号,破坏信号的完整性。故EMD去噪方法更适用于噪声分布较有规律的非平稳信号。
2 小波阈值去噪方法
小波阈值去噪是在小波变换[16-18]的基础发展起来的,首先对原始电导率信号x(t)进行小波分解得到小波系数;然后对其进行相应的数学处理;最后信号重构。其中阈值函数、阈值估计方法和小波基函数的类型都会对原始信号的去噪质量产生一定影响。阈值函数主要分为2种,即硬阈值和软阈值函数。设ω是原始电导率信号x(t)分解得到的某小波系数,λ是估计的阈值,ωλ是阈值处理后的小波系数。那么硬阈值函数可以表达为

(6)
软阈值函数可表达为

(7)
由式(7)看出软阈值函数得到的重构信号与原始小波系数存在恒定偏差。
阈值λ的确定同样重要。常见的阈值估计方法包括4种:Stein无偏似然估计阈值(rigrsure阈值)、固定阈值(sqtwolog阈值)、heursure阈值(启发式 SURE 阈值)和极大极小阈值(minimax阈值)[19](本文中阈值估计方法均使用英文简称)。
2.1 Stein无偏似然估计阈值
设X为某小波系数,Q=[Q1,Q2,…,Qn],并且Q1≤Q2≤…≤QN,N为小波系数X的长度,Q是小波系数X的平方由小到大排列得到的。通过向量Q可得到风险向量R=[R1,R2,…,RN],其元素为
(8)
找到R中的最小值Ri,由Ri下角标的数字i确定阈值λ为
(9)
式中,σ为噪声信号标准差。
2.2 固定阈值
sqtwolog阈值公式为
(10)
2.3 启发式 SURE 阈值
heursure阈值是Stein无偏似然估计阈值和固定阈值的综合。若信号的信噪比小且rigrsure阈值误差较大,可采用sqtwolog阈值;若信噪比大且sqtwolog阈值去噪的效果不佳,从两种方法中选取较小者作为阈值。
2.4 极大极小阈值
极大极小原理最初在应用在统计学中。minimax阈值计算公式为
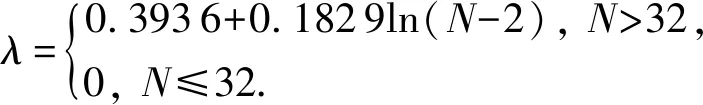
(11)
3 基于EMD的小波阈值去噪方法
为了确定电成像测井数据中的背景噪声范围,图1给出了一条典型电导率曲线的HHT边际谱[20]。通过HHT边际谱发现电导率信号中高电导信息主要存在于小于3 kHz的低频区域,低电导率信息存在于高频部分。由于裂缝和溶蚀孔洞在地层中径向深度较大,被井中钻井液侵入后电导率会明显增大,在电导率曲线中,相对于基岩,裂缝和溶蚀孔洞电导率很高、幅值很大。钻头震动会在井壁上形成浅的孔洞和划痕,由于钻井液侵入的原因其电导率也会比基岩大,但相对于裂缝和溶蚀孔洞来说,背景噪声的电导率要小得多,幅值较低[21],具体表现在电导率曲线上为幅值较低的锯齿状波动,并且在电成像测井图像上背景噪声一般比较密集。综合认为电导率曲线中的背景噪声主要为高频的低电导部分,并以此为前提对电导率曲线进行去噪。
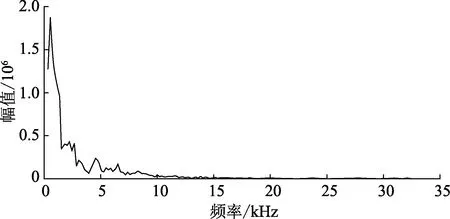
图1 电导率曲线的HHT边际谱Fig.1 HHT marginal spectrum of conductivity curve
电导率曲线进行EMD分解后得到了若干IMF分量(图2),舍弃部分高频率的IMF分量在一定程度上能够减少噪声和干扰。图2中signal为原始电导率信号;EMD1曲线是原始电导率信号舍弃IMF1和IMF2分量的结果,压制噪声的效果并不明显;EMD2曲线表示电导率信号舍弃IMF1、IMF2和IMF3分量的结果,有一定的降噪效果,同时弱化了一些高电导率波峰的幅值;EMD3曲线表示电导率信号舍弃IMF1、IMF2、IMF3和IMF4分量的结果,降噪效果好,但是丢失信息严重。这是因为有些高频IMF分量中不仅存在着背景噪声,同时还包含了不可直接忽略的信息,将其舍弃则会使电成像图丢失部分细节和特征。

图2 电导率曲线的EMD去噪处理结果及其各IMF分量Fig.2 EMD de-noising of conductivity curve and its IMF components
为了测试小波阈值去噪方法的效果,笔者尝试了rigrsure、sqtwolog、heursure和minimax 4种阈值估计方法,选择了硬阈值函数处理电导率曲线(小波基函数选择sym5),阈值根据每层小波系数的特征进行调整。如图3,signal是电导率曲线;rigrsure、sqtwolog、heursure和minimax是小波阈值估计方法;-h(s)表示硬(软)阈值函数。从图3可看出当选择硬阈值函数时,除了rigrsure阈值,其他3种阈值都能明显压制噪声,但曲线畸变明显。
综上,若单一地将电导率曲线进行小波阈值去噪或者EMD去噪,虽然能去除部分背景噪声,但是会使信号丢失、畸变。为了解决这一问题,考虑应用联合EMD及小波阈值去噪的方法对信号去噪。由于背景噪声主要存在于电导率曲线的高频部分,因此只需对高频IMF分量进行小波阈值去噪,再与其余IMF分量叠加,这样既完成了信号的降噪工作,也能较好保证信号的完整性。
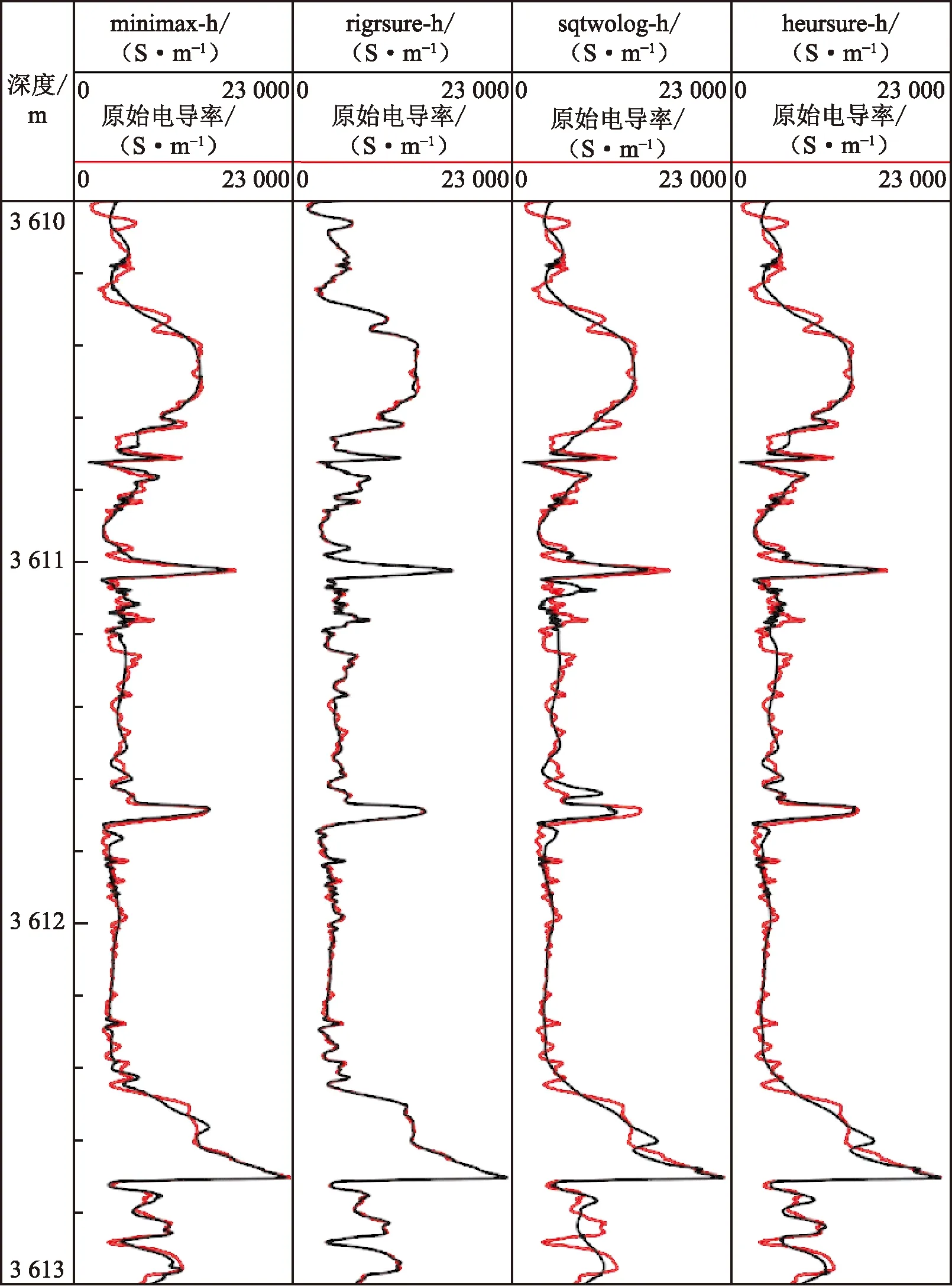
图3 电导率曲线的4种小波阈值去噪结果Fig.3 Four wavelet threshold de-noising results of conductivity curve
图2中将各IMF分量与原始电导率曲线对比,发现噪声主要存在于分量IMF1、IMF2、IMF3和IMF4中。其中IMF1是电导率曲线中频率最高的分量,且幅值很低,主要是一些无用的背景噪声,本文中将其忽略。随着频率的降低,IMF2、IMF3和IMF4中的背景噪声成分逐渐减少。故对IMF2、IMF3和IMF4分量进行小波阈值去噪。
IMF2分量属于电导率曲线中频率较高的成分,包含大量背景噪声。观察图4发现,minimax、rigrsure、sqtwolog和heursure 4种阈值估计方法中,软阈值函数的缺点是会削弱电导率信号的一些峰值,但压制背景噪声的效果更好。由于IMF2的幅值相对原始信号要小得多,所以幅值略微降低对电导率曲线的整体影响不大,故选择软阈值函数来处理IMF2分量。从图4能看出,rigrsure-s的降噪效果最差,sqtwolog-s平滑噪声效果最好,故IMF2分量最终选用sqtwolog软阈值函数去噪。

图4 IMF2分量的小波阈值去噪结果Fig.4 Wavelet threshold de-noising of IMF2 components
同理对IMF3、IMF4分量去噪。IMF3、IMF4分量的频率降低,幅值较大,包含大量有用的高电导率成分,若削弱高电导率成分对电导率曲线影响较大,所以选择软阈值函数是不合适的,故选取能较完整保留信号特性的硬阈值函数。通过实验和参考前人的成果发现[8-10]:rigrsure硬阈值去噪效果较差,其他3种硬阈值函数对噪声都有较好的压制效果,综合上述结果,笔者选择了minimax硬阈值函数处理IMF3和IMF4分量。
将其余IMF分量与去噪的IMF2、IMF3和IMF4分量叠加,得到图5去噪的电导率曲线sym5(蓝色曲线)。与小波阈值去噪、EMD去噪的电导率曲线相比,曲线sym5未产生明显畸变,并且减少了背景噪声,还较完整得保留了高电导信号。
4 方法应用
按照上述方法对辽河东部和冀东地区裂缝性火成岩地层Y井、X井某井段的150(192)条电导率曲线进行处理,软件绘制成电成像静态图。如图6所示,去噪后电成像静态图中麻点状噪声和块状干扰明显减少,裂缝特征更加清晰、明显,有利于人工拾取裂缝。
为了验证以上方法的必要性和有效性,设置统一阈值分割去噪前、后的电成像测井图,输出仅包括裂缝、溶蚀孔洞的灰度图来计算地层的缝洞面孔率[22]。有研究指出根据电成像数据得到的缝洞面孔率与常规资料得到的裂缝孔隙度之间可能存在较大差别,但二者明显线性相关[23-24],故常规资料孔隙度一定程度上能反应缝洞面孔率的合理性。地层的缝洞面孔率可定义为单位井壁上裂缝和溶蚀孔洞所占的比例。计算地层的缝洞面孔率ps[22]:
(12)
式中,Qt为单位电成像灰度图总的像素点个数;q为单位电成像灰度图裂缝、溶蚀孔洞所占的像素点个数。

图5 电导率曲线基于EMD的小波阈值去噪、小波阈值去噪和EMD去噪对比Fig.5 Comparison of wavelet threshold de-noising based on EMD, wavelet threshold de-noising and EMD de-noising of conductivity curve

图8(a)中井径曲线显示井况较好。原始图像分割结果麻点状噪声和干扰明显,计算的原始缝洞面孔率较大且没有明显规律;去噪图像分割结果背景噪声减少,特征清晰,特别地,绿色方框中的去噪缝洞面孔率明显降低,更加符合实际情况。图8中的裂缝面孔率是通过人工拾取裂缝由专门的软件计算得到的。将通过去噪电成像静态图提取的缝洞面孔率与常规测井孔隙度、裂缝面孔率对比发现,经过联合EMD及小波阈值去噪方法处理的电成像测井图计算的缝洞面孔率与裂缝面孔率、常规测井资料中的孔隙度有明显线性关系,对应较好。
为了验证缝洞面孔率的正确性和去噪方法的有效性,计算去噪前、后冀东X井某层段电成像测井图的缝洞面孔率,与实际岩心分析孔隙度为做出交会图(图9)。去噪后的缝洞面孔率与岩心分析孔隙度的相关系数R2为0.339,说明二者线性相关性更强,趋势线可靠性更高,说明联合EMD及小波阈值去噪能够有效降低背景噪声,提高缝洞面孔率的合理性。

图6 电成像静态图去噪前、后对比Fig.6 Comparison of static image of electric imaging before and after de-noising

图7 Y井单位电成像灰度图Fig.7 Gray-scale image of unit electrical imaging of Y well
EMD分解适合非线性、非平稳信号,但存在模态混叠现象。小波阈值去噪中硬阈值函数重构所得的信号会产生伪吉布斯效应,而软阈值方法估计后的小波系数和原始小波系数总存在恒定偏差。由于联合EMD及小波阈值去噪算法本身的原因以及实际信号的复杂性,同时为了尽可能压制噪声选择软阈值方法处理IMF2分量,部分裂缝和溶蚀孔洞对应的正弦信号也被削弱了。故去噪过程中需充分考虑降噪效果以及真实信号的完整性,下一步工作将研究如何在消除背景噪声的同时尽量保证有用信号的完整,利用改进的EMD算法减弱模态混叠效应以及改进小波阈值函数都是一种可尝试的思路。
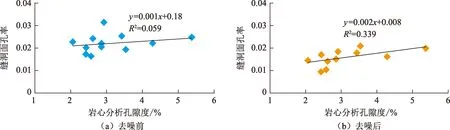
图9 去噪前和去噪后缝洞面孔率与岩心孔隙度交会图Fig.9 Cross plot of fracture-vug plane porosity and core porosity before de-noising and after de-noising
5 结 论
(1)消除了背景噪声的电成像静态图裂缝、溶蚀孔洞的特征更加明显清晰,便于划分和识别。
(2)经去噪的电成像静态图计算的缝洞面孔率与常规资料孔隙度及人工拾取的裂缝面孔率有明显的对应关系,规律明显。
(3)去噪后缝洞面孔率与实际岩心分析孔隙度线性相关性更好,说明联合EMD及小波阈值去噪能提高缝洞面孔率的准确性。
