基于最大相关熵准则的压缩感知地震道重建方法

焦叙明, 杜启振, 赵 强

(1.中海油服物探事业部物探研究院,天津 300000;2.中国石油大学(华东)深层油气重点实验室,山东青岛 266580;3.青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛 266237;4.中国石油大学(华东)CNPC物探重点实验室,山东青岛 266580)

在实际地震资料采集过程中,受野外采集环境以及检波器本身等因素的影响,接收到的地震数据往往存在缺道、坏道等问题。地震道的缺失导致地震信号空间采样的不完备,但常规地震资料处理往往基于信号完备的基本假设。缺失的信息作为干扰源,影响到多次波压制、偏移成像以及道集分析等后续地震资料处理[1-7]。重建缺失地震数据的方法可大致划分为3类:波动方程法、预测滤波法以及信号变换法。波动方程法通过先验的速度场等信息,对地震道缺失位置进行补全。但波动方程法往往会引入巨大的计算量,同时先验速度场信息的准确性也会极大地影响重建地震道的精度。预测滤波法利用相邻地震道的相似性以及可预测性,通过构建合适的预测因子,以现有的地震道为输入,对相邻的缺失地震道进行预测重建,但其预测精度往往取决于预测因子的准确性以及相邻地震道的相似性。信号变换法以数学变换作为基本手段,以变换域中信号的稀疏性以及缺道干扰的非稀疏性作为前提条件,对缺失信息进行重建。针对如何利用信号稀疏性进行地震缺失信息重建的问题,国内外学者进行了大量的研究[8-12]。常规的信号变换法通常利用L2范数作为残差度量准则,可较稳定地处理有随机噪声干扰的重建问题[13]。实际资料中广泛分布的异常振幅噪声往往不满足L2范数所需要的正态分布,这会严重影响该类算法的性能,进而影响地震道重建效果。一般来说,提高传统信号变换法的手段主要有两类:合适的异常振幅噪声检测方法[14-16]以及鲁棒的度量标准[17-18]。现阶段基于鲁棒度量标准的算法普遍需要求取噪声的方差作为输入,利用中位绝对离差通常可在异常振幅噪声存在的情况下对噪声方差进行大致的估计。然而在实际资料处理过程中,噪声情况往往是未知的,这对中位绝对离差的估计造成了一定的不确定性。Liu等[19]通过引入高斯核函数对残差进行度量,提出了最大相关熵准则(maximum correntropy criterion, MCC)。最大相关熵准则以误差的局部相关熵的最大化作为目标函数,利用高斯核函数对预测值与观测值的误差进行正态化约束,使残差结果趋向于零均值,有效地限制了异常振幅噪声对于有效信号估计的影响。基于这种相关熵准则的相关算法,在异常振幅噪声影响下仍可表现出较好的性能[18-20]。笔者从含异常振幅噪声的缺失地震道重建问题出发,引入相关熵,构建以最大相关熵为目标函数的鲁棒地震道重建模型。

1 基于压缩感知理论的含噪缺失地震道重建

不同于香农采样定理,压缩感知重建所需的样本数不由信号本身的带宽决定,而是由信号的稀疏结构及其采样方式的有限等距性质决定[22]。在地震勘探过程中,受地理环境等因素的影响,容易出现不规则的地震道缺失、坏道的问题。不规则的地震道缺失保证了压缩感知理论应用于地震道恢复的可能性。除此之外,野外采集信号往往受各种噪声的干扰。干扰噪声一般可分为两种:相干噪声以及非相干噪声。相干噪声指代面波、多次波等波形噪声,非相干噪声指代随机噪声以及奇异振幅噪声等非波形噪声。考虑到地震道缺失以及非相干噪声的影响,地震资料采集可表示为

y=RΩ(x+n+e).

(1)

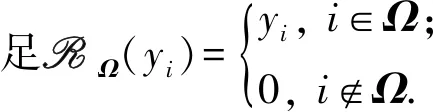
基于压缩感知理论的信号x的恢复过程可表述为求解其最稀疏解α,即

(2)

(3)

式(3)所表示的最优化问题可利用迭代阈值算法[22]进行求解

ak+1=Tλ(ak+ΦT(y-RΩΦak)),

(4)

其中

Tλ(a)=sign(a)max(0,|a|-λ).

式中,ΦT为逆稀疏变换基;ak和ak+1分别为第k、k+1次迭代的稀疏表示结果;λ为迭代过程的阈值;sign(a)表示取α的正负号。

理想情况下,

φ(ri)=ri.

(5)

式中,ri为恢复结果相对于观测结果的残差。式(5)中的敏感度指示了对应的残差在L2范数度量中的影响程度。图1(a)为不同残差ri所对应的L2范数度量值曲线,图1(b)为不同ri所对应的导数值。可以看出,L2范数的导数随差值的增加而递增,说明L2范数的敏感度也随着差值的增大而更加明显。利用随机生成1 000个分布于[-10,10]之间的零均值正态分布数据,并额外添加10个相同的异常值,得到的不同异常值对原始零均值正态分布数据的影响如图1(c)所示。由于L2范数不是鲁棒型的估计,它的代价函数是基于最小均方误差准则的,其统计量可无限增加,观测结果中较大的异常值的影响在L2范数估计中是不受限的,所造成的影响将会被放大。另一方面,如图1(c)所示,均值的估计误差受异常值的影响明显,呈线性增加的趋势,即异常值数值越大,均值的估计偏差越大。对于式(3)而言,其求解过程是一个高度非线性的过程,异常值对最终求解结果的影响程度将会更大。当异常值较大或者较多时,会使算法性能退化,甚至出现不收敛的情况。

图1 L2范数分布示意图Fig.1 Distribution of L2 norm

2 基于最大相关熵准则的压缩感知地震道重建

2.1 非线性相关熵度量准则

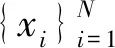
(6)

式中,κσ为带宽为σ的核函数;N为样本总数。高斯核函数可以有效地将低维数据映射到高维空间[18],适合描述从低维采样到高维数据恢复的过程。考虑高斯核函数,式(6)变为

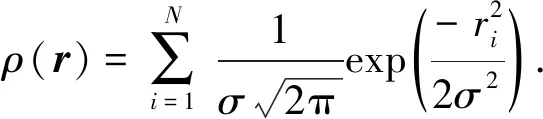
(7)

其中ri=yi-xi为恢复残差。

令N=1,可以通过以下导数来评估式(6)对于不同残差值ri的敏感度:

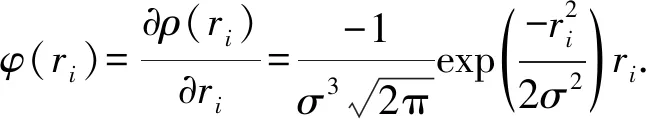
(8)

图2为不同带宽(w)所对应的相关熵以及相关熵敏感度随残差值的变化趋势,可以看出,相关熵具有远端衰减的作用。对比图1与图2可以看出,异常值在L2范数计算过程中起重要作用,敏感度更高,而在相关熵计算中由于远端衰减的作用,其影响可得到一定程度的衰减。不同的带宽对应的相关熵及其敏感度曲线的作用范围不同:带宽越小,相关熵的有效计算范围越小,其导数收敛趋向于零的速度越快,远端异常值的衰减越明显。对于高斯核函数,Liu等[19]指出合适的带宽取值范围为[0.8,3],并且在取值为1时,固有误差达到最小。本文中将带宽固定为1。

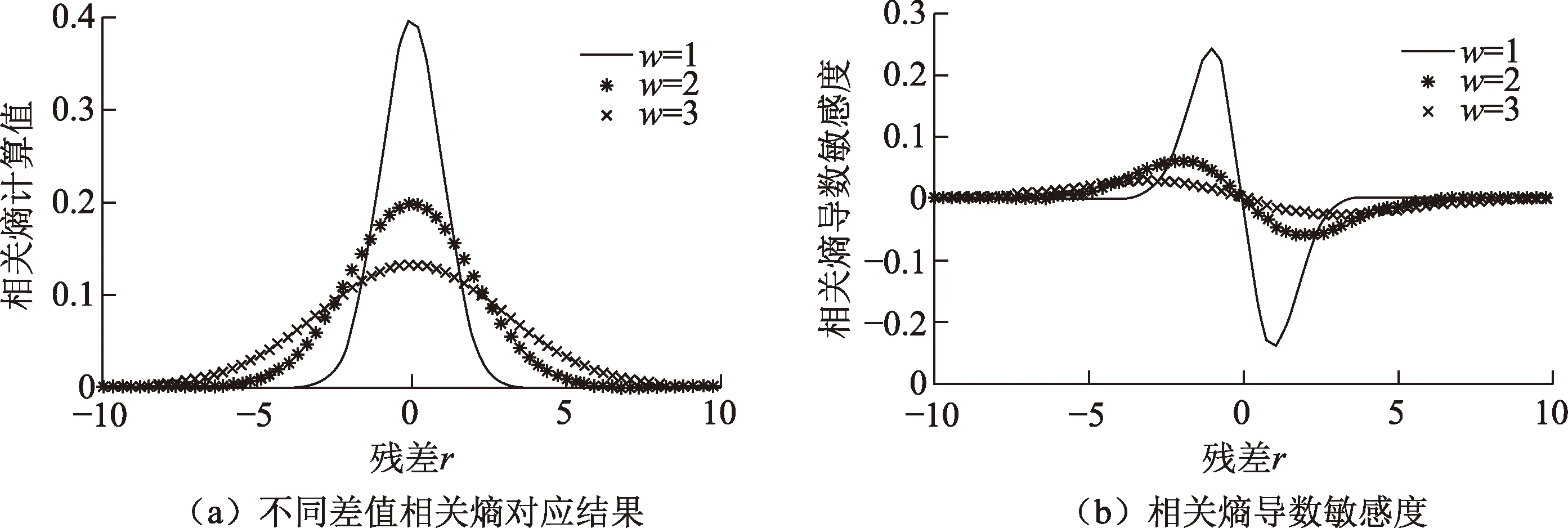
图2 相关熵分布示意图Fig.2 Distribution of correntropy

2.2 基于最大相关熵准则的压缩感知地震道重建模型

在信息论中, 相关熵准则可用来处理受到噪声影响的信号分析[19-21]。在最大相关熵准则下,可以通过最大化观测值和恢复信号之间差值的相关熵来估量恢复结果。从图2(a)可以看出,相关熵函数随着带宽σ的变化存在尺度问题,为此对其进行尺度归一化处理。当带宽σ=1时,归一化后的最大相关熵JM(r)可以表示为

(9)

其中

r=y-RΩ(Φα).

常规的L1范数是求解问题的凸最优化极小值问题。对于严格凸优化问题来说,局部最优解就是全局最优解。从相关熵的表达式及其示意图(图2(a))可以看出,相关熵是明显的凹函数优化问题,难以直接利用凸函数优化算法进行求解。另一方面,同L2范数一样,相关熵函数同样满足极值的唯一性,区别在于L2范数求取极小值,而相关熵函数求解极大值。一个简单直接的解决方案是对常规的相关熵函数乘以-1,便得到以相关熵为度量函数的凸函数极小值优化目标函数JCM(r)为

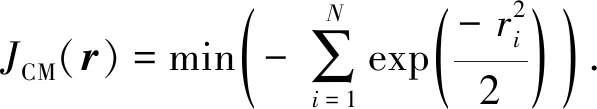
(10)

式(10)本质上等价于求解最大化相关熵,因此仍将式(10)称为最大化相关熵。结合式(10)与式(3),可以得到基于最大化相关熵准则的地震道重建模型

(11)

2.3 基于伪观测数据的迭代阈值求解算法

虽然式(11)是一个凸优化问题,然而相关熵度量标准中指数函数的存在导致其求解过程更加复杂。为此,借鉴Zhao等[18]在解决非线性Huber函数计算时所引入的伪观测数据的构建方式,构造如下第k次迭代时的伪观测数据yP(αk):

yP(αk)=RΩΦαk-φ(y-RΩΦαk).

(12)

将相关熵的梯度表达式代入式(12)中,整理得到

yP(αk)=RΩΦαk+μ(y-RΩΦαk).

(13)

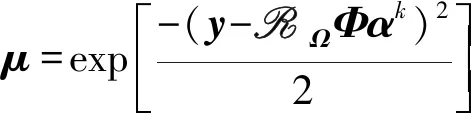
对于式(3)所表示的常规压缩感知恢复模型,第k次迭代时关于残差r的梯度为

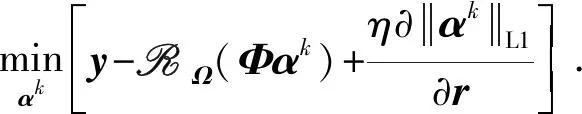
(14)

将伪观测数据yP替换式(13)中观测数据y,并将式(8)表达式代入,得到

(15)

另外,基于最大化相关熵准则的地震道重建模型在第k次迭代时关于残差r的梯度为

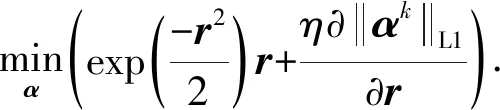
(16)

比较式(15)及式(16)可以看出,当基于L2范数的常规压缩感知模型的输入数据为伪观测数据时,其关于残差的更新梯度等价于基于最大化相关熵准则的地震道重建模型的梯度。利用伪观测数据,基于最大化相关熵准则的地震道重建模型便可以借鉴式(4)的迭代阈值算法进行求解,具体形式为

(17)

3 实验与方法对比

利用如图3(a)所示的模拟地震数据进行测试分析。该模型数据由有限差分方法对SEG/EAGE盐丘模型进行正演模拟得到。正演模拟子波为主频30 Hz的雷克子波,空间及时间采样步长分别为10 m和1 ms。为验证所研究方法的重建效果,首先随机地对地震记录中40%地震道进行充零,模拟地震道缺失的问题;其次,对剩余的地震道添加随机噪声,并对20%的剩余地震道添加异常振幅噪声,结果如图3(b)所示。基于L2范数以及最大相关熵准则的重建结果如图3(c)、(d)所示,去除的噪声剖面如图3(e)、(f)所示。图4为图3(a)～(d)所对应的f-k谱图。对比两种残差度量的重建结果可以看出,基于L2范数的重建结果中缺失地震道基本得到恢复,但重建结果受所添加异常振幅噪声的影响明显,存在局部振幅异常的现象,且去除的噪声剖面中存在明显的有效信号泄漏,频谱图中因噪声及缺失道所引起的干扰去除不完全;基于最大相关熵准则的重建模型对所添加的异常振幅噪声具有更好的鲁棒性,重建结果的信噪比更高,去除的噪声剖面中有效信号相对更少。

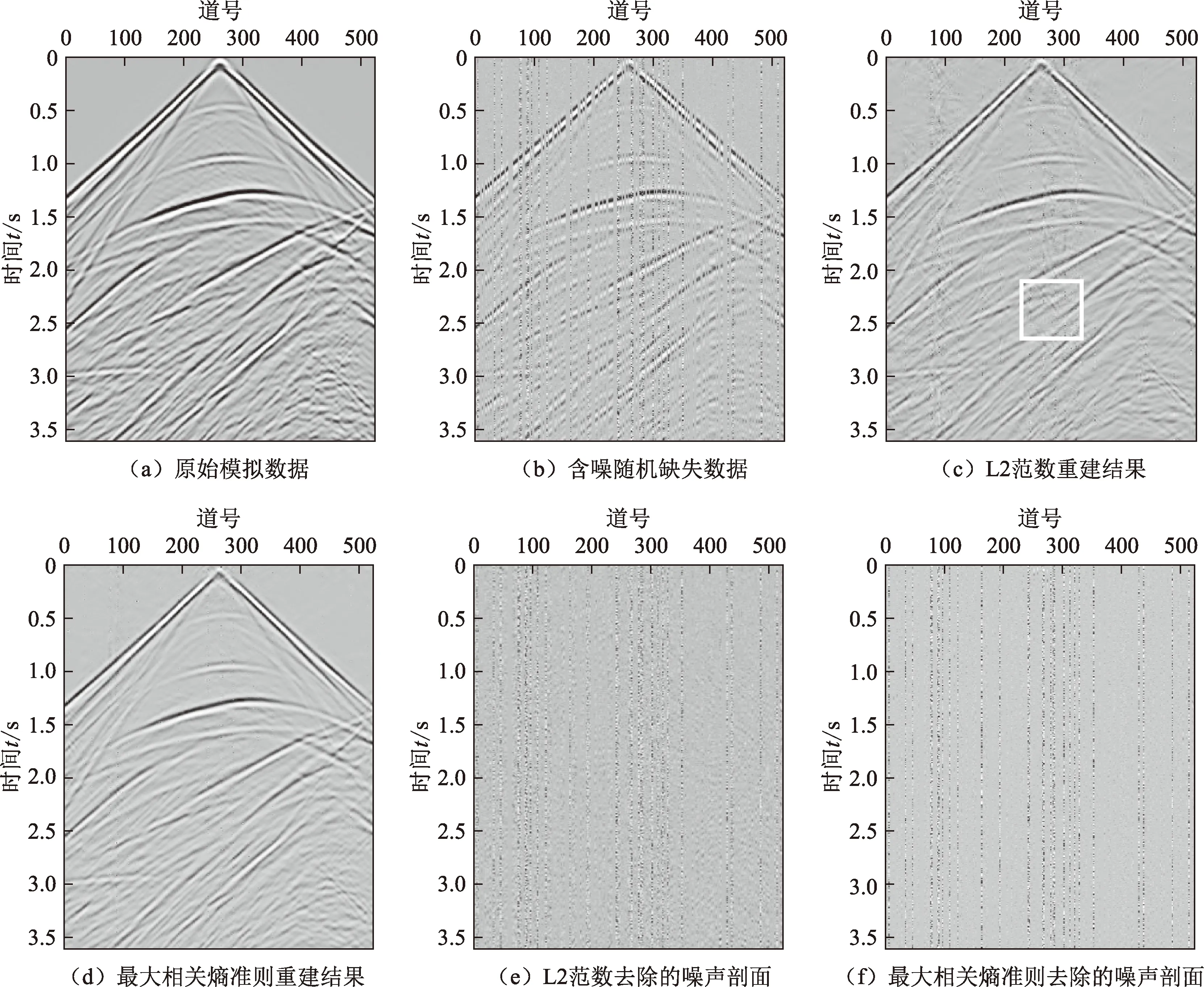
图3 模拟地震数据测试分析Fig.3 Test and analysis of simulated seismic data

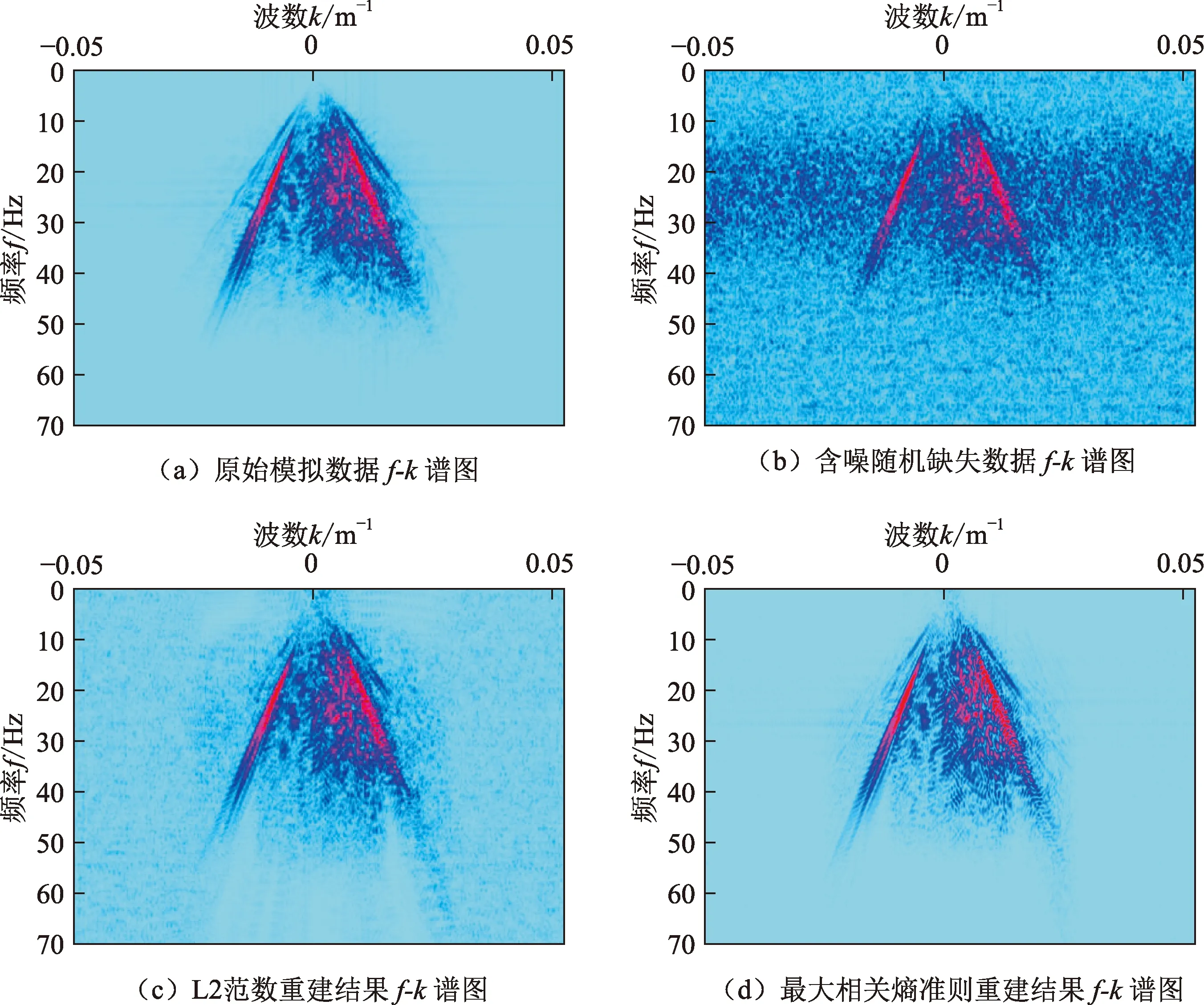
图4 模拟地震数据f-k谱图Fig.4 The f-k spectrum of simulated seismic data

为了进一步验证在不同噪声含量及不同地震道缺失情况下的重建效果,分别固定噪声含量或地震道缺失量,测试两种方法的重构质量及收敛速度。测试结果如图5所示,其中图5(a)为固定地震道缺失比、不同异常噪声含量的重构质量及收敛速度对比结果,图5(b)为固定异常噪声含量、不同地震道缺失的重构质量及收敛速度对比结果。可以看出,随着噪声含量与缺失道的增加,两种方法均能逐渐收敛,验证了压缩感知模型在随机缺失地震道重建中的有效性。在初始迭代环节,L2范数的收敛速度要快于最大相关熵准则,这是因为最开始残差中存在大量有效信号,高斯核函数除了对异常振幅噪声具有压制作用外,还间接地导致了有效信号能量的损失;随着迭代次数的增加,残差中的有效信号逐渐减少,高斯核对于有效信号的影响逐渐降低,而异常振幅噪声仍可得到有效压制。虽然最大相关熵准则的初始收敛速度要慢于L2范数,但在一定的迭代次数后,本文方法的重构质量要明显高于L2范数。

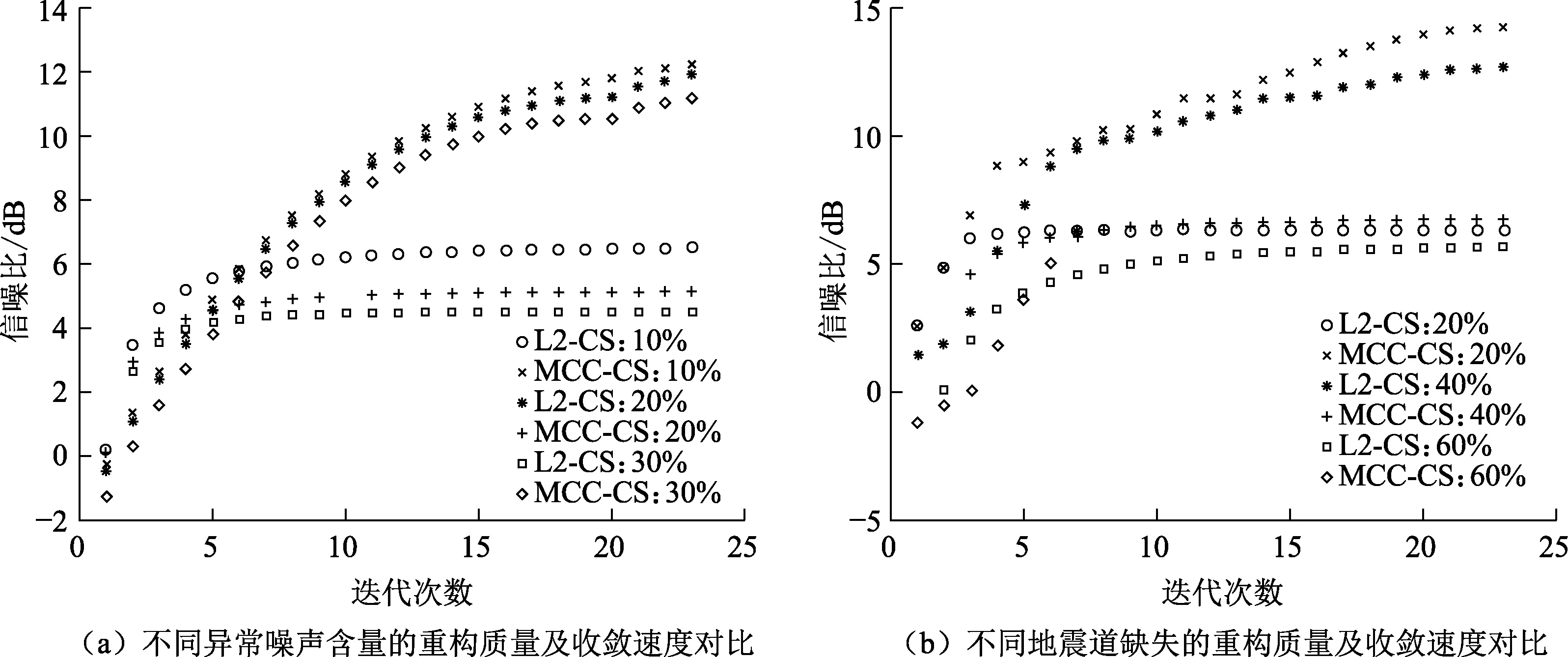
图5 高密集的噪声以及欠采样恢复收敛曲线Fig.5 Recovery convergence curve of high-density noise and under-sampling input

图6为利用本文方法对本测试环节的最复杂输入地震数据的测试结果。可以看出,对于高密集的异常振幅噪声以及高度缺失的地震道数据,本文方法仍然能实现鲁棒重建。图4(a)及图6(d)所示的f-k谱图对比表明,本文方法重建结果的高低频信息均能得到较高质量的恢复。由此可见,本文方法对于严重异常振幅噪声下的高缺失数据重构具有较强的鲁棒性。

为进一步验证本文方法的有效性和实用性,利用如图7(a)所示的某海上拖缆数据进行实际资料测试验证。在该实际资料中受海浪波动影响,约30%的检波器脱离预定位置。对于脱离预定位置的检波器,假定其采集信息缺失。除地震道缺失影响外,该拖缆数据存在明显的单道异常振幅噪声。分别对该地震数据应用基于L2范数及最大相关熵准则的重建方法进行信号恢复,恢复结果如图7(b)、(c)所示。可以看出,两种方法均可以较好地重建缺失道位置的数据,但L2范数的重建结果仍受异常振幅噪声影响明显;基于最大相关熵准则的重建方法可较好地进行异常振幅噪声压制以及缺失地震道重建。对比不同数据的f-k谱图特征可以明显看出,异常振幅噪声的存在导致L2范数重建结果的f-k谱图改善不明显,而本文方法对于异常振幅噪声的去除较彻底,可更好地恢复有效信号的频谱信息。

图7 实际地震数据测试分析Fig.7 Test and analysis of field seismic data

另外,该海上拖缆数据的深层信号能量较弱,为便于对比,图8给出了图7(a)～(c)中方框位置的信息。可以看出,涌浪的存在导致L2范数对信号的估计出现偏差,其求解结果不再是最优解,重建结果上部分弱信号缺失;本文方法重建结果中弱信号能量清晰、连续性较好,在一定程度上体现了本文方法在异常振幅噪声影响下的弱信号保护能力。

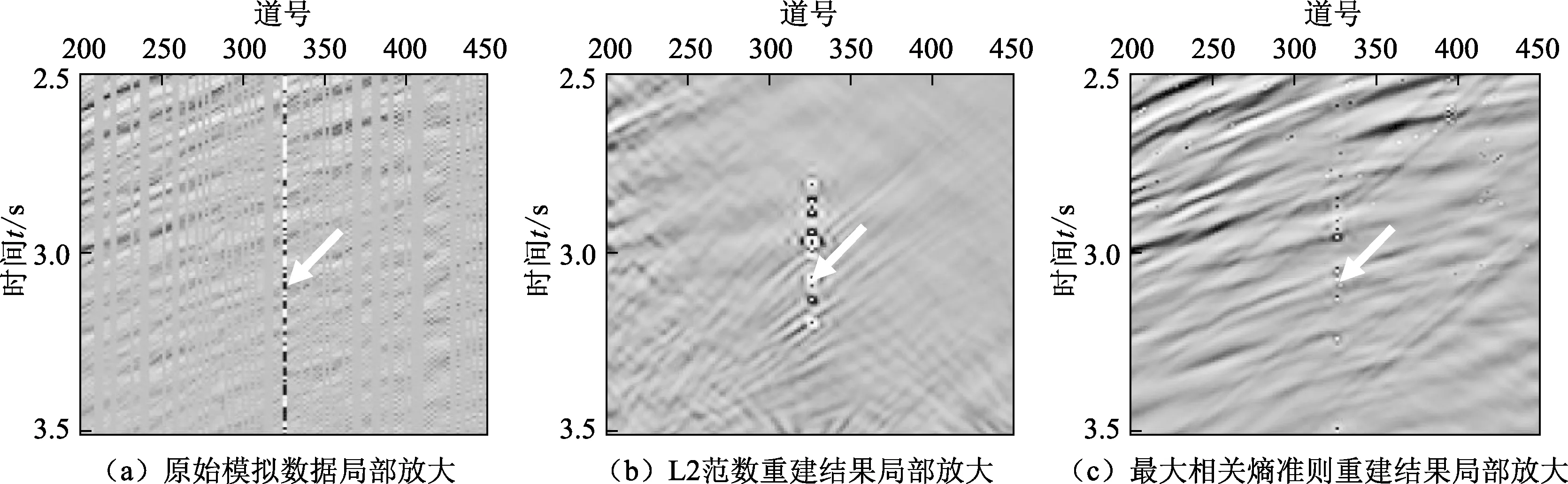
图8 实际地震数据测试局部放大Fig.8 Magnified areas of field seismic data

4 结束语

在传统压缩感知地震信号重建方法的基础上,通过引入信息论中的相关熵,构建了基于最大相关熵准则的压缩感知地震道重建方法,实现对欠采样地震记录中异常振幅噪声的有效衰减,从而保证地震道重建过程的稳定性。实验结果表明,欠采样数据中的异常振幅噪声会严重影响传统压缩感知地震信号重建方法的重建精度,而最大相关熵准则可有效抑制噪声对重建过程的影响,可有效提高重建方法的精度及稳定性,表明了本文方法在含异常振幅噪声的非规则地震道缺失重建中的准确性及有效性。