一个算术函数及其有关的恒等式

沈慧津

（西北大学数学学院，陕西西安710100）

0 引 言

设n是一个正整数，TÓTH[1]引入了模n的正则数的概念，即对任意给定的正整数模n，如果存在一个整数x，使得m2x≡m(modn)，那么，整数m被称为模n的正则数。事实上正则数的概念也是模n可乘逆的推广或延伸，因为，如果(m,n)=1，那么，其中的x就满足同余方程mx≡1(modn)。此时x就是m模n的可逆乘元！当然也存在整数m，使得(m,n)＞1 且m2x≡m(modn)。 例 如 ，取n=15,m=3，则x=2，且 32× 2≡ 3(mod 15)。容易证明整数m是模n的正则数当且仅当这里(m,n)表示m和n的最大公因子。如果正整数为模n的Hall因子，并记为d‖n。因此，整数m是模n的正则因子当且仅当(n,m)是n的Hall因子，记α(n)为模n在其完全剩余系中的所有正则数的个数，利用正则数的定义容易证明

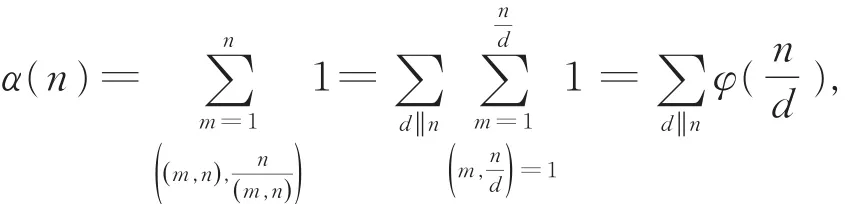
其中，φ(n)表示Euler函数，即模n的完全剩余系中与n互素的正整数的个数。

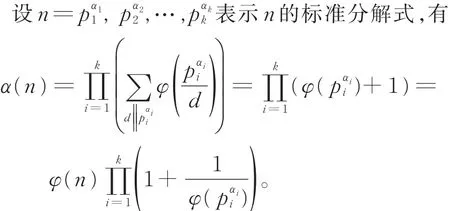
特别地，当n=p为素数时，有α(p)=p。

对任意正整数q及整数n，设A(q)表示模q在区间1≤m≤q中所有正则数的集合，显然此集合对模q的同余以及普通乘法形成一个半群！在此半群中，对任何元素m，均存在一个非零整数x，使得mx为幂等元，即对所有正整数 k有(mk)k≡mx(mod q)。如果(m,q)=1，那么m一定存在逆元；而当(m,q)＞1时，m不存在逆元。类似的代数性质很多，但这并不是本文关注的重点。现在引入新的三角和函数C*q(q)：

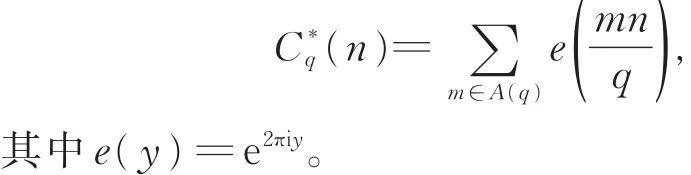
设B(q)表示区间1≤m≤q中所有与q互素的正整数集合，记

那么，称Cq(n)为Ramanujan和。对任意正整数，Ramanujan的经典结果[2]给出了恒等式

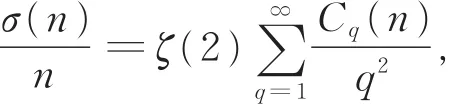
其中ζ(s)表示Riemannζ-函数，σ(n)表示n的所有因数之和。

TÓTH[3]将这一结果进行了推广，并证明了对任意正整数q1,q2,…,qk，有恒等式

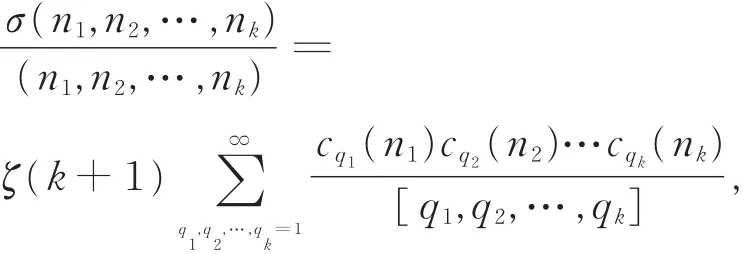
其中(n1,n2,…,nk)和[q1,q2,…,qk]分别表示整数n1,n2,…,nk的最大公约数和最小公倍数。

文献[4]也对以上结果进行了进一步推广和延伸。有关其他的和式或恒等式可见文献[5-13]，不再一一列举。

受文献[4]的启发，利用初等方法以及三角和的性质研究了无穷级数

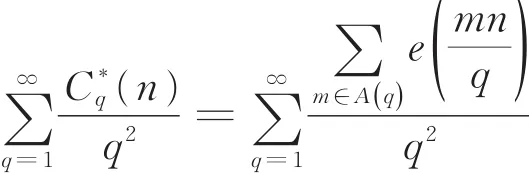
的计算问题，并得到以下2个结果。

定理1设q是任意正整数，则有恒等式

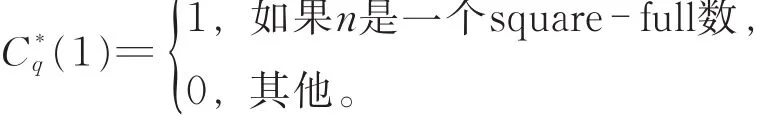
显然可用此结论来判断一个正整数q是不是square-full数（一个正整数n称为square-full数，如果p|n，则有 p2|n）。

定理2对任意正整数n，有恒等式

特别地，当n=1时，有恒等式

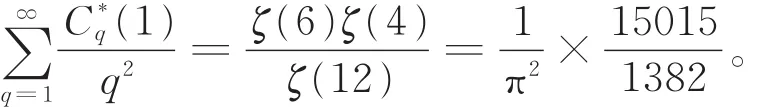
利用正则数的性质还可得到以下推论。

推论1设整数q＞1，且标准分解式为q=表示所有自然数中q的正则数的集合，则对任意实数s＞2，有

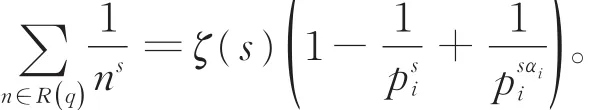
特别地，当q是一个无平方因子数时，有

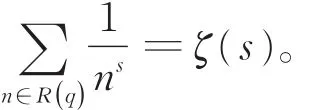
对一般的正整数q，当s=2时，有

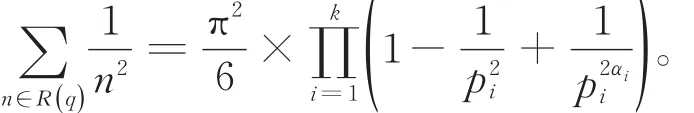
事实上，由定理2的证明过程可知，对任意整数n及实数s＞1，也可以给出Dirichlet级数的精确计算式，只是此时不一定能计算得到ζ(s)。

很显然，将本文的结果推广为文献[4]中的形式，是我们进一步研究的方向和目标！

1 若干引理

为了完成定理的证明，需要以下引理。下文中，将用到一些初等数论知识以及三角和的性质，这些内容在文献[13-15]中有详细描述，不再赘述。

引理1设n是一个给定的整数，对任意的正整数q，有恒等式

引理1得证。

引理2设k是一个给定的整数，对任意整数n，有恒等式

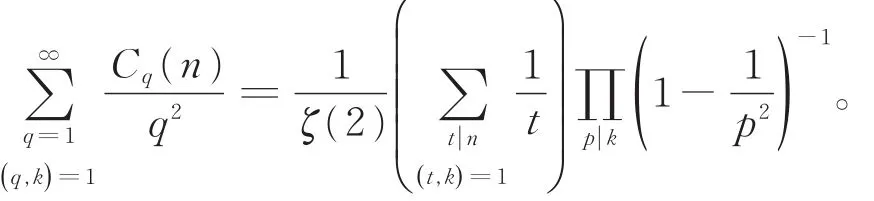
证明由Möbius函数以及三角和的性质，可得恒等式

于是应用式（1）和式（2），有

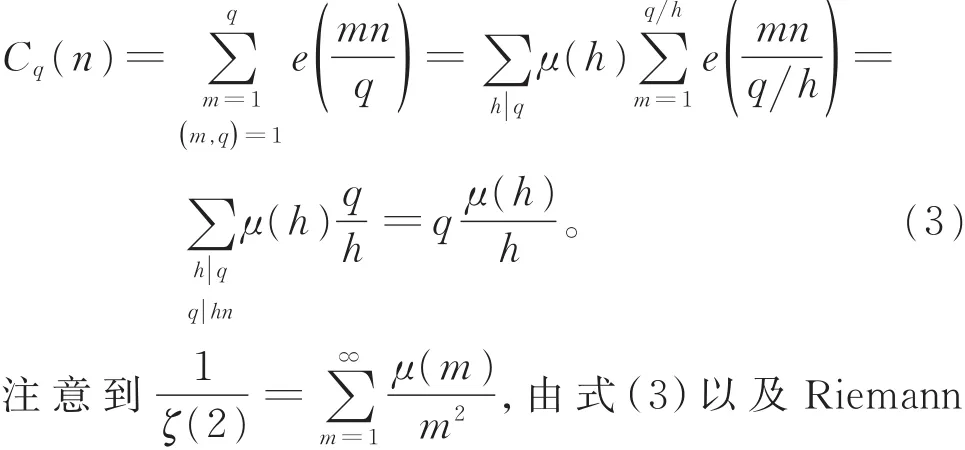
ζ-函数的定义，有

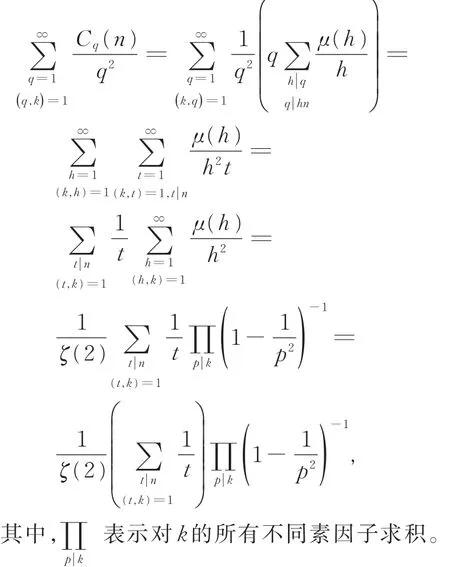
引理2得证。

2 定理的证明

先证定理1。设q和h是2个正整数且(q,h)=1，那么对任意正整数 n，有 C*qh(n)=C*q(n)C*h(n)，即C*q(n)是q的可乘函数。事实上，注意到Ramanujan和Cq(n)是q的可乘函数，由引理1，有

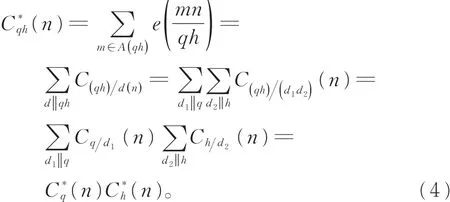
所以，为证明定理1，只需证明q=pα即可，其中p为素数，α为正整数，显然 C*1(n)=1，如果q=pα，则有

结合式（4）和式（5），定理1立刻得证。

再证定理2。对任意整数，应用引理1、引理2及Euler积公式（参见文献[1]第11章定理11.7），有恒等式

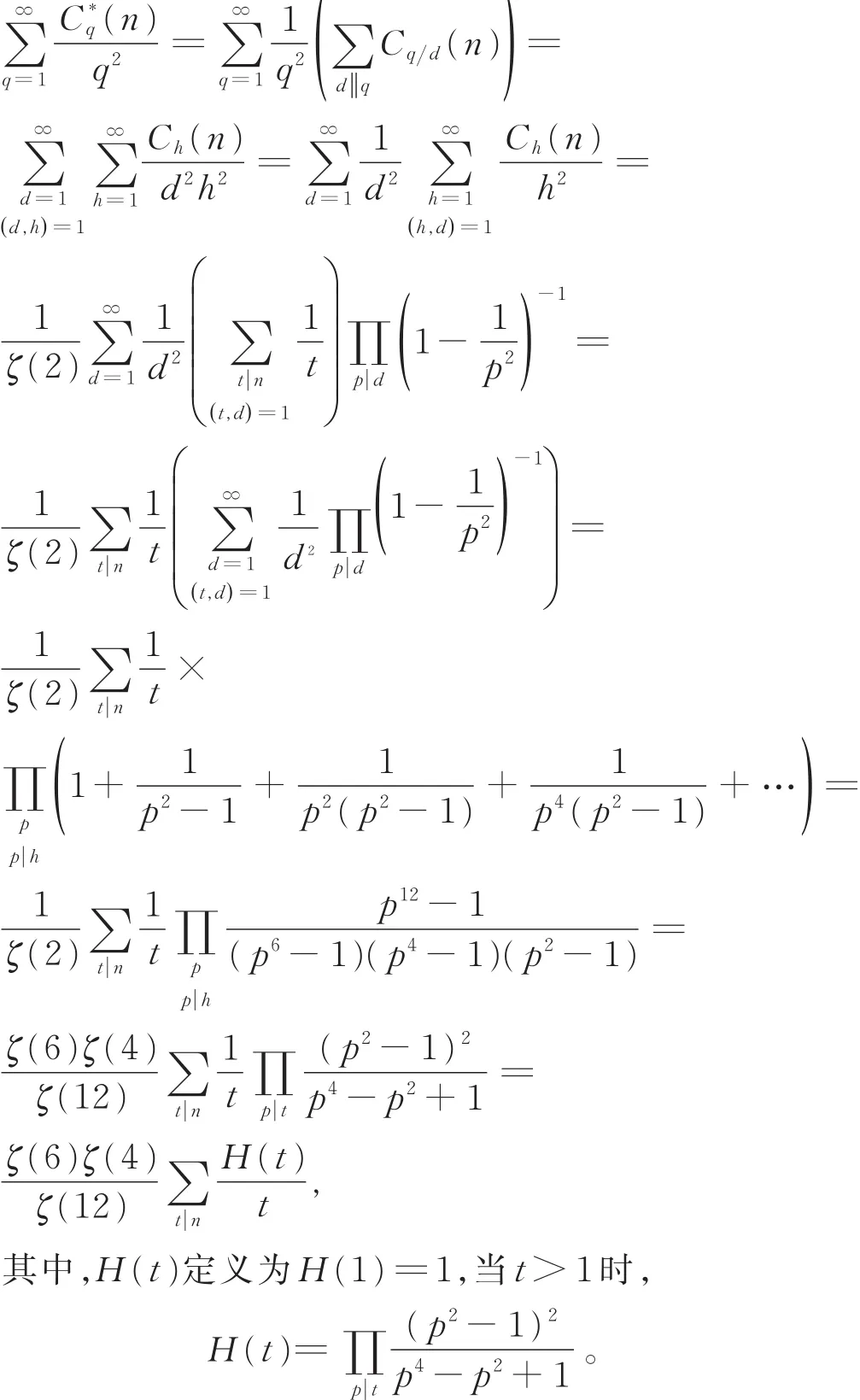
利用整数n是模q的正则数的充要条件，易得推论1（此处证略）。