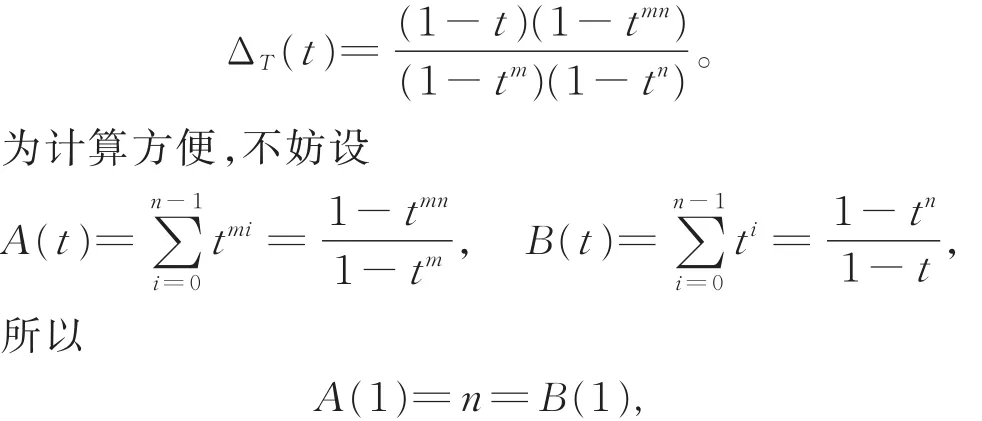纽结理论在数论中的应用

陶志雄

（浙江科技学院理学院，浙江杭州310023）

1 问题的提出

纽结理论看似与数论[1]毫不相干，但已有不少纽结方面的结果是用数论来表达的，例如文献[2]。本文将给出反向的情形，即利用纽结理论证明数论的2个结果：

定理1若m，n是互素的整数，则24整除(m2-1)(n2-1)。

定理2若m，n是互素的整数，则12整除(m-1)(n-1)(2mn-m-n-1)。

容易举例说明，若m，n不是互素，则定理就不成立。

2 定义与命题

定义1[3-5]假设K是一定向纽结，多项式∇K(t)∈ℤ[t]定义如下：

(1)若K与平凡纽结同痕，则∇K(z)=1；

(2)若3个纽结或链环仅在1个交叉处不同，而且不同处如图1所示，则

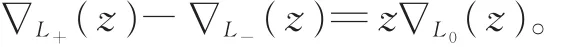
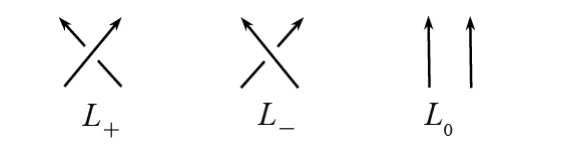
图1 L+，L-，L 0Fig.1 L+，L-，L 0

一般来说，一个有n个分支的链环的Conway多项式可表示为[6]

类似地,可定义 Alexander多项式ΔL(t)∈ℤ[t]与Conway多项式的关系为

尤其是当n=2时，a1(L)=lk(L)，或者说当L+是纽结时，

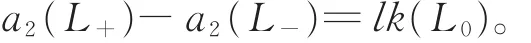
定义2[2,5,7]假设K是定向纽结，罗朗多项式VL(t)∈ℤ [t±1]定义如下：

（1）若K与平凡纽结同痕，则VK(t)=1；

（2）若3个纽结或链环仅在1个交叉处不同，而且不同处如图1所示，则

那么此多项式是一个纽结与链环不变量，称为Jones多项式。

命题1[2,5,8]设VL(t)是有c(L)个分支链环的琼斯多项式，则

3 定理的证明

定理1的证明考虑Torus纽结T＝T(m,n)(m，n互素)，其Jones多项式为[5,7]

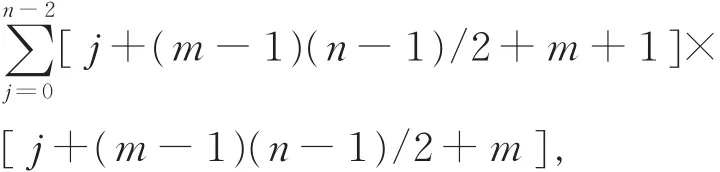
等式右边第2个∑ 中每一项可改写为

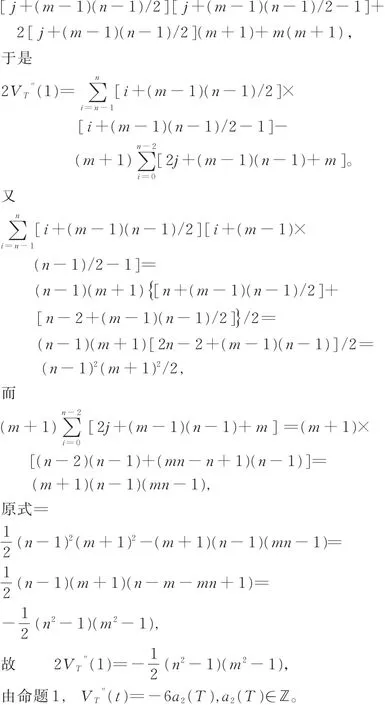
定理1得证。

定理2的证明若T＝T(m,n)(m，n互素)仍然表示Torus纽结，则其Alexander多项式为[4-5,7]