几类整循环图的秩的界

周后卿

（邵阳学院理学院，湖南邵阳422000）

0 引 言

设图G=(V,E)是具有n个顶点的简单图，V={v1,v2,…,vn}为顶点集，E为边集。设图G的邻接矩阵为A，如果图G的邻接矩阵A是奇异矩阵，则图G是奇异的。矩阵A的零空间记为ε0(A)={v0:A v0=0}，即方程组A v0=0的解向量构成的空间。G的零度，即零空间ε0(A)的维数，用η(G)表示,是矩阵A的零特征值的重数。图G的秩，用rank(G)表示，是矩阵A的秩，等于n-η(G)。图的秩是图的一个不变量，是反映图固有特性的重要概念；图的秩在物理、化学中也有应用；在控制论中，图的秩可以用来判定线性系统是可控制的还是可观察的。所以，研究图的秩具有一定的理论意义和应用价值。

国内外学者对图的零度与秩进行了一些研究。CHANG等[1-3]研究了余图的秩并探讨了具有秩为4，5的图的结构特征；CHEN[4]分析了简约单圈图的秩集；苏莉等[5]刻画了秩为2与3的带号图以及秩为4的带号二部图。本文将探讨几类整循环图的秩的界。

1 循环图的背景知识

首先给出循环图的定义：循环图G(n,S)=(V,E)的顶点集V={0,1,2,…,n-1}，n为正整数 ,S⊆{0,1,2,…,n-1}，0∉S； 边 集E={eij|i与j相邻当且仅当i-j(modn)∈S},集合S称为循环图G(n,S)的符号集。例如，循环图G(8,{2,3})是一个度为4的正则图，见图1。

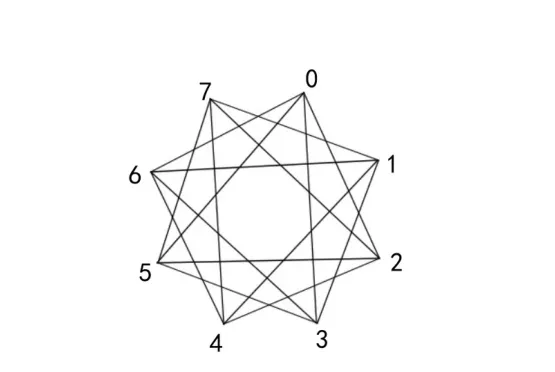
图1 具有8个顶点的循环图Fig.1 The circulant graph on 8 vertices

循环图一定是正则图，其邻接矩阵为循环矩阵。如果循环图的邻接矩阵的特征值全为整数，则称为整循环图。

循环图是一类重要的互联网络拓扑结构图,某些网状互联网络实质上就是循环图对应的网络，循环网络是双环网的自然推广,对循环图的网络应用研究已有很多。在过去几十年中,循环图与整循环图不断出现在编码理论、超大规模集成电路（VLSI)设计、Ramsey理论、并行计算和分布式计算中，在量子物理学中也有重要应用[6]。

对于循环图G(n,S)的特征值，文献[7]给出了计算公式：

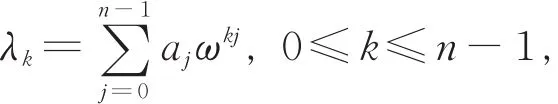
设Gn(d)={k|gcd(k,n)=d,1≤k＜n}是由小于n并且与n具有最大公约数d的所有正整数组成的集合。令D n是n的所有不超过成的集合,即1,2,…,k。

WASIN[8]证明了下列命题：

命题1一个循环图G(n,S)是整循环图当且

为了便于表述,习惯将整循环图(integral circulant graphs)记为 ICGn(D)。

对于整循环图的特征值，可以借助Ramanujan和（用R n(t)表示）来求解。

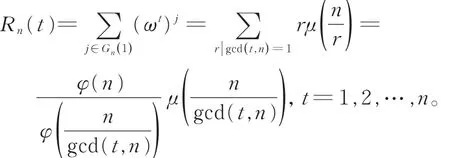
其中,φ(x)表示Euler函数,若(i=1,2,…,k)为素数，ai∈Ν(i=1,2,…,k)为p i重数,Ν表示正整数集，则

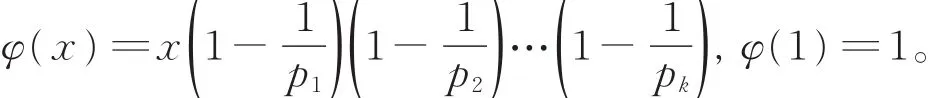
μ(x)表示莫比乌斯（Mobius）函数，具有下列性质：

(i)μ(1)=1，

(ii）当n存在平方因子时,μ(n)=0，

(iii）当n为素数或奇数个不同素数之积时,μ(n)=-1，

(iv）当n为偶数个不同素数之积时,μ(n)=1。

注意到,R n(0)=|Gn(1)|=φ(n),Rn(1)=μ(n)。对n的任意因子d以及1≤i≤n-1,都有

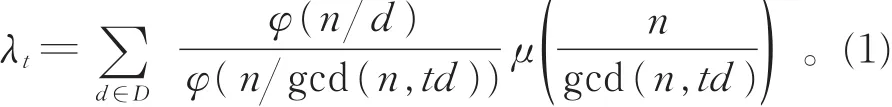
2 引理与结论

为得到本文结论,需要以下引理。

引理1[9]设n=pqm，p,q是不同的素数，且gcd(m,pq)=1。若 λi为整循环图 ICGm({1})具有重数 ti的特征值,则 -2λi,(p-2)λi,(q-2)λi和(p+q-2λi)是整循环图ICGn({p,q})分别具有重数(p-1)(q-1)ti,(q-1)ti,(p-1)ti和ti的特征值。

引理2[9]设n=pqrm,p,q,r是不同的素数,且gcd(m,pqr)=1,若 λi为整循环图 ICGm({1})具有重数 ti的特征值,则 3λi,(3-2r)λi,(3-2p)λi,(3-2q)λi，(pq-2p-2q+3)λi，(pr-2p-2r+3)λi，(qr-2q-2r+3)λi和 (pq+pr+qr-2p-2q-2r+3)λi是整循环图ICGn({p,q,r})分别具有重数(p-1)(q-1)(r-1)ti， (p-1)(q-1)ti， (q-1)(r-1)ti，(p-1)(r-1)ti，(r-1)ti，(q-1)ti，(p-1)ti和ti的特征值。

证明不失一般性,设ai∈Ν(i=1,2,…,t)，p1，p2,…,pt是不同的素数。对n的正因子d,设bi∈Ν(i=1,2,…,t)。由代数学知识可知,对任何整数a,b,c,若gcd(a,c)=1,则有gcd(ab,c)=gcd(b,c)。从而,若 gcd(n,t)=1,则 gcd(n,td)=gcd(n,d)。由此，可得到

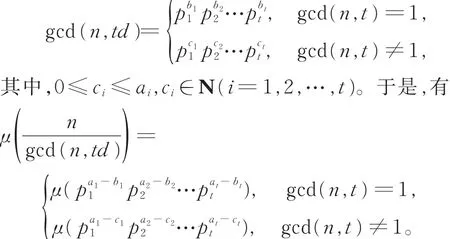
现分2种情形讨论。

情形1假设在集合{1,2,…,n-1}中有s个元素满足gcd(n,t)=1,即gcd(n,td)=gcd(n,d)。于是,

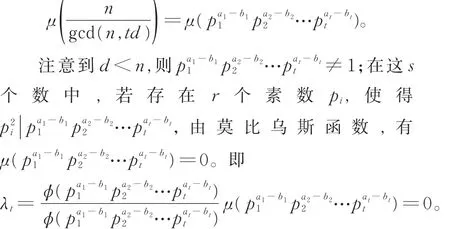
从而,推出含0的特征值有r个，因此，整循环图的秩rank(ICGn(D))=n-r。

综合上述2种情形，定理1得证。

例1设n=24，因为 D24={1,2,3,4,6,8,12}，令D={1}⊆ D24，则

那么循环图G(24,S)就是整循环图ICG24(D)。借助计算软件，可求得 G(24,S)的谱为{8,42,018,-42,-8}。从而可知该整循环图的秩为6。

再利用定理1的结果，有

其中，只有24,12,8,4含有平方因子，这样的数共有18个，所以

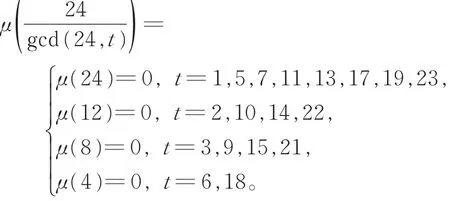
即一共有18个0特征值，6个非零特征值，从而推出循环图的秩为6。说明定理1求整循环图的秩是精确的。

定理2设n=pqm，p,q(p＜q)是不同的素数，则整循环图ICGn({ }p,q)的秩为（1） 当 p=2 时 ，rank(ICGn({ }p,q))≤n-(q-1)m；

（2）当p≠2时，rank(ICGn({ }p,q))≥2pq。

证明 由引理1，若整循环图ICGm({}1)的特征 值 为 λ0≥λ1≥…≥λm-1, 重 数 分 别 为1,t1,…,tm-1的特征值，则整循环图ICGn({ }p,q)的特 征 值 为 -2λi,(p-2)λi,(q-2)λi和 (p+q-2)λi,重数分别为 (p-1)(q-1)ti,(q-1)ti,(p-1)ti和ti。由引理1，得到整循环图ICGn({ }p,q)的图谱为

情形1当p=2时，特征值是0的个数至少为(q-1)(1+t1+t2+…+tm-1)。因为所有不同特征值的重数之和为n,即[(p-1)(q-1)+(p-1)+(q-1)+1](1+t1+t2+…+tm-1)=n，pq(1+t1+t2+…+tm-1)=n，所以，

从而推出零特征值的个数为(q-1)m。进一步可以推出整循环图ICGn({p,q})的秩为

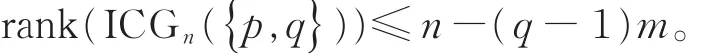
情形2若p≠2，如果整循环图ICGm({}1)的特征值中含有0特征值，不妨设λ0＞0，λm-1=-λ0＜ 0，λk=0(1≤ k≤ m-2)，则 λm-1的 重 数tm-1=1。由引理 1，得到整循环图 ICGn({p，q})的图谱为

定理得证。

例2设 n=30=2×3×5，其中，p=2,q=3,m=5。

由定理2可推出整循环图ICG30({2,3})的秩为

12≤rank(ICG30({2,3}))≤30-2×5=20 。

利用计算软件直接求此整循环图的特征值，得到的图谱为{12,4,28,010,-14,-34,-82}，从而可知整循环图的秩为20。

定理3设n=pqrm,p,q,r是不同的素数,且gcd(m,pqr)=1,则整循环图ICGn({p,q,r})的秩

rank(ICGn({p,q,r}))≥ 2pqr。

证明不妨设整循环图ICGm({1})的特征值为λ0≥ λ1≥ …≥ λm-1,重数分别为 1,t1,…,tm-1。则由引理2，整循环图ICGn({p,q,r})的图谱为

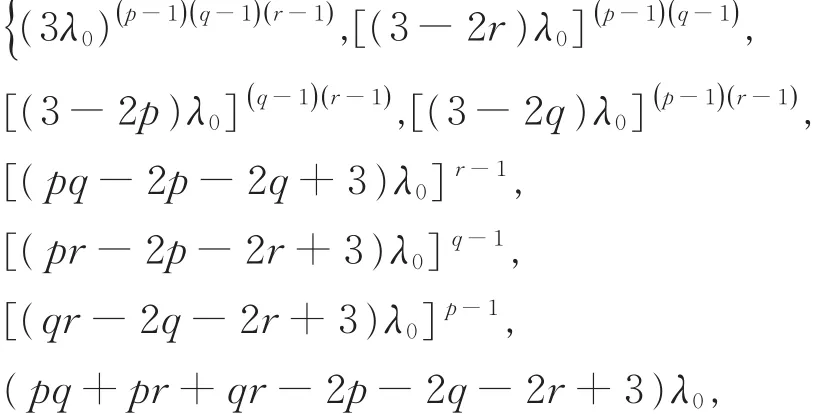
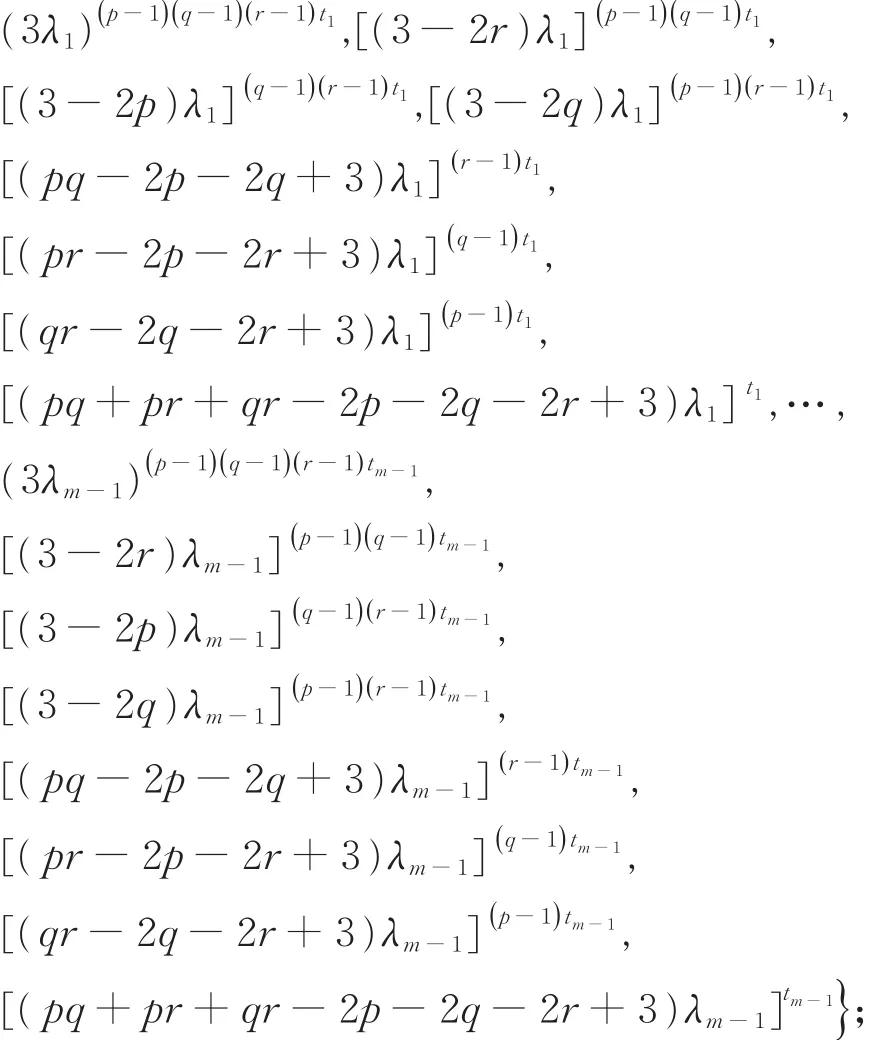
因为素数p,q,r不相等，显然，3-2r,3-2p,3-2q，pq-2p-2q+3，pr-2p-2r+3，qr-2q-2r+3，pq+pr+qr-2p-2q-2r+3不为0，因此，只需考虑 λi是否为 0。

现考虑一种极端情形，即λ0＞0。不妨设λm-1=-λ0＜ 0， λk=0(1≤ k≤ m-2)， 这 时tm-1=1，则整循环图ICGn({p,q,r})的图谱为

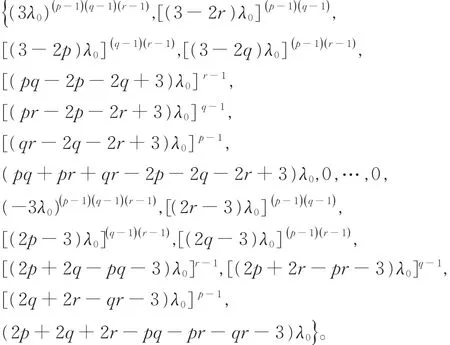
于是，可推出非零特征值的个数为

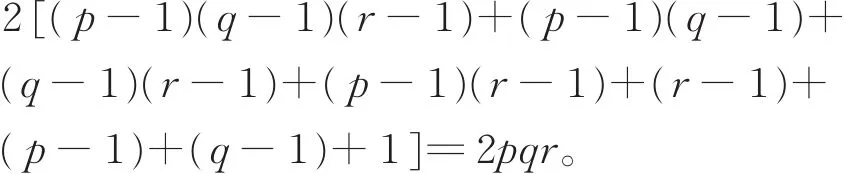
从而得到整循环图ICGn({ }p,q,r)的秩

rank(ICGn({p,q,r}))≥2pqr。

定理3证毕。